然而，随着颗粒体积分数的增大，炸药的脆性增加，更容易发生拉伸破坏。模型一、模型二和模型三的破坏应变分别为0.8%、1.3%、1.39%。图8－35三种不同颗粒体积分数和颗粒分布细观结构模型的应力－应变曲线图8－36～图8－38 所示为三种细观模型在动态拉伸载荷下的损伤破坏过程。从三种模型的计算结果可以发现，动态拉伸作用下PBX 的损伤机理主要是界面脱黏和黏结剂撕裂。......
2023-06-27
计算结果与分析的综合报告
【摘要】：为了验证黏结剂Estane 参数的有效性，首先对黏结剂在应变率分别为0.005 s－1、0.5 s－1和15 s－1的条件下进行了模拟计算，得到黏结剂在不同应变率下的应力－应变曲线，并将计算结果与实验结果［16］进行对比。图7－14黏结剂Estane 数值计算和实验结果比较为了观察黏结剂的黏弹性作用对PBX9501 力学性能的影响，分别模拟了在应变速率为0.001 1 s－1、0.011 s－1、0.11 s－1和0.44 s－1条件下的单轴压缩实验，与实验测量值进行比较。
为了验证黏结剂Estane 参数的有效性，首先对黏结剂在应变率分别为0.005 s－1、0.5 s－1和15 s－1的条件下进行了模拟计算，得到黏结剂在不同应变率下的应力－应变曲线，并将计算结果与实验结果［16］进行对比。数值计算结果和实验结果如图7－14 所示，由图中可以看出，计算结果和实验结果吻合较好。初始阶段应力会迅速增加，随后开始趋缓，这表明在小应变时，黏结剂主要表现为弹性性质，在达到一定应变后，黏结剂主要表现为黏性性质。在同等应变条件下，应力会随着应变率的增加而变大。
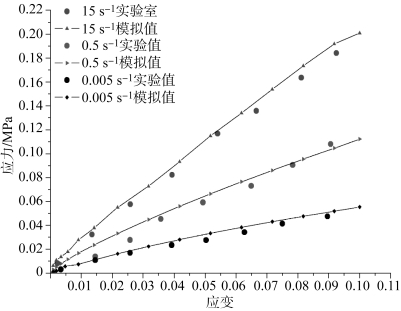
图7－14 黏结剂Estane 数值计算和实验结果比较
为了观察黏结剂的黏弹性作用对PBX9501 力学性能的影响，分别模拟了在应变速率为0.001 1 s－1、0.011 s－1、0.11 s－1和0.44 s－1条件下的单轴压缩实验，与实验测量值进行比较。图7－15 所示为基于真实细观图片模型在应变速率为0.001 1 s－1时，PBX 材料Y 方向的应力分布云图。从图中可以看出，在加载过程中，颗粒的边界尤其是大颗粒与小颗粒之间、大颗粒与边界之间会是应力相对集中的地方，而且可以发现这些应力集中区域主要是沿Y 方向分布的，这和模型的加载方式是相关的。
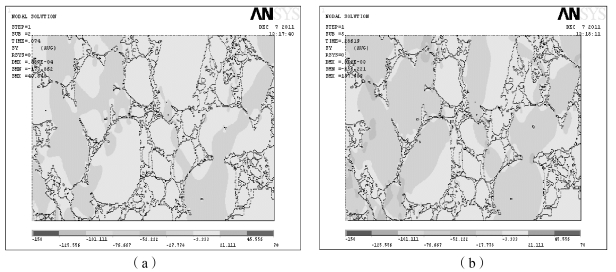
图7－15 应变速率为0.001 1 s 时PBX 材料Y 方向上的应力分布图
（a）载荷步一；（b）载荷步五
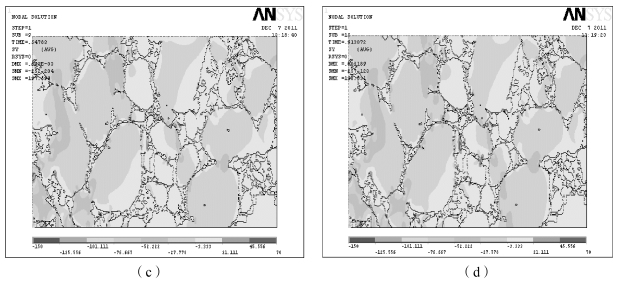
图7－15 应变速率为0.001 1 s 时PBX 材料Y 方向上的应力分布图（续）
（c）载荷步九；（d）载荷步十五
图7－16 所示为基于真实细观图片模型与颗粒体积分数为95%的六边形分布模型在不同应变速率下的应力－应变曲线，由图中可以看出，PBX 9501有效弹性模量受应变速率影响较大，应变率越高，PBX 9501 有效弹性模量就越大。在单轴压缩初始阶段，应力上升速度较快，应力－应变呈线性关系，PBX9501 表现为弹性性质，到达一定应变后，受到黏结剂黏性性质影响，PBX9501 开始表现为黏性性质，应力上升速度减缓。
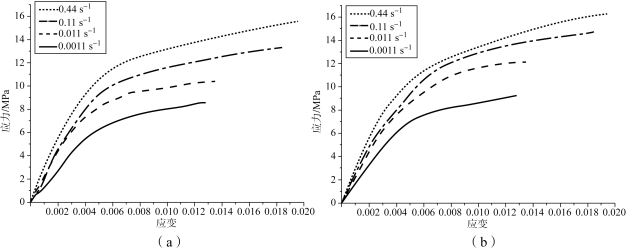
图7－16 基于真实细观模型颗粒体积分数95%的六边形分布模型在不同应变速率下的应力－应变曲线
（a）真实细观模型；（b）六边形分布模型
图7－17 所示为基于真实细观模型与颗粒体积分数为95%六边形模型在不同应变速率条件下模拟值与实验值对比。从图7－17 （a）～（d）中可以明显地看出，基于真实细观结构的有限元模型得到的结果，在初始线性阶段，与实验结果吻合很好。但是，当应变大于0.004 后，模拟结果会略小于实验结果，这是因为模型中的颗粒体积分数要比真实炸药的颗粒体积分数低。颗粒体积分数为95%的模型得到的结果要高于真实细观结构的模型，这说明炸药颗粒的体积分数及颗粒的形貌和分布方式对黏弹性力学性能有一定的影响。由图中可以看出，数值模拟结果与实验测量值吻合得较好，该模型可以用来预测炸药的力学性能。虽然黏结剂在炸药中的体积分数比较低，但是它的作用是非常明显的。在实际情况中，黏结剂的黏性可以钝化炸药的敏感性，使炸药更加安全可靠。
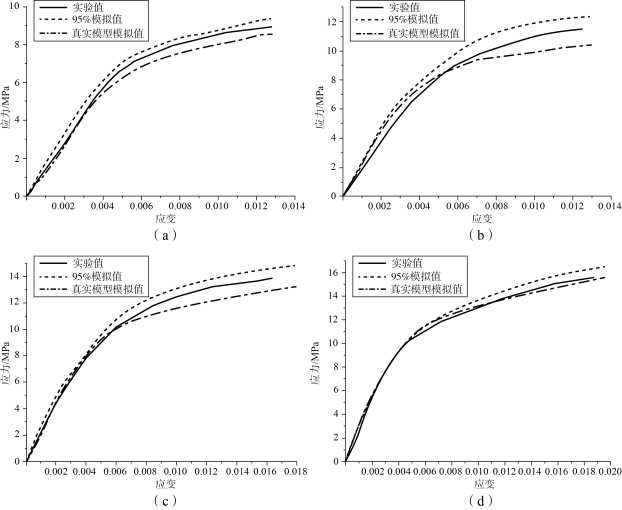
图7－17 基于真实细观模型与颗粒体积分数为95%六边形模型在应变率为0.001 1 s－1、0.011 s－1、0.11 s－1和0.44 s－1时的模拟值与实验值
（a）0.001 1 s－1；（b）0.011 s－1；（c）0.11 s－1；（d）0.44 s－1
有关高聚物黏结炸药损伤断裂的数值模拟的文章
- 详细阅读
-
电梯振动与噪声的综合分析详细阅读
电磁噪声与槽的配合、槽的斜度及电动机结构的刚度均有密切关系。（二）电梯振动与噪声引起电梯抖动、振动与噪声的主要原因如下。在降振、隔振中降低噪声。经过隔振处理后，振动级由原来的84dB可下降至75dB，机房室内噪声可由42dB下降到35dB。如果电梯有高频振动和共振现象，则要消除共振，才能消除噪声。......
2023-06-15
-
单轴拉伸计算结果分析详细阅读
我们注意到，单轴拉伸下的失效应变仅为0.004 1，说明PBX 9501 是一种脆性材料。图8－20应变率为10－3s－1时的单轴拉伸应力－应变曲线图8－21 所示为应变为0.16%、0.41%、0.45%和0.5% 时的Y 方向应变云图和损伤断裂演化图。从图中可以看出，整个拉伸过程黏结剂承受了大部分的变形。该结果表明PBX 9501 的拉伸力学性能与界面黏结强度有关，而失效路径与界面强度无关。......
2023-06-27
-
交流耐压的综合分析与判断技巧详细阅读
根据综合分析，一般可对设备作出下述判断结论：耐压合格、耐压不合格和耐压有局部缺陷。应当指出，有的设备即使通过了耐压试验，也不一定说明设备毫无问题，如电机、变压器及其他有线圈的设备，即使进行了交流耐压试验，也往往不能检出匝间、层间等缺陷，所以必须会同其他试验项目所得的结果进行综合判断。因此在同设备不同相别做交流耐压试验时，电流表的指示应基本相同。......
2023-06-27
-
信息综合分析与智能告警的优化技巧详细阅读
收集开关变位上送的带时标的 SOE 信息，形成详细的一次设备信息报告。3）综合推理以实时告警触发为起点，通过变电站逻辑推理模型，综合知识库及当前监控系统的运行环境，进行故障推理，获得对该事件的认识及可能产生的影响，从而生成故障诊断事件（报告）、故障处理报告，为实现运行设备的早期故障预警、事故的快速诊断及故障后处理等功能提供依据。......
2023-06-28
-
分析与综合：设计思维的种子详细阅读
分析与综合设计师喜欢抱怨“功能蔓延”，即那些不必要功能的增生，它们会增加费用，并把原本简单的产品变得很复杂。不过，我需要将另外两个术语引入讨论中：分析和综合，这是发散式思维和汇聚式思维的天然补充。分析与综合同等重要，而且在创造选项和做出抉择的过程中，二者都扮演着重要的角色。这些是设计思维的种子——一方面在发散过程和汇聚过程之间变动，另一方面又在分析与综合之间不断变动。......
2023-12-06
-
计算结果和分析-多尺度模拟与分析研究详细阅读
作为展示，图6.10和图6.11给出了其中尺寸为H＝50mm和H＝200mm的试样的模拟结果。对图6.12中的荷载－跨中位移计算结果进行处理，得到不同尺寸下混凝土梁的跨中最大应力（强度）和相对挠度的关系曲线如图6.13所示。表6.1梁跨中名义强度与断裂能的尺寸效应有关混凝土梁损伤演化分析的更多结果及其分析，有兴趣的读者可参阅参考文献［26］中的相关章节。......
2023-08-26
-
上海法院调研报告：网瘾少年犯罪的综合治理详细阅读
警惕网瘾之患重在综合治理——上海市第一中级人民法院关于网瘾少年犯罪的调研报告课题组成员/王列宾胡天和邱阳戎顾苹洲［2012年1月12日第8版］未成年人涉染网瘾较为普遍。2008年至2010年6月底，上海市第一中级人民法院少年庭共审理未成年人刑事案件241件，涉未成年被告人441人。(二)网瘾对未成年人犯罪的影响上述因受网络不良影响而失足的319名未成年被告人，其犯罪行为大多以侵犯他人财产、人身，满足私欲为目的。......
2024-01-19
相关推荐