首页理论教育材料本构模型的优化方法

材料本构模型的优化方法

2023-06-27 理论教育版权反馈

【摘要】：炸药颗粒采用各向同性的弹塑性本构模型。式是根据松弛条件本构方程，通过将一点的应变分解为应变球张量和应变斜张量两部分推导得到的。用Prony 级数表示黏弹性属性的基本形式为式中：和Gi为剪切模量；和Ki为体积模量；和为各Prony 级数分量的松弛时间。表7－7剪切松弛模量与松弛时间的关系

炸药颗粒采用各向同性的弹塑性本构模型。弹塑性本构采用塑性随动硬化材料模型进行描述，应变率采用Comper－Symonds 模型考虑，屈服应力和应变率的关系式为

式中：σ 为屈服应力；为应变速率；为失效应变；σ0为材料的静态屈服应力；C、p 为应变速率参数，表征材料率敏感特征；Ep为材料的塑性硬化模量；β 为参数。炸药颗粒采用HMX，弹性模量为15.3 GPa，屈服应力为230 MPa。

黏结剂采用Prony 级数形式的黏弹性本构模型，各向同性的黏弹性本构方程可以表示为

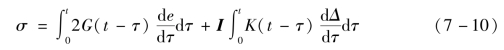
pagenumber_ebook=174,pagenumber_book=154

式中：σ 为Cauchy 应力；G（t）为剪切松弛核函数；K（t）为体积松弛核函数；e 为应变偏量部分，即剪切变形；Δ 为应变体积部分，即体积变形；t 为当前时间；τ 为过去时间；I 为单位张量。

式（7－10）是根据松弛条件本构方程，通过将一点的应变分解为应变球张量（体积变形）和应变斜张量（剪切变形）两部分推导得到的。

用Prony 级数表示黏弹性属性的基本形式为

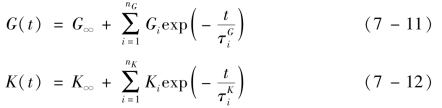
pagenumber_ebook=174,pagenumber_book=154

式中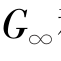： pagenumber_ebook=174,pagenumber_book=154 和Gi为剪切模量；和Ki为体积模量；和为各Prony 级数分量的松弛时间（Relative Time）。

定义下面的相对剪切模量与体积模量（Relative Modulus），即

pagenumber_ebook=174,pagenumber_book=154

式中：G0、K0分别为黏弹性材质的瞬态模量，并定义如下：

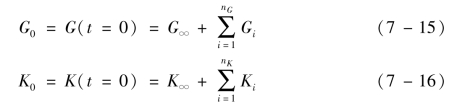
pagenumber_ebook=174,pagenumber_book=154

在ANSYS 中，Prony 级数的阶数nG和nK可以不相等，其中的松弛时间和也不必相同。对于黏弹性问题，黏弹体的泊松比一般取为时间的函数μ＝μ（t）。不过，有时情况允许也可近似设为常数，这时根据弹性常数关系，有

pagenumber_ebook=174,pagenumber_book=154

式中：E（t）为松弛模量，由实验确定。E（t）、G（t）、K（t）的相应系数比相同，这样就可以将G（t）和K（t）统一为E（t）形式。

若将松弛模量表示为Prony 级数形式，即

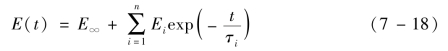
pagenumber_ebook=174,pagenumber_book=154

于是，G（t）和K（t）中有，n＝nG＝nK，（Relative Time），（Rela⁃tive Modulus）。类｀似于G0、K0，也可以同样定义瞬态松弛模量，即

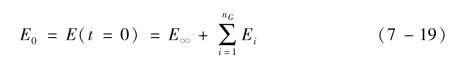
pagenumber_ebook=175,pagenumber_book=155

由式（7－17）可得

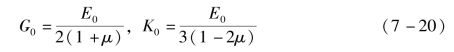
pagenumber_ebook=175,pagenumber_book=155

根据Mas 和Clements 的实验数据，可以认为黏结剂的体积模量Kb＝3.65 GPa，因此剪切模量同松弛模量存在一定的关系，即

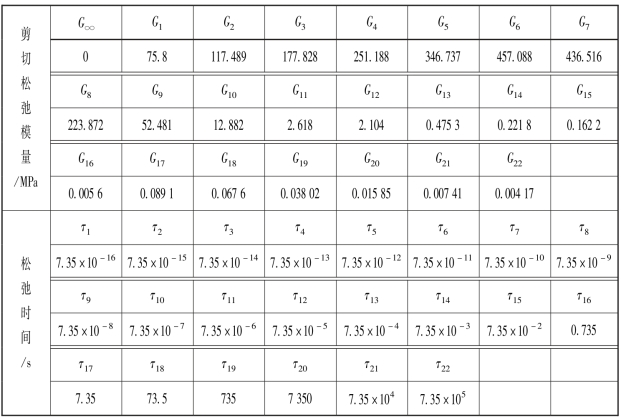
表7－7 所示为Estane 黏弹性本构参数［15］。

表7－7　剪切松弛模量与松弛时间的关系

pagenumber_ebook=175,pagenumber_book=155