研究PBX 损伤断裂的实验方法主要包括材料实验机、霍布金森杆、落锤、气炮等[1~3]。近年来,数字图像相关技术已广泛应用于研究PBX 宏细观变形破坏行为及损伤破坏机理。Zhou 等[11]结合巴西实验、轴向压缩、三点弯曲、半圆盘弯曲和Punch Loading 等准静态实验,应用DIC 方法研究了PBX 模拟材料的宏观变形破坏行为和力学性能,并建立了测量PBX 脆性材料拉伸力学性能和断裂性能的方法,测量得到PBX 的抗拉强度、失效应变以及断裂韧性等参数。......
2023-06-27
应用ANSYS 软件中结构静力学分析。它不仅可以进行线性分析,而且可以进行非线性分析,如塑性、蠕变、松弛、大变形、大应变和接触分析等。在ANSYS 中,计算流程可以归纳为以下几个部分。
(1)定义单元类型。选用的单元类型分别为二维结构实体单元PLANE183和PLANE182。在模型中,分别用圆形和六边形的规则形状来代表炸药颗粒。因此,选用8 节点的PLANE183。由于黏结剂形状不规则,选用4 节点的PLANE182,这样便于后面的网格划分。
(2)定义材料属性。采用ANSYS 材料模型库中提供的材料模型和参数属性。主要应用的是线弹性材料模型、非线性弹性模型和黏弹性模型。其中,非线性弹性模型采用各项等向强化的Mises 率不相关塑性Bilinear 模型,黏弹性模型采用Prony 中Shear Response 模型。
(3)建立实体模型。采用几何模型网格划分法对PBX 材料进行了随机细观和真实细观结构两种方式的建模。其中,随机细观模型的建立是通过MAT⁃LAB 软件编程实现的。真实细观模型的建立是通过扫面电镜获得清晰图片,再通过相关软件进行数字离散化提取后得到的。
(4)划分有限元网格。针对两种模型分别采用了不同的网格划分。对于随机细观模型,因其颗粒是规则形状的,所以采用单元尺寸控制法对其进行网格划分,这样可以较为准确地捕捉到场量的分布和梯度的变化,尤其是应力/应变的分布。同时,在应力集中的位置可以根据需要画出相对密集的单元网格,这样可以捕捉到塑性区域的产生位置、扩展过程以及最终塑性区域的大小。对于真实细观模型,因为在建模时对图片采用了数字离散化,形成的是若干个像素点单元,而不是以线或面的形式存在。因此,可以直接采用均匀网格划分,这样产生的网格数目很大,不用再在应力集中的位置进行细化网格。
(5)设定边界条件。这里是针对周期性模型进行数值模拟分析的,所以需要施加循环对称约束条件,以此保证截面始终保持原始形状。
(6)定义分析类型和选项。在针对弹性结构进行模拟时,不用设置时间步长,可以直接计算到最后的结果。在针对弹塑性和黏弹性结构进行模拟时,一定要注意缓慢加载,使用小的时间步长,这样既可以保证在每一个时间步内最大的应变增量小于5%,又可以加强收敛,增加模拟计算结果的准确性。
(7)导出所需数据、图形等文件。
在PBX 的细观模型上,通过施加边界条件来计算得到炸药的宏观有效力学性质。为了保持边界节点的位移与边界面平行,需要满足下面的耦合关系[14],即
![]()
式中:ui和uj分别为位移边界面平行于i 和j 的边界节点。
计算中施加的周期性边界和位移载荷如图7-4 所示,即在该模型的上边界和右边界进行耦合约束,左边界和下边界分别固定,以此保证模型在变形后,截面形状保持不变。同时,在该模型的上边界施加应变为0.01 的压缩位移载荷模拟单轴压缩试验。在二维分析中运用平面应变假设,空间内各个方向上的平均应力和平均应变为

式中:i 表示应力/应变张量的方向;V 表示代表体积单元的体积。
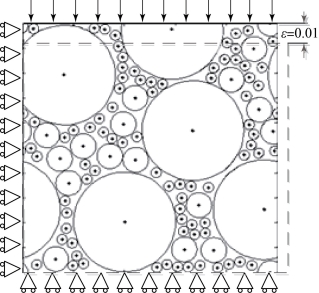
图7-4 载荷及边界条件施加方式示意图
根据二维应力-应变关系,有
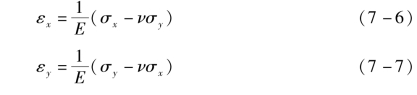
从而可以得到PBX 有效弹性模量为

式中:σx和σy分别为x、y 方向的应力;εx和εy分别为x、y 方向的应变;ν为泊松比;E 为有效弹性模量。
计算中炸药颗粒和黏结剂均采用各向同性的弹性本构模型。材料参数如表7-1 和表7-2 所示。
表7-1 炸药颗粒的弹性模量
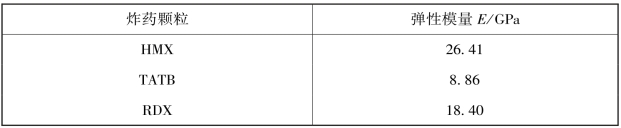
表7-2 黏结剂的弹性模量

有关高聚物黏结炸药损伤断裂的数值模拟的文章

研究PBX 损伤断裂的实验方法主要包括材料实验机、霍布金森杆、落锤、气炮等[1~3]。近年来,数字图像相关技术已广泛应用于研究PBX 宏细观变形破坏行为及损伤破坏机理。Zhou 等[11]结合巴西实验、轴向压缩、三点弯曲、半圆盘弯曲和Punch Loading 等准静态实验,应用DIC 方法研究了PBX 模拟材料的宏观变形破坏行为和力学性能,并建立了测量PBX 脆性材料拉伸力学性能和断裂性能的方法,测量得到PBX 的抗拉强度、失效应变以及断裂韧性等参数。......
2023-06-27

PBX 对外载作用下的响应非常复杂,连续介质损伤力学模型和微裂纹细观损伤模型这两类损伤模型广泛用来研究PBX 在外载作用下的损伤破坏。Browning 等[31]针对PBX9501 和PBX9502 提出了一维黏塑性损伤本构模型,认为塑性由材料内部损伤引起,本构方程参数由蠕变实验及循环加卸载实验得到,但该模型还不能很好地模拟长时间条件下的应力松弛。丁雁生等[32]采用一维黏弹性蠕变损伤模型对PBX 的蠕变损伤及破坏进行了研究,损伤演化由应变控制。......
2023-06-27

食物中的维生素C一旦被人体小肠上段吸收,就分布到体内所有的水溶性结构中。正常成人体内的维生素C代谢活性池中约有1500mg维生素C,最高储存峰值为3000mg维生素。人体内维生素C的缺乏会导致坏血病。富含维生素C的食物有花菜、青辣椒、橙子、葡萄汁、西红柿等。随着维生素C制剂的应用日益广泛,简便地预测维生素C药物的稳定性就显得尤为重要。利用这一水解反应来测定维生素C在酸性溶液中变成多羟基酸的动力学性质。......
2023-12-04

纳米粒子体积小,所包含的原子数很少,相应的质量也极小,因此许多现象不能用包含有无限个原子的块状物质的性质进行说明。但大量的实验观察和理论论证发现,纳米粒子的熔点会下降,尤其是处于纳米尺度的粒子的熔点会大大低于其块体材料。......
2023-06-20

表13材料的比强度1.3.2弹性与塑性材料在外力作用下产生变形,当外力去除后,能完全恢复到原始形状的性质,称为弹性,这种可恢复的变形称弹性变形。......
2023-12-02

算术平均数可根据样本大小及分组情况而采用直接法或加权法计算。计算若干个来自同一总体的样本平均数的平均数时,如果样本含量不等,也应采用加权法计算。3.平均数的基本性质。用几何平均数比用算术平均数更能代表其平均水平。......
2023-11-17

表4-7三轴实验的结果从上表可以看出,煤岩的抗压强度C0只有10.8MPa,模量比大于500,所以煤岩属于高模量比、极低强度岩块,其弹性(杨氏)模量E较常规的砂岩杨氏模量要小,只有12282.7MPa,易形成较宽的水力裂缝,同时煤层具有高滤失性,这就决定了在煤层中造长缝是比较困难的。图4-12、图4-13反映了煤岩受应力变化而发生应变的情况。......
2023-11-18

所以,与纳米结合的陶瓷,原子的结构性能变强,韧性也变大,使新诞生的陶瓷材料具有神奇的力学性质。近年来科学界一直在倡导一种叫纳米技术的新技术,运用纳米来为人类生活服务的一项新的科学产业。电子决定了一个元素的化学性质,并且对原子的磁性有很大的影响。......
2024-07-20
相关推荐