因此，泰森多边形具有随机或特定分布的特点，适合于PBX 的细观结构建模［4～6］。图8－1Voronoi 图及算法Voronoi 图；Voronoi 算法PBX 9501 的细观结构由HMX 颗粒和典型黏结剂材料Estane 5703 组成。PBX 9501 的细观结构尺寸为1 mm×0.8 mm，由98 个颗粒组成，粒径分布为25～98 μm，黏结剂宽度为8 μm，HMX 和Estane 5703的密度分别为1.58 g／cm3和0.9 g／cm3。......
2023-06-27
随机分布规则下的颗粒细观结构模型
【摘要】：应用MATLAB 程序编写完成了炸药颗粒圆形随机分布模型，图7－1 所示为炸药颗粒体积分数分别为30%～80%的细观模型。该程序的主要思想是在一定区域内，随机生成若干个数组作为圆心的坐标，而圆形的半径是自由设定的，由此生成若干随机圆形，以此代表炸药颗粒。将这些命令流直接复制粘贴到ANSYS 的命令行中即可完成模型的建立。因此，为了提高炸药颗粒体积分数，更好地模拟真实PBX 的有效力学性能，建立了炸药颗粒六边形规则分布模型。
应用MATLAB 程序编写完成了炸药颗粒圆形随机分布模型，图7－1 所示为炸药颗粒体积分数分别为30%～80%的细观模型（其中颗粒体积分数为70%的模型有三个，采用的是不同颗粒级配和不同分布方式）。该程序的主要思想是在一定区域内，随机生成若干个数组作为圆心的坐标，而圆形的半径是自由设定的，由此生成若干随机圆形，以此代表炸药颗粒。此模型中的随机圆是相互不重合的，在边界处具有周期连续性。
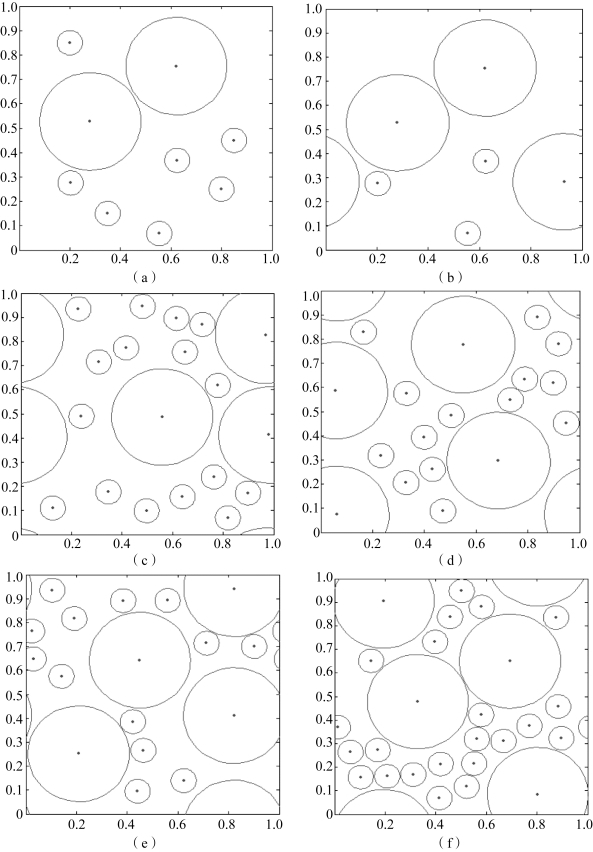
图7－1 不同体积分数的圆形颗粒随机分布几何模型
（a）颗粒体积分数为30%；（b）颗粒体积分数为40%；（c）颗粒体积分数为50%；（d）颗粒体积分数为55%；（e）颗粒体积分数为60%；（f）颗粒体积分数为65%；
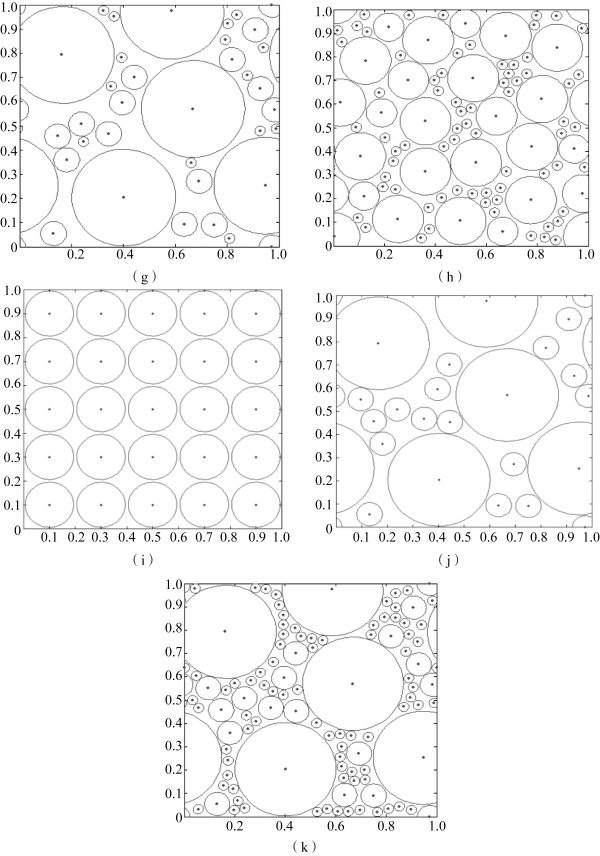
图7－1 不同体积分数的圆形颗粒随机分布几何模型（续）
（g）颗粒体积分数为70% （1）；（h）颗粒体积分数为70% （2）；（i）颗粒体积分数为70% （3）；（j）颗粒体积分数为75%；（k）颗粒体积分数为80%
为了方便在ANSYS 中进行建模，在数据导出时，编写相关程序，使得MATLAB 自动生成APDL 命令流如下：
／prep7
RECTNG，0，1，0，1，
cyl4，0.587375，0.976204，0.2
cyl4，0.163693，0.792678，0.2
cyl4，1.16369，0.792678，0.2
cyl4，0.692848，0.270401，0.05
cyl4，0.181311，0.359301，0.05
cyl4，0.984795，0.565351，0.05
cyl4，－0.0152052，0.565351，0.05
cyl4，0.878105，0.707692，0.02
cyl4，0.353214，0.663653，0.02
cyl4，0.246455，0.433887，0.02
cyl4，0.393299，0.781715，0.02
……
将这些命令流直接复制粘贴到ANSYS 的命令行中即可完成模型的建立。
因为在真实PBX 中，炸药颗粒的体积分数通常是很高的，可达90%以上，而圆形随机分布方式很难达到这么高的体积分数。因此，为了提高炸药颗粒体积分数，更好地模拟真实PBX 的有效力学性能，建立了炸药颗粒六边形规则分布模型。图7－2 所示为颗粒体积分数分别为30%、50%、80%和97.5%的PBX 模型。
图7－2 不同体积分数的六边形颗粒几何模型
（a）颗粒体积分数为30%；（b）颗粒体积分数为50%；（c）颗粒体积分数为80%；（d）颗粒体积分数为97.5%
有关高聚物黏结炸药损伤断裂的数值模拟的文章
- 详细阅读
-
真实结构细观模型优化探讨详细阅读
对PBX 表面进行打磨、抛光、喷金等处理后，利用SEM 装置即可得到PBX 的细观结构照片。然而，SEM 照片是PBX 局部位置放大的物理图像文件，就其自然格式而言，计算机中的物理图像文件是不能直接用来处理的，必须先对它进行数字图像处理。如图7－3 所示的PBX 炸药颗粒呈黑色，黑色的灰度值比较低；而黏结剂呈灰白色，所属的灰度值比较高。真实结构的颗粒体积分数为90%。图7－3PBX 炸药的SEM 图与有限元网格模型SEM 图片；有限元网格模型......
2023-06-27
-
混凝土细观模型建立方法，基于材料细观构造图像详细阅读
为了真实描述混凝土内部的细观构造，细观尺度下的混凝土模型须基于材料细观构造图像来构造和建立。这里基于图像重构混凝土细观有限元模型的方法可以概述为：首先将混凝土的细观图像转为由具有不同灰度值的像素点构成的灰度图像，如图6.27所示。图6.27基于图像的混凝土细观模型建立方法示意图众所周知，混凝土中骨料与基体之间的界面层是易于损伤演化的薄弱层，对混凝土损伤演化及宏观力学性能的影响很大。......
2023-08-26
-
极限条件下的颗粒相模型优化详细阅读
若颗粒碰撞效应不占优势，相应的本构关系可以简化为:4.粒间碰撞可以忽略在一般条件下的本构关系中，参数ζτp反映了粒间碰撞对颗粒相应力和脉动能传导通量的影响。......
2023-06-22
-
宏细观损伤与结构响应的分析分析详细阅读
图2.38各焊接试样损伤演化过程宏细观关联性对比图2.39试样中的微孔洞和微裂纹演化过程以上分析表明，焊接构件内部缺陷的体积、类型、分布及其演化过程都在一定程度上影响了构件的延性损伤演化过程，微裂纹的演化是导致焊接构件卸载弹模迅速折减的主要因素，均匀分布的微孔洞和微裂纹之间的相互作用较易导致构件萌生宏观主裂纹并迅速发生断裂。......
2023-08-26
-
钢筋混凝土拉拔构件细观损伤分析模型详细阅读
图6.17钢筋混凝土拉拔试样损伤分析的细观模型钢筋混凝土粘结性能的劣化主要是粘结界面区的缺陷及混凝土的细观结构弱化导致的，在界面区的细观模拟中，钢筋采用线性弹性本构关系，砂浆与粗骨料采用含损伤后的混凝土本构关系。如图6.18所示的弹性损伤本构关系模型可表示为：式中，Em与Ea分别为砂浆与粗骨料的初始弹性模量。......
2023-08-26
-
威布尔随机分布解析详细阅读
为了考虑PBX 参数的非均匀性，引入威布尔概率分布，实现各单元材料属性随机力学参数赋值。为了清晰地描述PBX 材料破坏损伤过程，对弹性模量、泊松比、拉伸强度、断裂能等参数进行威布尔概率统计分析，在巴西圆盘实验的有限元计算中得到应用。图4－11威布尔随机数的分布函数图4－12巴西实验有限元模型......
2023-06-27
-
随机森林模型的原理详解详细阅读
另外，随机森林法可以评价各种指标的重要程度。装袋算法通过自助抽样法有效地提高了随机森林算法的准确度。Breiman在1984年提出的分类回归树是一种不稳定的学习算法，因此CART方法与装袋算法结合就形成了随机森林算法，可以提高模型预测准确率。随机森林模型中某一特征的重要性，是所有决策树得到的该特征重要性的平均值。......
2023-06-15
相关推荐