2020年，青铜峡市库区湿地保护管理局完善防火联防联控机制建设，组织保护区相邻单位参与库区防火工作，建立库区警务室，实现资源管护执法力量全覆盖。2020年，青铜峡市库区湿地保护管理局对生态环境部反馈的人类活动变化点位开展实地核查排查和处理。2020年，青铜峡市库区湿地保护管理局签订补偿协议214户，占退耕总户数的100%，完成120594.53亩的退补任务，保护区养殖企业以及人类活动全部退出，退耕区域自然生态恢复良好。......
2023-08-07
探究模拟实验的成果与分析
【摘要】：在加载直径方向拉应力最大达到抗拉强度6 MPa，由于标准巴西实验中圆盘上下两端压应力集中严重，最大压应力达到105.5 MPa。图6－13 所示为三种加载方式下圆盘开裂时刻的von Mises 应力场分布，结果表明，应力沿圆盘中心轴均匀对称分布，在圆盘上、下接触位置均出现压应力集中区域。计算结果表明，改变加载形式对应力集中有着明显的改善。
图6－9 所示为计算及测量得到的圆盘在破坏时刻的水平方向全场位移分布，结果表明，圆盘以加载轴线为中心对称向两边运动，计算和实验测量得到的水平位移场分别为0.012 mm 和0.015 mm，计算和测得的位移场分布较为一致。根据式（6－22）和式（6－23）计算得到标准巴西圆盘实验中圆盘竖直直径上的应力值。图6－10 所示为在裂纹产生前时刻竖直直径上各点应力理论值解与数值解对比，数值模拟结果与经验公式得到的结果吻合较好，说明扩展有限元模拟巴西实验是可靠的。在加载直径方向拉应力最大达到抗拉强度6 MPa，由于标准巴西实验中圆盘上下两端压应力集中严重，最大压应力达到105.5 MPa。
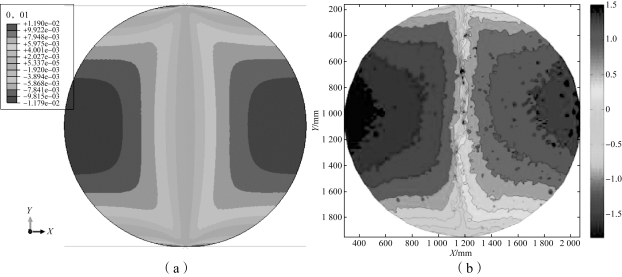
图6－9 圆盘试样开裂前位移场分布（见彩插）
（a）计算中水平位移场；（b）实验中水平位移场［9］
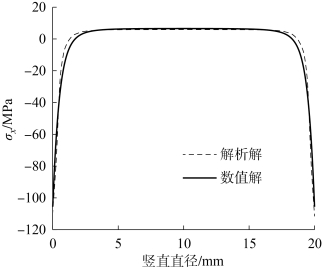
图6－10 竖直直径上各点σx值的数值解和解析解
图6－11 所示为PBX 标准巴西实验的载荷随位移变化曲线，载荷起初随着加载位移增大呈线性增大。当加载位移为0.199 7 mm 时达到最大载荷211 N，此时圆盘中心点的拉伸应力达到抗拉强度裂纹产生［图6－12 （a）］。随着裂纹的扩展，载荷降低，当降低到局部最小载荷152.9 N 时，形成贯通裂纹［图6－12 （c）］。然后由于圆盘受压，载荷再缓慢上升，这与文献［7］中的实验曲线比较一致。图6－12 所示为裂纹起裂到完全贯穿圆盘的过程，由图可以看出，标准巴西实验中，裂纹首先从圆盘中心处产生，然后沿加载直径方向扩展，最终形成贯通整个试件的宏观裂纹，圆盘发生劈裂破坏变为两半，计算结果和实验结果［图6－12 （d）］比较一致。
图6－11 数值模拟得到的加载载荷位移曲线
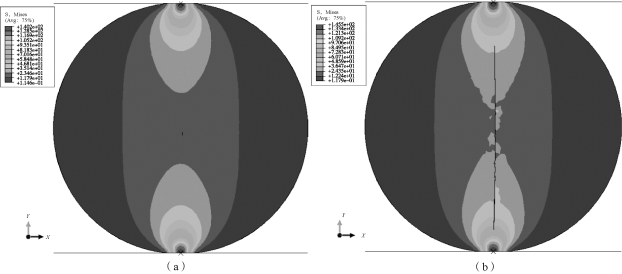
图6－12 圆盘试样破坏过程
（a）起裂（u＝0.199 7 mm）；（b）裂纹扩展（u＝0.200 5 mm）
图6－12 圆盘试样破坏过程（续）
（c）裂纹贯穿试样（u＝0.201 7 mm）；（d）实验中裂纹贯穿试样［6］
对标准巴西实验、圆弧巴西实验和橡胶垫巴西实验三种加载方式下圆盘上的应力分布和破坏过程进行了计算比较。图6－13 所示为三种加载方式下圆盘开裂时刻的von Mises 应力场分布，结果表明，应力沿圆盘中心轴均匀对称分布，在圆盘上、下接触位置均出现压应力集中区域。图6－14所示为圆盘开裂前加载直径上σx和σy的分布。三种不同加载方式导致应力分布的差异较大，σx值在离加载头较近时受到压缩作用为负值，标准巴西实验压缩应力最大，其次为圆弧巴西实验和衬垫巴西实验，在中心点附近受拉伸作用为正值，拉应力最大值均为6 MPa。在三种加载方式下中心点附近σy值差异不大，而在上、下两端有明显不同，其中标准巴西实验中最大应力值为155 MPa，而圆弧巴西实验和衬垫巴西实验中最大应力值分别为106 MPa 和62 MPa。计算结果表明，改变加载形式对应力集中有着明显的改善。
图6－13 三种巴西实验开裂前最大主应力场分布
（a）标准巴西实验；（b）圆弧巴西实验；（c）衬垫巴西实验
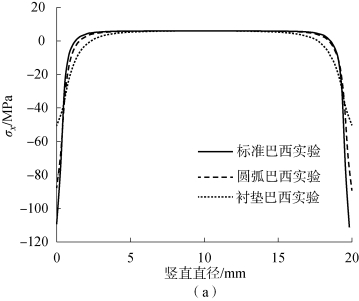
图6－14 三种巴西实验中y 轴上σx和σy应力分布
（a）y 轴上σx值分布
图6－14 三种巴西实验中y 轴上σx和σy应力分布（续）
（b）y 轴上σy值分布
图6－15 所示为三种加载方式下圆盘试样最终破坏形式和对应的von Mises 应力场分布图，在标准巴西实验试样中最大von Mises 出现在试样与加载装置接触的部位，圆弧巴西实验最大值所在位置与标准巴西实验类似，橡胶垫巴西实验由于衬垫的变形缓解应力集中，最大应力范围较广泛。三种实验中裂纹扩展均在中心处起裂，快速向两端扩展，最终试样劈裂为两半。通过比较可以发现，橡胶垫巴西实验可以有效降低接触应力，同时保证破坏形态基本一致，可以更精确地测量被测试样的间接拉伸强度。
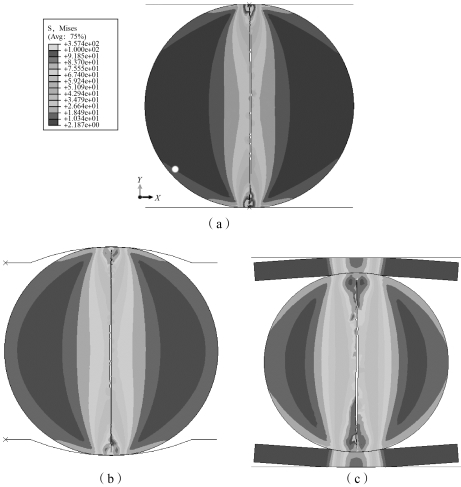
图6－15 三种巴西实验圆盘破坏时的von Mises 应力场分布
（a）标准巴西实验；（b）圆弧巴西实验；（d）衬垫巴西实验
有关高聚物黏结炸药损伤断裂的数值模拟的文章
- 详细阅读
-
优化后：计算结果与分析详细阅读
比较CB3和CB1的计算结果，将静导电杆的形状从水平U型改为平板型，电动斥力有所减小，说明水平U型通过改变电流的方向，有利于加强触头区域的磁场及相应的电动斥力，这一点也和图6-20的结果相一致。对CB1和CB2来说，FH分别为40.33N和38.45N，同表6-4的结果相比，有一定的差别，这主要是由于导电回路产生的磁场对动触头上电动斥力的影响引起的。表6-4 5个模型在10kA电流时的电动斥力计算结果......
2023-06-15
-
干细胞美容：效果与安全性分析详细阅读
所谓干细胞美容，就是把干细胞注射到皱纹部位的真皮浅层，让干细胞在皮肤中增殖，分化成皮肤细胞，把衰老受损皮肤的皱纹“撑”平，让皮肤恢复光滑和弹性。然而，这并不意味着干细胞美容完全安全。一方面，干细胞的增殖和分化都不容易控制，如果注射的干细胞增殖过多，就有可能不但填平了皱纹，还把那个部位的皮肤撑了出来，“矫枉过正”对于爱美人士恐怕是另一种残酷的折磨。另一方面，干细胞自身具有致瘤性的可能。......
2023-10-28
-
6.4.4 迁移学习模型的测试结果与分析详细阅读
针对本章构建的迁移学习模型，根据上述实验设置的超参数值和最佳冻结层数，分别在KTH-TIPS和UMD纹理库上开展实验，对本章构建的迁移学习模型进行最终的测试，以便获得在测试集上的纹理识别精度。对UMD纹理库进行划分，其中每类的20个样本作为训练集，10个样本作为验证集，10个样本作为测试集。......
2023-06-29
-
展成磨削法的方法的分析介绍详细阅读
常见有以下几种磨削方法。采用15°/ 20°磨削法磨削齿轮，齿面上是网状纹，它对齿面润滑有利；采用0°磨削法可对被磨齿轮的齿形进行修正及磨削鼓形齿。图16-2 双片蝶形砂轮磨齿方法a)15°/20°磨削法 b)0°磨削法2)采用钢带基圆盘展成和分度盘分度，磨削齿轮精度高。2)磨头往复运动有冲击，影响加工质量，磨削齿轮精度较前一种磨削方法低。2)展成运动和分度运动是连续的，因此生产率很高。......
2023-06-28
-
计算结果与分析的综合报告详细阅读
为了验证黏结剂Estane 参数的有效性，首先对黏结剂在应变率分别为0.005 s－1、0.5 s－1和15 s－1的条件下进行了模拟计算，得到黏结剂在不同应变率下的应力－应变曲线，并将计算结果与实验结果［16］进行对比。图7－14黏结剂Estane 数值计算和实验结果比较为了观察黏结剂的黏弹性作用对PBX9501 力学性能的影响，分别模拟了在应变速率为0.001 1 s－1、0.011 s－1、0.11 s－1和0.44 s－1条件下的单轴压缩实验，与实验测量值进行比较。......
2023-06-27
-
人工智能舞蹈交互系统实验结果与分析详细阅读
轨迹上的实心标记分别代表动作的起点和动作的终点。L1距离的定义如下：L2距离的定义如下：L3距离的定义如下：第二个实验方案的执行过程完全一样，只不过训练生成动作单元模板的动作集在动作库中的比例变为40%，而剩下的60%用来测试识别能力。基于不同的动作模板的实验结果见表2-4至表2-7。表2-10 第三组实验的识别率统计在第四组实验中，我们加入了动作集合2，这样一共有30种动作。......
2023-10-29
-
耐碱蚀性能的试验结果与铸铁材质关系分析详细阅读
如果碱液浓度超过80%，则普通的铁碳合金将受到严重的腐蚀。试验结果表明：耐电化学腐蚀性能高低的排序为：5-2、1-2、3-2、1-1，即镍铬合金灰铸铁的耐电化学腐蚀性最好，其次是稀土灰铸铁和锡铜合金灰铸铁，普通灰铸铁最差。......
2023-07-02
相关推荐