【主要内容】计算函数的导数的基础是求导基本公式和四则运算法则.求导基本公式：（1）C′=0（C是常数），（2）（xμ）′=μxμ-1，（3）（ax）′=axlna（常数a>0但a≠1），特别地，（ex）′=ex，（4），特别地，，（5）（sinx）′=cosx， （6）（cosx）′=-sinx，（7）（tanx）′=sec2x， （8）（cotx）′=-csc2x，（9）（secx）′=secx......
2023-10-27
拓展你的函数：增强形函数探究
【摘要】：传统有限元方法以连续函数作为形函数，导致在分析裂纹扩展等问题上无法使用，XFEM 在传统有限元位移模式中加入特殊的函数作为形函数，以反映不连续面的存在，这些特殊的函数被称作增强形函数。在XFEM 中，将对节点集Sh和Sc分别采用不同的增强形函数。这类形函数称为裂尖增强形函数。使用这两种增强形函数，含裂纹二维平板的位移场可以表示为式中：N为常规有限元的形函数，aJ和bK为节点附加自由度。
裂纹问题和夹杂问题分别代表两类间断，即强间断和弱间断。强间断问题存在位移的不连续而弱间断只存在应变不连续。传统有限元方法以连续函数作为形函数，导致在分析裂纹扩展等问题上无法使用，XFEM 在传统有限元位移模式中加入特殊的函数作为形函数，以反映不连续面的存在，这些特殊的函数被称作增强形函数。图6－2 所示含二维裂纹平板有限元模型，其中有一条半裂纹
穿过有限元网格终止于一单元内部。将有限元网格的所有节点记为集合S，把被裂纹完全切断的单元记作集合Sh（图中方框节点），把围绕裂尖的单元的节点记为Sc（图中圆圈节点）。在XFEM 中，将对节点集Sh和Sc分别采用不同的增强形函数。
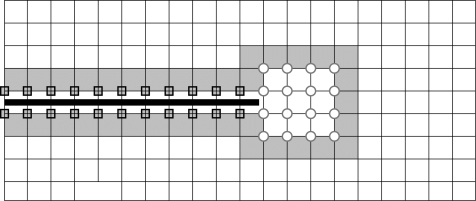
图6－2 二维裂纹中节点增强方案
（1）对于被裂纹完全穿过的单元，裂纹面两侧的位移场发生跳跃，增强形函数ψJ（x）可以采用如下形式：
式中：NJ（x）为通用增强形函数；H（x）是阶跃函数，可表示为
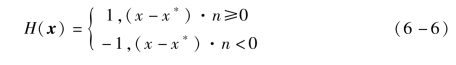
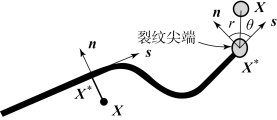
图6－3 光滑裂纹的切向和法向坐标
f（x）是水平集函数，可表示为
式中：n＋为间断线
上的单位法矢量。
对于不在
上的任意点x，f（x）是从点x 到
的最短距离，并且对此距离的正负定义为：如果点x 所在的位置与n＋指向一致则为正，否则为负。这类形函数被称为阶跃增强形函数（Heaviside Enrichment Function）。
（2）对于裂尖周围的节点，即集合Sc，ψJ（x）可以采用以下形式：
式中：Φ（x）为以下基函数用的线性组合：
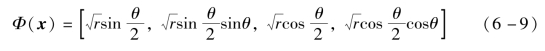
式中：r 和θ 为在裂尖极坐标系中定义的位置参数。
由于式（6－9）中的基函数是线弹性断裂力学中平面复合型裂纹裂尖位移场解析解的各项，用它们来构造裂尖形函数不仅可以表现裂纹面不连续的性质，同时还能精确捕捉裂尖位移场。这类形函数称为裂尖增强形函数（Tip Enrichment Function）。
使用这两种增强形函数，含裂纹二维平板的位移场可以表示为
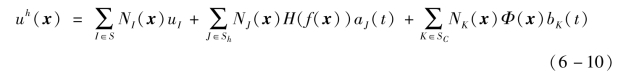
式中：N（x）为常规有限元的形函数，aJ和bK为节点附加自由度。
有关高聚物黏结炸药损伤断裂的数值模拟的文章
- 详细阅读
-
复变函数函数性态-复变函数及其应用详细阅读
如果是极点,指出它的级.解 令ζ = 则由于g(ζ)在ζ = 0解析且g 0,所以ζ = 0是的简单极点,因此z = ∞是f 的简单极点.......
2023-10-30
-
流线函数和速度势函数的可迭加性详细阅读
试述调和函数的定义、特性及应用。调和函数的意义。调和函数的特性。工程数学或高等数学发现，如果一个函数u(x,y)为调和函数，则该函数具备“可迭加”的特性。证明如果流体为x-y平面理想流体，流体在流动时的流线函数φ为调和函数，则函数具有迭加性。......
2023-06-29
-
复变函数与调和函数的关系详细阅读
前面我们证明了在区域D内的解析函数,其导数仍为D内的解析函数,下面我们用这个结论来研究解析函数与调和函数的关系.定义1 若φ(x,y)在平面区域D内有二阶连续偏导数,并且满足拉普拉斯(Laplace)方程则称φ=φ(x,y)在D内为调和函数.引入记号称为Laplace算子,则式(3.5.1)可简记为△φ=0.定理1 若函数f(z)=u(x,y)+iv(x,y)在区域D内解析,则u=u(x,y)和v......
2023-10-30
-
解析函数概念|复变函数及应用详细阅读
解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下：定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2023-10-30
-
复变函数与应用-复变函数及其应用详细阅读
幂函数w =zn(n ≥2为自然数)在z平面上处处可导,且除去原点外导数不为零,因此,在z平面上除去原点外是处处保角的.下面讨论w = zn在原点的性质.若令z = reiθ,w = ρeiφ,则由ρeiφ =rnelnθ,得由此可知,在w = zn映射下,z平面上的圆周|z| = r映射成w 平面上的圆周|w|=rn,射线arg z =θ0 映射成射线arg w =φ=nθ0,正实轴θ =0映射......
2023-10-30
-
函数的单调性及其应用详细阅读
【主要内容】设f′（x）>0（x∈（a，b））或f′（x）≥0（x∈（a，b），但仅在有限个点处取等号），则函数f（x）在（a，b）内单调增加；设f′（x）<0（x∈（a，b））或f′（x）≤0（x∈（a，b），但仅在有限个点处取等号），则函数f（x）在（a，b）内单调减少.注 （ⅰ）以上结论在a=-∞或b=+∞时仍成立；（ⅱ）当f（x）在[a，b]上连续时，端点x=a，x=b可以并入到f（x）的......
2023-10-27
-
幂函数的规定及性质-复变函数及其应用详细阅读
定义3 设α是任意一个复数,定义幂函数为w =zα =eαLnz(z 0).在α为正实数时,对z =0的情况进行规定：zα =0.幂函数是指数函数与对数函数的复合函数,根据对数函数的定义,有w =zα =eαLnz =eα(ln z+2kπi) =eα ln z·e2αkπi,(k为整数)由于Lnz = ln z+2kπi是多值的,所以w = zα也是多值的,且所取的不同数值的个数等于e2αkπi......
2023-10-30
相关推荐