水平集方法在图像处理中的应用

2025-09-29 理论教育版权反馈

【摘要】：由于XFEM 允许不连续面穿过单元，即网格独立于间断面，因此需要对不连续面进行几何描述，常用方法为水平集方法。水平集方法是一种用来追踪间断运动的数值方法。图6－1水平集函数f 和g 表示的二维裂纹在水平集方法中，与空间、时间有关的零水平集函数f用来描述与网格无关的间断。

由于XFEM 允许不连续面（如裂纹等）穿过单元，即网格独立于间断面，因此需要对不连续面进行几何描述，常用方法为水平集方法（Level Sets Method）。另外，在XFEM 构造增强形函数时往往也需要借助水平集函数。

水平集方法是一种用来追踪间断运动的数值方法。Stolarska 等［5］指出这种方法在XFEM 中不是必需的，并具有相当显著的优点：①间断的几何特性可以由水平集函数完全描述；②能在固定网格上计算间断的运动；③易于推广到多维的情况。

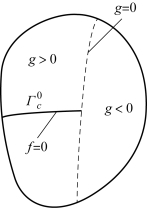
pagenumber_ebook=136,pagenumber_book=116

图6－1　水平集函数f 和g 表示的二维裂纹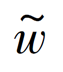 pagenumber_ebook=136,pagenumber_book=116

在水平集方法中，与空间、时间有关的零水平集函数f（x（t），t）用来描述与网格无关的间断。因为增加了时间变量，所以水平集函数要比间断的维数增加一维。在计算过程中，间断上的点始终满足：

空间中满足这一条件的点形成一个集合γ（t）。在间断两边，水平集函数符号相反。在图6－1 中裂纹面的位置可以通过零水平集函数f（x（t），t）描述。(https://www.chuimin.cn)

一种常用的水平集函数构造方法是符号距离函数［5］，即

式（6－2）的物理意义是在计算域内任意一点的距离符号函数等于这一点到间断的最短距离，并且间断两边的点具有不同的符号。因此，它具备水平集函数的基本特性：在间断上等于0，在间断两侧异号。对于有端点的间断，如图6－1 所示，裂纹面终止于求解域内部，仅仅一个水平集函数f 是不够的，因为它无法反映出裂纹尖端的位置，为此对于每一个端点还分别定义一个新的水平集函数g。假设知道了端点xi的移动速度vi，则与此端点对应的水平集函数gi可以定义为

从式（6－3）可以看出，gi＝0 代表了经过端点xi，并与裂纹扩展速度vi垂直的一条线，即该直线相交于裂纹尖端并垂直于裂纹扩展方向，它刻画了裂尖的位置。在这条直线的两边，gi符号相反（水平集函数基本特性）。

使用该方法，图6－1 中裂纹面的位置可以通过水平集函数表示为

水平集方法在图像处理中的应用

相关推荐