首页理论教育有限元模型设计与应用

有限元模型设计与应用

2023-06-27 理论教育版权反馈

【摘要】：图5－12 所示为有限元模型，由弹体、PBX 装药、混凝土靶板组成，单元类型为三维实体单元SOLID164，利用六面体单元划分映射网格，靶板中心区域网格加密。软化曲线选择线性软化，该模型通过无量纲裂纹宽度ω 表征装药损伤情况，单元裂纹宽度l 与ω 的关系为表5－7PBX 装药的材料参数

基于内聚裂纹模型编写了LS－DYNA 的子程序，对装填PBX 装药的弹体侵彻半无限厚混凝土靶板进行数值模拟。图5－12 所示为有限元模型，由弹体、PBX 装药、混凝土靶板组成，单元类型为三维实体单元SOLID164，利用六面体单元划分映射网格，靶板中心区域网格加密。为了提高计算效率，考虑到模型的对称性，建立1／4 模型，对称面施加对称约束，共划分约20 万个单元。混凝土靶板侧面和底部添加非反射界面。PBX 装药与弹体的接触类型为*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE，弹体与混凝土靶板的接触类型为*CONTACT_ERODING_SURFACE_TO_SURFACE。弹体直径为60 mm，弹头曲径比为2.6，弹体长径比为4.42，装药长度为180.5 mm，壳体厚度为5 mm，混凝土靶板为φ600 mm ×800 mm 的圆柱形。弹体正侵彻混凝土靶板，弹体侵彻速度为600 m／s。

pagenumber_ebook=107,pagenumber_book=87

图5－12　整体装药形式下弹体侵彻混凝土模型

弹体采用双线性弹塑性本构，考虑各向同性塑性硬化，应变率效应的影响采用Cowper－Symonds 材料模型描述，其关系式为

pagenumber_ebook=107,pagenumber_book=87

式中：σ 为屈服应力；ε·为应变率；为等效塑性应变；σ0为材料的静态屈服应力；C、p 为Cowper－Symonds 应变率参数；Ep为材料的塑性硬化模量；β 为硬化参数。

弹体的材料参数如表5－5 所示。

表5－5　弹体的材料参数［7］

pagenumber_ebook=108,pagenumber_book=88

混凝土材料采用HJC 模型。该模型综合考虑了混凝土材料在高应变率大变形下响应，其涉及的参数可分为基本强度参数、损伤参数、极限面参数和状态方程参数等四类。其等效屈服强度是压力、应变率及损伤的函数，包含材料损伤的影响，用归一化等效应力描述［8］，即

式中：σ*＝σ／fc为归一化等效应力，σ 为等效应力，fc为准静态单轴抗压强度；D（0≤D≤1.0）为损伤因子，损伤积累是塑性体积应变、等效塑性应变及应力的函数；P*为归一化压力；ε*为量纲为1 的应变率；A 为归一化内聚强度；B 为归一化压力硬化系数；C 为应变率系数；N 为压力硬化指数。

混凝土靶板的材料参数如表5－6 所示。

表5－6　混凝土靶板的材料参数

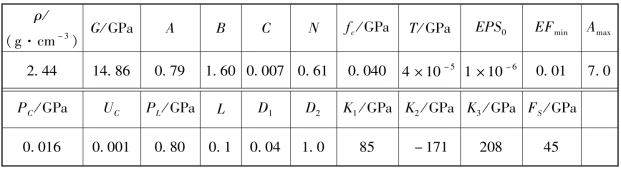
pagenumber_ebook=108,pagenumber_book=88

PBX 装药采用基于内聚裂纹的自定义材料模型，K 和G 分别为材料的体积模量和剪切模量，ft为材料的拉伸强度，Gf为材料的断裂能，PBX 装药的材料参数如表5－7 所示。软化曲线选择线性软化，该模型通过无量纲裂纹宽度ω 表征装药损伤情况，单元裂纹宽度l 与ω 的关系为

pagenumber_ebook=108,pagenumber_book=88

表5－7　PBX 装药的材料参数

pagenumber_ebook=108,pagenumber_book=88