威布尔随机分布解析

2023-06-27 理论教育版权反馈

【摘要】：为了考虑PBX 参数的非均匀性，引入威布尔概率分布，实现各单元材料属性随机力学参数赋值。为了清晰地描述PBX 材料破坏损伤过程，对弹性模量、泊松比、拉伸强度、断裂能等参数进行威布尔概率统计分析，在巴西圆盘实验的有限元计算中得到应用。图4－11威布尔随机数的分布函数图4－12巴西实验有限元模型

PBX 是一种具有复杂力学性质的非均匀准脆性材料。基于经典力学理论的力学模型忽略了PBX 内部细观结构的非均匀性，不足以表达PBX 整个变形过程所表现的复杂性。假设材料中分布着大量的微裂纹，材料在宏观上是统计均匀的，即其细观结构的统计规律（宏观性质）与位置无关。PBX 中炸药颗粒尺度为0.1 mm 甚至更小，对于尺度为10～20 mm 量级的试样，细观结构分布的不均匀对宏观性质的影响不能忽略。而如果试样尺度达到100 mm 量级，细观非均匀分布的影响则可以忽略。为了考虑PBX 参数的非均匀性，引入威布尔概率分布（Weibull distribution），实现各单元材料属性随机力学参数赋值。

1937年，Waloddi Weibull 率先提出用概率的方法描述材料的非均匀性。他认为精确测量破坏时的强度是不可能的，但是给定应力水平下发生破坏的概率是可以定义的，基于这一思想，推导了基于一维杆条件的破坏概率模型，认为最薄弱环节的破坏将导致整体破坏。随后，苏联学者沃尔科夫［16］提出了新的统计强度理论，认为只有非均匀材料中的破裂数量累积到一定程度后才能发生宏观破裂，而不是一点破裂整个试件就失效。

利用统计的方法对PBX 进行描述，是一种有效的描述材料非均质的方法。由于每个单元所包含的颗粒和黏结剂的物理力学性质差别和不同数量、不同几何形状微缺陷的存在，各单元的力学性质（弹性模量、强度、泊松比和断裂能等）是离散的。这里，假设组成材料细观单元的力学性质满足威布尔分布，该分布可以按照如下的概率密度函数定义，即

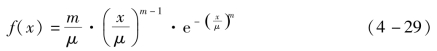
pagenumber_ebook=89,pagenumber_book=69

式中：x 为材料的力学参数（如弹性模量、泊松比、强度、断裂能等）；μ 为材料的力学性质的平均值；m 为分布参数，又称为均质度系数，定义了分布密度函数f（x）的形状，其物理意义反映材料的均质性。

均质度系数描述了材料内部力学性质的离散程度，当m 较大时，单元的力学特性集中在一个较窄的分布范围内，意味着材料内部力学特性较为均匀；而当分布参数的数值较低时，材料细观单元的力学性质分布范围很宽，此时则意味着材料力学性能的离散程度高。由此可见，m 参数反映了数值模拟模型中材料内部的均质性。

在脆性材料的损伤断裂过程中，随着m 的增加，材料的强度和峰值强度对应的应变量均有不同程度的提高［17］。均质度系数对材料的非线性行为有影响，当降低均质度时，材料的非线性行为明显增强，而且破裂后期行为表现出软化行为；反之，材料线性增强，变形后期表现出显著的脆性。因此，通过多次模拟统计发现，m 取15 时，符合PBX 材料的力学特性，如图4－11 所示，该图描述了弹性模量为10.2 GPa，5 000 个随机数统计的密度函数图。为了清晰地描述PBX 材料破坏损伤过程，对弹性模量、泊松比、拉伸强度、断裂能等参数进行威布尔概率统计分析，在巴西圆盘实验的有限元计算中得到应用。

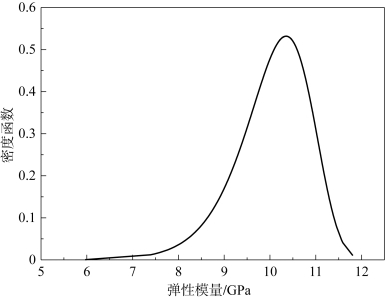
pagenumber_ebook=90,pagenumber_book=70

图4－11　威布尔随机数的分布函数

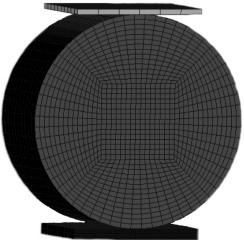
pagenumber_ebook=90,pagenumber_book=70

图4－12　巴西实验有限元模型

威布尔随机分布解析

相关推荐