图3.2.16 边倒圆特征2Step1.新建文件。②进入草图环境,绘制图3.2.2所示的截面草图。图3.2.19 定义移除面单击按钮,完成拔模特征的创建。在绘图区域中选取XY基准平面,在文本框中输入值35,其他参数采用系统默认设置值。图3.2.20 拉伸特征3Step6.创建图3.2.8所示的基准平面2。Step7.创建图3.2.9所示的草图1。Step10.创建图3.2.12所示的零件特征——网格曲面。选取图3.2.14b所示的修剪体特征为镜像特征。......
2023-06-22
在黏聚裂纹模型编译中,裂纹张开位移的求解是非常关键的,本程序采用牛顿-拉夫森方法实现。牛顿-拉夫森迭代法(Newton-Raphson's method)也称牛顿迭代法,它是数值分析中最重要的方法之一,不仅适用于方程或方程组的求解,还常用于微分方程和积分方程求解。
牛顿迭代法也称为牛顿切线法,这是由于f(x)的线性化近似函数l(x)=f(x0)+f′(x0)(x-x0)曲线y=f(x)过点(x0,f(x0))的切线而得名的,求f(x)的零点代之以求l(x)的零点,即切线l(x)与x 轴交点的横坐标,如图4-2 所示,这就是牛顿切线法的几何解释。
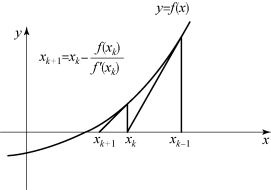
图4-2 牛顿迭代法
实际上,牛顿迭代法也可以从几何意义上推出。利用牛顿迭代公式,由xk得到xk+1,从几何图形上看,就是过点(xk,f(xk))作函数f(x)的切线lk,切线lk与x 轴的交点就是xk+1,则

整理后可以得出牛顿迭代公式:

牛顿迭代法实质上是一种线性化方法,其基本思想是将非线性方程逐步归结为某种线性方程来求解。为了求解这个问题,设R(w)是残值矢量,其范数|R(w)|作为一个判断阈值,每次迭代时都要进行判断,根据牛顿迭代法的收敛,以确定求解是否收敛,则式(3-84)可写为
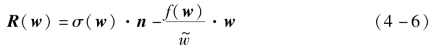
假设现有近似解为wn,通过方程求解得到更准确的近似解wn+1,每一步的迭代得到更精确的值,可得
![]()
其中

将式(4-8)分解为三个部分,即
![]()
式中:An(w)、Bn(w)、Cn(w)分别表示为

式中:I 为三阶单位张量。
在An(w)部分,根据有限元方法,将应力张量转化为在有限元分析软件中容易求解的应力矢量,即
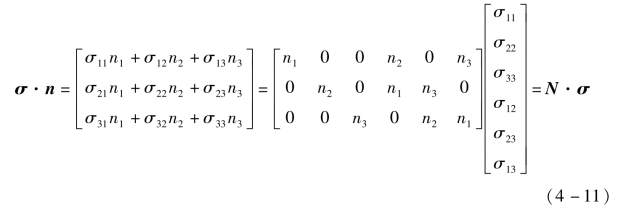
除此之外,可以得到

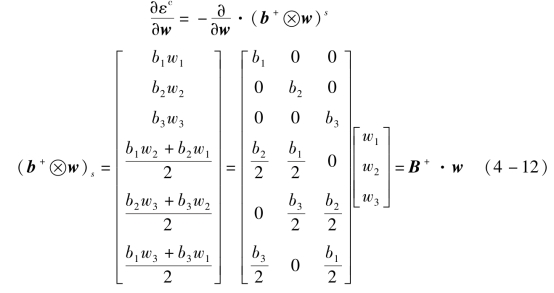
则
![]()
式中:Cept 的定义为![]() ,即材料弹性模量的四阶张量;矩阵N 由矢量n 得到,矩阵B+由矢量b+得到。
,即材料弹性模量的四阶张量;矩阵N 由矢量n 得到,矩阵B+由矢量b+得到。
对于Bn(w)部分,需考虑两种状态即加载与卸载。在加载中,等效裂纹宽度![]() 与裂纹宽度相等|w|并且持续变化。在卸载过程中,等效裂纹宽度
与裂纹宽度相等|w|并且持续变化。在卸载过程中,等效裂纹宽度![]() 保持不变。所以,可以求解
保持不变。所以,可以求解![]() 与w 的偏量比值,在加载条件下,有
与w 的偏量比值,在加载条件下,有
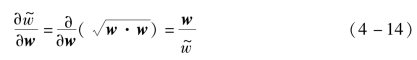
所以,在加载条件下,裂纹是持续张开的,有
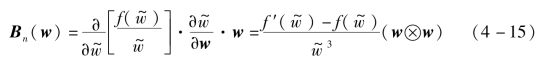
在卸载情况下,等效裂纹宽度保持不变,则导数为0,因此B 部分为0。假设连续体为线弹性本构模型,则根据弹性力学可知


图4-3 所示为牛顿迭代法的编译流程。首先初始化子程序中的变量,计算式(4-11)中的矩阵N 和式(4-13)中的B+;然后判断残值矢量的范数![]() 是否大于设定的阈值,如果大于阈值,则进入循环:根据单元的连续应变增量Δεc可以计算得到新的应力,记为σplus。同时,也可以计算出刚度矩阵Cept。根据前一步得到的
是否大于设定的阈值,如果大于阈值,则进入循环:根据单元的连续应变增量Δεc可以计算得到新的应力,记为σplus。同时,也可以计算出刚度矩阵Cept。根据前一步得到的![]() ,根据软化曲线可以得到
,根据软化曲线可以得到![]() 和
和![]() 。根据式(4-6)计算得到新的Rres,并最终得到D [式(4-8)],此时再判断是否小于阈值。这是加载过程中的计算步骤,这时需要判断
。根据式(4-6)计算得到新的Rres,并最终得到D [式(4-8)],此时再判断是否小于阈值。这是加载过程中的计算步骤,这时需要判断![]() 新计算得到的
新计算得到的![]() 与历史裂纹张开位移
与历史裂纹张开位移![]() 的大小。如果
的大小。如果![]() ,则单元是加载过程;若
,则单元是加载过程;若![]() ,则为卸载过程,需要重新计算裂纹张开位移。与加载过程不同的是,历史张开位移
,则为卸载过程,需要重新计算裂纹张开位移。与加载过程不同的是,历史张开位移![]() 在卸载过程中不会发生变化。
在卸载过程中不会发生变化。
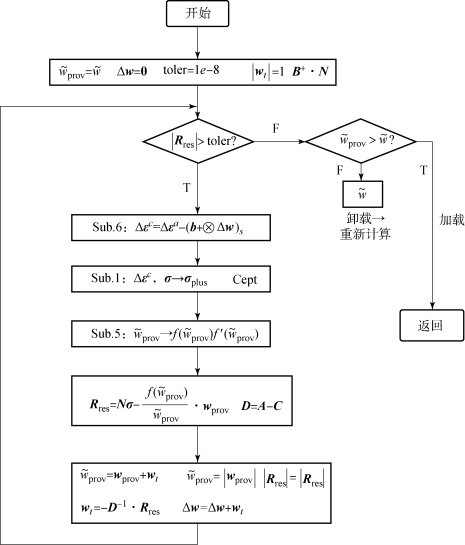
图4-3 牛顿迭代法编译流程
有关高聚物黏结炸药损伤断裂的数值模拟的文章

图3.2.16 边倒圆特征2Step1.新建文件。②进入草图环境,绘制图3.2.2所示的截面草图。图3.2.19 定义移除面单击按钮,完成拔模特征的创建。在绘图区域中选取XY基准平面,在文本框中输入值35,其他参数采用系统默认设置值。图3.2.20 拉伸特征3Step6.创建图3.2.8所示的基准平面2。Step7.创建图3.2.9所示的草图1。Step10.创建图3.2.12所示的零件特征——网格曲面。选取图3.2.14b所示的修剪体特征为镜像特征。......
2023-06-22

图6.6.11 创建拉伸曲面2图6.6.12 截面草图Step3.将拉伸曲面1和拉伸曲面2进行合并。图6.6.13 合并曲面Step4.将封闭曲面面组变成实体特征。在“智能选取”栏中选取选项,然后选取图6.6.24所示的曲面;选择下拉菜单命令,系统弹出操控板,在操控板中按下“去除材料”按钮,方向箭头如图6.6.24所示。选择下拉菜单命令;选取图6.6.25所示的模型......
2023-06-20

玩具飞机的零件模型树如图19.2.1所示。选取XY基准平面为草图平面;进入草图环境,绘制图19.2.4所示的样条曲线,使样条曲线定义点1位置与构造线1水平相切,样条曲线定义点2位置与构造线2水平相切。选取ZX基准平面为草图平面,绘制图19.2.6所示的曲线。图19.2.4 草图2说明:现在绘制的是骨架轮廓的一半,通过镜像操作完成另一半的绘制。Step6.创建图19.2.8所示的基准平面2。......
2023-06-22

选择下拉菜单命令,系统弹出“基准平面”对话框;在区域的下拉列表中选择选项,在区域单击按钮,在绘图区选取XY基准平面为参考平面,在文本框中输入值40,调整偏置方向如图13.2.3所示;其他参数采用系统默认设置值;单击按钮,完成基准平面1的创建。Step3.创建图13.2.3所示的基准平面1。选择下拉菜单命令;选取基准平面2为草图平面;进入草图环境,绘制图13.2.8所示的草图2;单击按钮,退出草图环境。Step8.创建图13.2.11所示的直线特征2。......
2023-06-22

选择下拉菜单命令,系统弹出“创建草图”对话框;选取XY基准平面为草图平面,单击按钮;进入草图环境,绘制图10.2.1所示的草图1;选择下拉菜单命令,退出草图环境。Step6.创建图10.2.8所示的拉伸特征1。Step7.创建图10.2.9所示的基准平面。......
2023-06-22

Step4.创建图11.2.5所示的基准平面1。图11.2.6 定义参照点说明:完成基准平面1的创建后,不用退出“基准平面”对话框,以便创建其他基准平面。图11.2.7 基准平面2图11.2.7 基准平面2图11.2.8 定义参照线图11.2.8 定义参照线Step6.创建图11.2.9所示的基准平面3。选择下拉菜单命令,系统弹出“创建草图”对话框;选取基准平面1为草图平面,选取XY平面为参考,取消选中区域的复选框;单击按钮,进入草图环境,绘制图11.2.11所示的草图2;单击按钮,退出草图环境。......
2023-06-22

Step1.新建模型文件。图20.3.2 草图2说明:在添加样条曲线上点的对称约束时,需要在“启用捕捉点”工具条中将“控制点”选项打开。通过单击区域的按钮调整偏置方向,如图20.3.4所示;其他参数采用系统默认设置值;单击按钮,完成基准平面1的创建。Step7.添如图20.3.6所示的基准平面2。选择下拉菜单命令,系统弹出“创建草图”对话框;选取基准平面2为草图平面,绘制图20.3.8所示的草图5。Step9.添加图20.3.9所示的基准平面3。......
2023-06-22

Step5.创建图1.2.4所示的基准平面1。选择下拉菜单命令,在绘图区选取图1.2.6所示的草图2为扫掠的截面曲线串,选取图1.2.4所示的艺术样条特征和图1.2.5所示的草图1为扫掠的引导线串,并分别单击中键确认。选择下拉菜单命令,在区域中单击按钮,选取图1.2.8所示的曲面为加厚的对象。图1.2.7 扫掠特征图1.2.8 加厚特征Step10.保存零件模型。......
2023-06-22
相关推荐