图2-1 现金流量图现金流量图包括三大要素：大小、流向、时间点。各时间点上的垂直线段箭头向上表示现金流入，箭头向下表示现金流出；即有资金流入时，此时现金流量为正值；资金流出时，现金流量为负值。静态即不考虑资金时间价值，动态则需折现计算。2）评价原则：费用最小的方案最优。......
2023-09-25
无网格移动最小二乘近似法及其应用
【摘要】：Belytschko 等［12］提出基于移动最小二乘近似和Galerkin离散方案的无网格迦辽金法，具有较好的协调性和稳定性，精度和收敛速度高于有限元法，目前已被广泛应用于裂纹扩展、成型加工、渗流问题等不同工程领域。在LS－DYNA 软件中，借助可视判据和快速变换算法［14］，在EFG 法中引入了内聚力模型来模拟裂纹扩展［15］。在LS－DYNA 软件中，EFG 法采用的内聚力模型是初始刚性的线性内聚力模型。
无网格法的提出是为了解决有限元方法在大变形、裂纹扩展等不连续问题面临的困难。在计算时，无网格法不用生成网格，只需要按照一系列任意分布的坐标点构造插值函数离散控制方程就可以了，从而保证了计算的精度。目前已提出10 余种无网格法［9］，不同算法的主要区别在于所使用的试探函数和微分方程的等效形式不同。较有代表性的有以Lagrange 方法为基础的光滑粒子流体动力学（Smooth Particle Hydrodynamics，SPH）法、以Euler 方法为基础的无网格迦辽金（Element Free Galerkin，EFG）法。在解决爆炸冲击问题时，SPH 法存在拉应力不稳定、边界处理模糊等问题，对于断裂扩展问题的模拟不够理想［10，11］。Belytschko 等［12］提出基于移动最小二乘近似和Galerkin离散方案的无网格迦辽金（Element Free Galerkin，EFG）法，具有较好的协调性和稳定性，精度和收敛速度高于有限元法，目前已被广泛应用于裂纹扩展、成型加工、渗流问题等不同工程领域。EFG 法的基本思想是：求解域Ω内的函数u（x），可根据该域内的若干已知离散点，由移动最小二乘法构造其近似函数uh（x），即
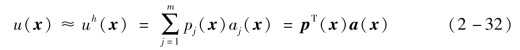
式中：pj（x）为基函数；m 为基函数的项数；a（x）为与x 相关的系数。
由二次方程式J（x）求极小值，可得
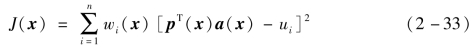
式中：wi（x）为各节点对应的权函数，权函数只在节点i 周围一个有限区域内大于0，该区域Ωi称为权函数的影响域，如图2－4 所示。近似函数uh（xi）是待求函数u（xi）在计算点i 邻域Ωi内的加权最小二乘意义下的局部最佳近似。各个点的局部近似函数uh（xi）在点i 的集合就构成了待求函数在求解域Ω 内的全局近似函数。
Klein 等［13］最先在无网格法中引入了内聚断裂分析的技术，利用内聚力模型来描述断裂发展的过程。为模拟裂纹扩展，除了裂纹扩展判据外，还需要在近似函数中引入不连续性，一般多采用较简单的可视判据扩充近似函数［9］，如图2－5 所示。在LS－DYNA 软件中，借助可视判据和快速变换算法［14］，在EFG 法中引入了内聚力模型来模拟裂纹扩展［15］。在初始构型中，由内聚力面将区域分为Ω＋0和Ω－0两部分，达到临界位移后，内聚面两侧的应力为0，内聚力面即转变为裂纹面。在LS－DYNA 软件中，EFG 法采用的内聚力模型是初始刚性的线性内聚力模型。模拟断裂问题时，不需要在材料或结构中预置裂纹，对于三维模型只要建立四面体背景网格。合理选取模型的参数后，就能够模拟材料或结构开裂过程中的宏观力学响应。目前，LS－DYNA 软件中EFG 法的断裂模拟功能还不够完善，与有限元法相比，计算量较大，模拟结构的动态断裂问题时，需借助背景网格进行数值积分，裂纹路径预测不够准确，单元侵蚀算法容易使计算过程不稳定，相信以后会得到改进。
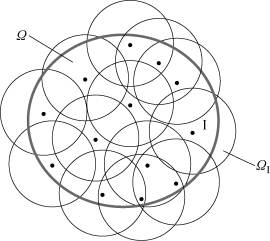
图2－4 节点的圆形影响域
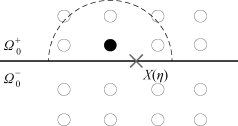
图2－5 可视判据图示
有关高聚物黏结炸药损伤断裂的数值模拟的文章
- 详细阅读
-
最小二乘基窗设计算法优化详细阅读
图3-31 基于最小二乘的基窗F卷积窗C及滤波器特性实现上述结果的MATLAB代码如下：图3-31 基于最小二乘的基窗F卷积窗C及滤波器特性实现上述结果的MATLAB代码如下：卷积窗C性能参数B=0.2165，A=-14dB，D=-10.15dB。对比图3-16七种基窗可看出，利用最小二乘得到的基窗综合性能最好。此外，基于此结果基窗F的滤波器具有最小的均方误差。......
2023-06-23
-
移动平滑法优化方案详细阅读
移动平滑法就是对所取得的统计数据逐点推移，分段平均，以期最后得到一组具有较明显趋势的新数据。移动平滑法的预测程序框图见图9.2。图9.2移动平滑法的预测程序框图 某灌区历年人均林果产值见表9.3，试用移动平滑法建立预测模型，并求1999—2005年该灌区人均林果产值的预测值。图9.3人均林果产值的自然曲线及移动平滑预测曲线图由图9.3可知，对于直接用一次或二次移动平滑模型预测会出现滞后现象。......
2023-06-30
-
流体网格法及其在解决激波问题中的应用详细阅读
因此在用流体网格法求解流体动力学方程时，必须考虑对激波的处理，即解决间断的问题。本节在介绍流体网格法以及说明流体网格法差分过程中均提到了差分中的人工粘性系数q，这种加入人工粘性系数的方法目前在跨音速流动的数值计算中是非常有效的。......
2023-07-02
-
大学物理实验：最小二乘法的线性回归详细阅读
在一元线性回归中，确定常数A和B，相当于在作图法中求直线的截距和斜率。图0-4密集分布 图0-5分散分布 方程的线性回归，用手工计算是很麻烦的。但是，不少袖珍型函数计算器上均有线性回归的计算键，计算起来极为方便，因此，线性回归的应用日益普及。......
2023-11-02
-
平滑预测法：指数平滑预测法和移动平均预测法详细阅读
平滑预测法就是根据过去演变特征预测对象自身时间过程演变规律及未来趋势。平滑预测法包括了移动平均预测法和指数平滑法。加权指数平滑预测法需进行三次移动。一次指数平滑预测法也是一种加权预测法，加权系数为α。......
2023-07-15
-
网格划分方法与应用实例详细阅读
单击Mesh模块图标，进入网格划分模块，相应的工具条中显示出网格处理的快捷命令图标。设置Average Mesh Size为10，单位为mm。单击Apply按钮，生成一维梁单元，总计69个梁单元。单击Save按钮，保存文件。......
2023-10-27
-
齿轮双频感应淬火技术（SDF法）及其应用详细阅读
美国ELECTROHEAT公司和德国ELDEC公司等提出的同时双频感应淬火，才真正使齿轮的轮廓淬火获得成功。图7-9 现代化齿轮同时双频感应淬火示意图图7-10 齿轮同时双频感应加热及其硬化层分布1—齿轮 2—感应圈SDF法优点与用途1）优点。同时双频感应加热，易于集成在现有机加工生产线上。很显然，SDF同步双频感应淬火具有更小的畸变量和更均一的轮廓硬化层图7-11 行星齿轮简图图7-12 行星齿轮感应淬火畸变量对比a）SDF同时双频感应淬火 b）中频感应淬火2）应用。......
2023-06-29
相关推荐