CAE软件通常可分为通用分析软件和行业专用软件。它从功能上可以划分为求解器软件和前后处理软件，从应用方向和领域上又可以分为主要面向结构领域的有限元分析软件和针对流体力学领域的计算流体力学分析软件，以及解决多物理场耦合问题的多场耦合分析软件。在管道行业中，CAEPIPE是最主要的分析软件。......
2023-10-27
ANSYS/LS-DYNA有限元软件介绍
【摘要】：ANSYS 软件是融结构、热、流体、电磁、声学于一体的大型通用有限元商用分析软件。后来，DYNA 更名为LS－DYNA，并经过多年的发展与改进，功能更加强大，应用范围不断扩大。1996年，LSTC 公司与ANSYS 公司合作推出ANSYS／LS－DYNA，大大增强了LS－DYNA 的分析能力，用户可以充分利用ANSYS 的前后处理器和统一数据库的优点［1～2］。它与材料模型有关，在LS－DYNA 程序中有金属和非金属材料模型近100
ANSYS 软件是融结构、热、流体、电磁、声学于一体的大型通用有限元商用分析软件。由世界上最大的有限元分析软件公司之一美国ANSYS 公司开发，它能与多数计算机辅助设计（CAD）软件接口，实现数据的共享和交换，是现代产品设计中的高级工具之一。
LS－DYNA 程序最初为DYNA 程序，它是由John O.Hallquist 博士于1976年在美国Lawrence Livermore National Laboratory （美国三大国防实验室之一）主持开发完成的。当时，主要用于求解三维非弹性结构在高速碰撞、爆炸冲击下的大变形动力响应，其目的主要是为北约组织的核武器弹头设计开发分析工具。后来，DYNA 更名为LS－DYNA，并经过多年的发展与改进，功能更加强大，应用范围不断扩大。1996年，LSTC 公司与ANSYS 公司合作推出ANSYS／LS－DYNA，大大增强了LS－DYNA 的分析能力，用户可以充分利用ANSYS 的前后处理器和统一数据库的优点［1～2］。
LS－DYNA 程序是功能齐全的非线性分析程序包，可以处理各类复杂的非线性问题，特别适合求解各种二维、三维非线性结构的高速碰撞、侵彻和爆炸冲击等非线性问题，同时也可以求解传热及流固耦合等问题。它以Lagrange算法为主，兼有Euler 和ALE 算法；以显示求解为主，兼有隐式求解功能；以结构分析为主，兼有热分析、流体结构耦合分析；以非线性动力分析为主，兼有静力分析功能。它具有丰富的单元库，有二维、三维实体单元，薄、厚壳单元，梁单元和弹簧、阻尼器单元，SPH 单元以及其他特殊用途的单元。它拥有超过150 种金属和非金属材料的本构模型。在接触分析方面，LS－DYNA 的全自动接触分析功能非常方便，有50 多种接触分析方式，可以求解柔性体与柔性体，柔性体与刚性体，刚性体与刚性体之间的接触问题。与它强大的计算功能匹配的还有功能齐全的前后处理软件，常用的前后处理软件有ANSYS、TRUEGRID、TAURUS、HYPEMESH、LSPREPOST 、FEMB等，这些软件方便了有限元建模和计算数据的处理。由于LS－DYNA 具有强大的数值模拟功能，在民用和国防领域有广泛的应用，如汽车、飞机的碰撞分析，金属成型，公路桥梁设计，电子产品的跌落分析，战斗部结构设计，侵彻过程和爆炸模拟分析，超高速碰撞模拟分析。
2.1.1.1 算法原理［3］
LS－DYNA 程序的主要算法采用Lagrangian 描述增量法。取初始时刻的质点坐标为Xi（i＝1，2，3）。在任意时刻t，该质点坐标为xi（i＝1，2，3）。这个质点的运动方程为
在t＝0 时，初始条件为
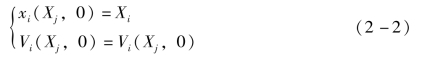
式中：Vi为初始速度。
动量方程可以表示为
式中：σij为柯西应力；fi为单位质量体积力；x¨i为加速度。
质量守恒方程为
式中：ρ 为当前质量密度；ρ0为初始质量密度。
能量方程用于状态方程计算和总的能量平衡，为
式中：V 为现时构形的体积；
为应变率张量；q 为体积黏性阻力；Sij＝σij＋（p ＋q）σij为偏应力；p 为静水压力，
。
LSDYNA 计算时要满足应力边界条件、位移边界条件和滑动接触面间断处的跳跃条件。其中，面力边界条件如图2－1 所示，可用下式计算，即
式中：nj（j＝1，2，3）为现时构形边界S1的外法线方向余弦；ti（i＝1，2，3）为面力载荷。
位移边界条件为
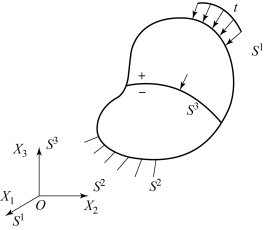
图2－1 边界示意图
式中：Ki（t）（i＝1，2，3）为给定位移函数。
滑动接触面间断处的跳跃条件为
伽辽金法弱形式平衡方程为
式中：δxi在S2边界上满足位移边界条件。
应用散度定理，有
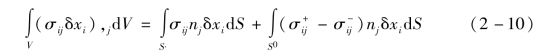
并注意到分部积分，有
式（2－9）可改写成虚功原理的变分列式：
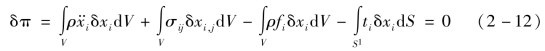
LSDYNA 中有限元的离散采用8 节点六面体实体单元（可退化为6 节点、4 节点实体单元），如图2－2 所示。这种单元运算速度快，精度也不错。
单元内任意点的坐标用节点坐标插值表示为
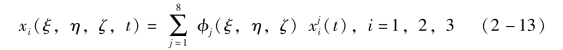
式中：ξ、η、ζ 为自然坐标；
为t 时刻第j 节点的坐标值；形状函数φj（ξ，η，ζ）可表示为
图2－2 8 节点固体单元
式中：（ξj，ηj，ζj）为单元第j 节点的自然坐标。
式（2－13）用矩阵表示为
式中：单元内任意点坐标矢量为
单元节点坐标矢量为
插值矩阵为
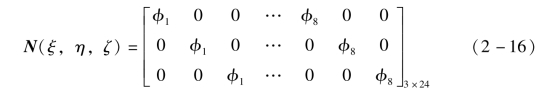
将式（2－15）代入式（2－12），得矩阵形式的表达式为
式中：n 为单元数；柯西应力矢量为
体力矢量为
面力矢量为
应变位移矩阵为
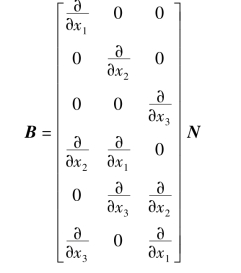
经单元计算并组集后，式（2－17）可以写为
或
式中：M 为总体质量矩阵；x¨（t）为总体节点加速度矢量；P 为总体载荷矢量，由节点载荷、面力、体力等形成；F 为单元应力场的等效节点力矢量（或称应力散度）组集而成，即
非线性动力分析程序用于工程计算，最大的困难是耗费机时过多，显式积分的每一时步，单元计算的机时占总机时的主要部分。采用单点高斯积分的单元计算可以极大地节省数据存储量和运算次数，但是单点积分可能引起零能模式，或称沙漏模态（Hourglassing mode），需加以控制。LS－DYNA 3D程序采用沙漏黏性阻尼控制零能模式，此时非线性运动方程组应改为
式中：H 为总体结构沙漏黏性阻尼力。
高速碰撞在结构内部产生应力波，形成压力、密度、质点加速度和能量的跳跃，给动力学微分方程组的求解带来困难。1950年，von Neumann 和Richtmyer 提出，将一个人工体积黏性q 加进压力项，使应力波的强间断模糊成在相当狭窄区域内急剧变化但却是连续变化的。
LS－DYNA 3D 程序的标准算法如下：
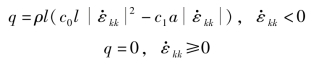
式中：特征长度
；a 为局部声速；ρ 为当前质量密度；应变率张量的迹
（默认值为1.5）和c1（默认值为0.06）为量纲为1 的常数。
引进人工体积黏性q 后，应力计算公式变成
式中：p 为压力；Sij为偏应力张量。
LS－DYNA 程序的运动方程考虑阻尼影响后，可得
其时间积分采用显式中心差分法，它的算法如下：
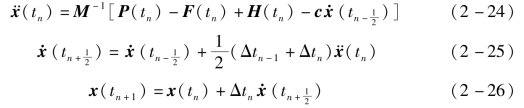
式中：
分别为tn时刻的节点加速度矢量、
时刻的节点速度矢量和tn＋1时刻的节点坐标矢量。
每一时步要计算
，必须先求得单元应力σ。它与材料模型有关，在LS－DYNA 程序中有金属和非金属材料模型近100 种，不仅要考虑应力－应变的本构关系，还要考虑材料的损伤和破坏，并且对于弹塑性材料加载与卸载过程的应力－应变本构关系也不相同，即它们的性质和时间历程有关。应力计算按时间增量进行积分：
式中：
。
若不考虑体积黏性对应力张量的影响，则有
式中：
为旋转张量；
为Jaumann 应力率；Cijkl为材料常数；
为应变率为
。
应力的具体算式可写为
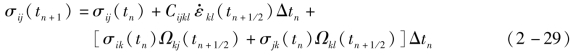
LS－DYNA 程序里将不同结构可能相互接触的两个表面分别称为主表面（节点称为主节点）和从表面（节点称为从节点）。LS－DYNA 程序处理接触－碰撞界面主要采用三种不同的算法：节点约束法、对称罚函数法和分配参数法。
节点约束法是最早采用的接触算法。它的原理是：在每一时间步长修正构形之前，检查每一个没有和主表面接触的从节点是否贯穿主表面。如果有从节点贯穿主表面，则将时间步长缩短，使那些贯穿的从节点都不贯穿主表面，而其中有的刚到达主表面。在下一个时间步长开始时，对这些从节点施加碰撞条件。对所有已经和主表面接触的从节点都施加约束条件，以保持从节点与主表面接触。此外，检查与主表面接触的从节点所属单元是否存在受拉交界面力。如有受拉面力，则用释放条件使从节点脱离主表面。
对称罚函数法是一种新的、比较简单的算法。工作原理为：每一时间步长先检查各从节点是否穿透主表面，没有穿透则对该从节点不作任何处理。如果有穿透，则在该从节点和被穿透主表面之间引入一个较大的界面接触力，大小与穿透深度、主单元表面刚度成正比，这就称为罚函数值。对称罚函数法就是同时再对各主节点处理一遍，方法和从节点一样。罚函数值大小受到稳定性限制。若计算中发生明显穿透，可以通过放大罚函数值或缩小时间步长来调整。
分配参数法一般用于仅滑动处理，工作原理为：将每一个正在接触的从单元1／2 质量分配到被接触的主表面面积上，同时由每个从单元的内应力确定作用在主表面面积上的分布压力。在完成质量和压力分配后，程序修正主表面的加速度，然后对从节点的加速度和速度施加约束，以保证从节点沿主表面运动。程序不允许从节点穿透主表面，从而避免反弹。
2.1.1.2 LS－DYNA 程序计算方法
LS－DYNA 提供了多种算法，包括Lagrange、Euler、ALE 和SPH算法［4，5］。
1.Lagrange 算法
Lagrange 算法多用于固体结构的应力应变分析，采用Lagrange 法描述的网格和分析的结构是一体的，有限元节点即物质点。采用这种方法时，分析结构形状的变化和有限单元网格的变化完全一致，物质不会在单元与单元之间发生流动。这种方法的主要优点是能够非常精确地描述结构边界的运动，但当处理大变形问题时，由于算法本身特点的限制，将会出现严重的网格畸变现象。
2.Euler 算法
Euler 算法以空间坐标为基础，使用这种方法划分的网格和所分析的物质结构是相互独立的，网格在整个分析过程中始终保持最初的空间位置不动，有限元节点即空间点，其所在空间的位置在整个分析过程始终是不变的。很显然由于算法自身的特点，网格的大小形状和空间位置不变，因此在整个数值模拟过程中，各个迭代过程中计算数值的精度是不变的。但这种方法在物质边界的捕捉上较为困难，多用于流体的分析中。使用这种方法时网格与网格之间的物质是可以流动的，即材料在一个固定的计算域中流动。欧拉网格可以理解为有两层重叠在一起，一层是空间网格，固定在空间中不动；另一层附着在材料上随材料在固定的空间网格中流动，从而可以处理流体流动等大变形问题。Euler 法有界面跟踪法、界面捕捉法等界面算法，但主要不足是边界定义不够精确，难以准确描述物质界面。
3.ALE 算法
ALE 算法兼有Lagrange 算法和Euler 算法二者的特长，即首先在结构边界运动的处理上，它引进了Lagrange 方法的特点，因此能够有效地跟踪物质结构边界的运动；其次在内部网格的划分上，它吸收了Euler 的长处，使内部网格单元独立于物质实体而存在。但是，它又不完全和Euler 网格相同，网格可以根据定义的参数在求解过程中适当调整位置，使得网格不致出现严重的畸变。这种方法在分析大变形问题时非常有利，使用这种方法时网格与网格之间的物质也是可以流动的。
4.SPH 算法
SPH 算法是近几十年发展起来的一种新的纯Lagrange 方法，其全称为“光滑质点流体动力学” （Smoothed Particle Hydrodynamics，SPH）方法。SPH方法是一种质点方法，有点类似质点网格法，但根本不同点在于SPH 方法中计算空间导数时不需要使用任何网格，而被差值公式中的解析微分式子所代替，从而避免了高维拉氏差分网格中的网格缠结和扭曲等问题。SPH 方法适用于超高速碰撞、靶板贯穿等问题。
有关高聚物黏结炸药损伤断裂的数值模拟的文章
- 详细阅读
-
PSASP软件介绍详细阅读
PSASP用户自定义程序接口功能也属于交替求解，下面对PSASP/UPI的接口原理和应用情况进行说明。如果用户在开发新程序时，能够充分利用PSASP的资源，不但可大大减少开发的工作量，缩短开发周期，而且能提高新程序的可靠性。其计算过程可用图3.1描述，设t为潮流程序和UPI交替运行的次数。图3.1PSASP主程序和UPI的连接PSASP潮流计算和UPI的接口信息提供了该UPI被多次调用的全部数据和信息。......
2023-06-29
-
Virtuoso软件介绍：界面概览详细阅读
为了使用Cadence Virtuoso设计工具，我们首先要启动Cadence Spectre的命令行窗口。最后单击“OK”按钮，弹出Virtuoso Layout Editor界面和层选择窗口，如图3.5所示。图3.2 “Library Manager”窗口图3.3 在“Library Manager”窗口的工具栏中选择File→Cell View图3.4 选择“Cell”类型为“Virtuoso”图3.5 Virtuoso Layout Editor界面和层选择窗口如图3.6所示，Virtuoso Layout Editor界面包括窗口标题栏、状态栏、菜单栏、图标菜单、光标、指针、设计区域、鼠标状态栏以及提示栏。图3.6 Cadence Virtuoso Layout Editor界面以下详细介绍Virtuoso Layout Editor界面中各部分的作用和功能。......
2023-06-26
-
介绍风资源评估软件工具详细阅读
风电场设计优化和风资源评估软件是风电场设计中相当重要的工具，从20世纪80年代开始，丹麦通过开发相应的计算机软件对风电场进行设计，目前国际上陆续开发了WAsP、WindFarmer、WindPRO、WindSIM等多种风力发电实用软件。3）用风能资源分布图推算某点的风况。......
2023-06-23
-
有限元网格及动网格模型介绍详细阅读
图6.3上止点前360°偏心轴转角计算网格初始网格建完后，转子转一圈，偏心轴转三圈，动态网格随着时间的变化发生变形及运动，为了保证计算能够正常进行，需要不断对网格进行更新。通过宏命令DEFINE_GRID_MOTION和DEFINE_CG_MOTION定义网格的运动规律，网格更新方式采用弹簧光顺和网格重构相结合的方式。......
2023-06-23
-
MVC软件开发架构的优点及介绍详细阅读
MVC 软件开发架构的优点如下：分工明确：使用MVC 软件开发架构可以把数据库开发、程序界面开发、程序业务逻辑开发有效分离，以安排不同的人员完成不同的任务，分工合作完成总体任务。本章及以后两章将针对MVC 软件开发架构的模型、控制器、视图的相关内容分别作介绍。......
2023-11-25
-
网格划分和有限元分析实例|SAMCEF软件应详细阅读
单击Mesh模块图标，进入网格划分模块，相应的工具条中显示出网格处理的命令。设置Average Mesh Size为6，单位为mm。单击Apply按钮，生成二维轴对称单元，总计2078个单元，2945个节点，有限元模型如图14-199所示。单击右键，在弹出菜单中选择Mesh Aspect→Shade命令，有限元网格着色显示如图14-199所示。图14-199 有限元网格3.保存文件单击工具条中的保存文件快捷图标。......
2023-10-27
-
连接类型介绍-SAMCEF有限元分析实例详细阅读
不同的分析也有各自适用的连接类型，如非线性分析中的转动铰，转子分析中常用的轴承等。表5-1所列的是比较常用的装配连接类型。在类似的情形下，需要考虑间隙缩减量，其单位与当前使用的单位一致。如果需要，还可以定义一些高级控制参数进行操作。图5-56 粘接定义对话框高级控制参数如下。......
2023-10-27
相关推荐