图6-36为作者采用水基切削液、自然环境和低温风三种冷却条件下,以49m/min、f=0.15mm/r的工艺参数切削轴承钢,得到不同冷却方法切削力对比曲线。......
2025-09-29
1.铣削时切削温度的经验公式
在铣削加工环境固定不变的前提条件下,切削温度与切削参数之间存在复杂的指数关系。铣削时切削温度的经验公式的通用形式是
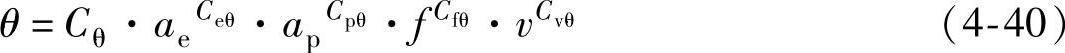
式中,Cθ是切削温度系数;Ceθ、Cpθ、Cfθ和Cvθ分别是切削宽度、切削深度、进给量和切削速度的指数。
2.确定因子的变化范围
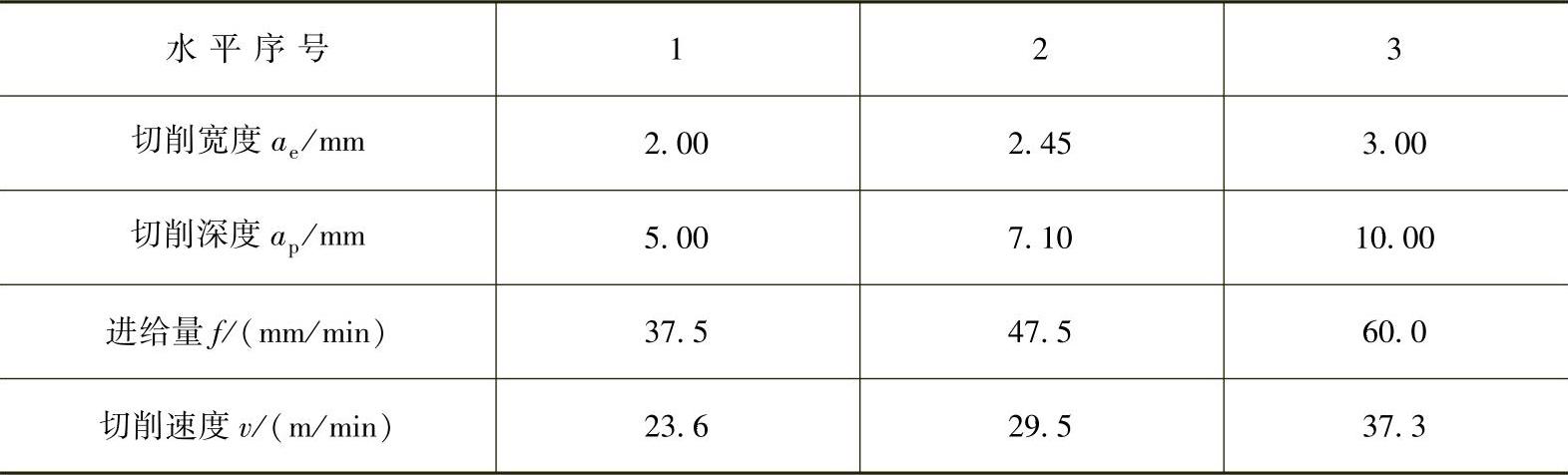
由上述经验公式可知,影响切削温度的四个因素是:切削宽度、切削深度、进给量和切削速度。因为加工难加工材料受到工艺装备、设备条件等多方面条件的制约,所以切削数据来源于生产现场或由技术人员提供,见表4-6。这里分别给每个因素三个水平,综合考虑后选用L9(34)正交表。
表4-6 四因素实验水平的选取
3.各因子水平的编码
分别通过线性变换
Z1=(lgae-0.39)/0.090 (4-41)
Z2=(lgap-0.85)/0.15 (4-42)
Z3=(lgf-1.68)/0.10 (4-43)
Z4=(lgv-1.47)/0.10 (4-44)
可以得到四个因素取对数后的三水平的编码。程序自动计算,得到各因素的零水平、区间值以及三水平的编码表,见图4-14。
4.实验数据的获取
按切削实验表中的方案进行切削实验(红外线测温图见图4-15)。
由于采用的是间接获得切削区的温度,所以实验测量区温度与切削区温度需要进行换算。
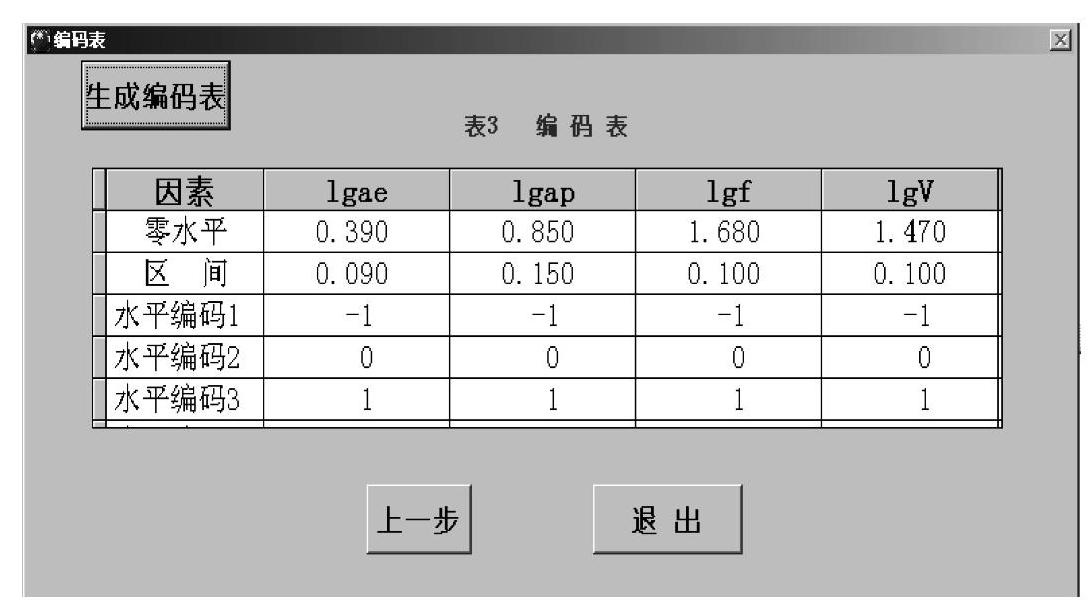
图4-14 编码表(https://www.chuimin.cn)

图4-15 铣削时测量面处红外线测温图
傅里叶定律的热流密度公式是

式中,λ是导热系数[W/(m·℃)]; 是温度的变化率(℃/m)。
是温度的变化率(℃/m)。
设切削热由切削区传导δ距离至测量面,铣削区的最高温度为θm经试件传递到试件测试面后温度降为θs,并假定在热流流动方向上的任意截面单位面积上的导热量相等,通过对式(4-45)求积分得到下式:

式中,θm为最高温度;θs为测试面后温度;δ是切削区传导至测量面的距离。又试件测量面上发出的辐射能是
E=q=εσT4 (4-47)
式中,ε是测温面的辐射率;σ是斯蒂芬·玻尔兹曼常数,σ=5.67×10-8;T是物体辐射单元的热力学温度。由式(4-46)和式(4-47)可以推导出下式:
θm=θs+εσT4δ/λ (4-48)
所以,将获取测量面的温度值、切削面与测量面的厚度代入式(4-48),即可得到铣削区的最高温度值。在切削温度的测量中使用了黄色漆,以增加辐射表面的辐射率。其测温面的辐射率经测定为ε=0.92。
通过测试系统得到切削温度经由式(4-48)计算得到的切削区温度的测试数据见图4-16。
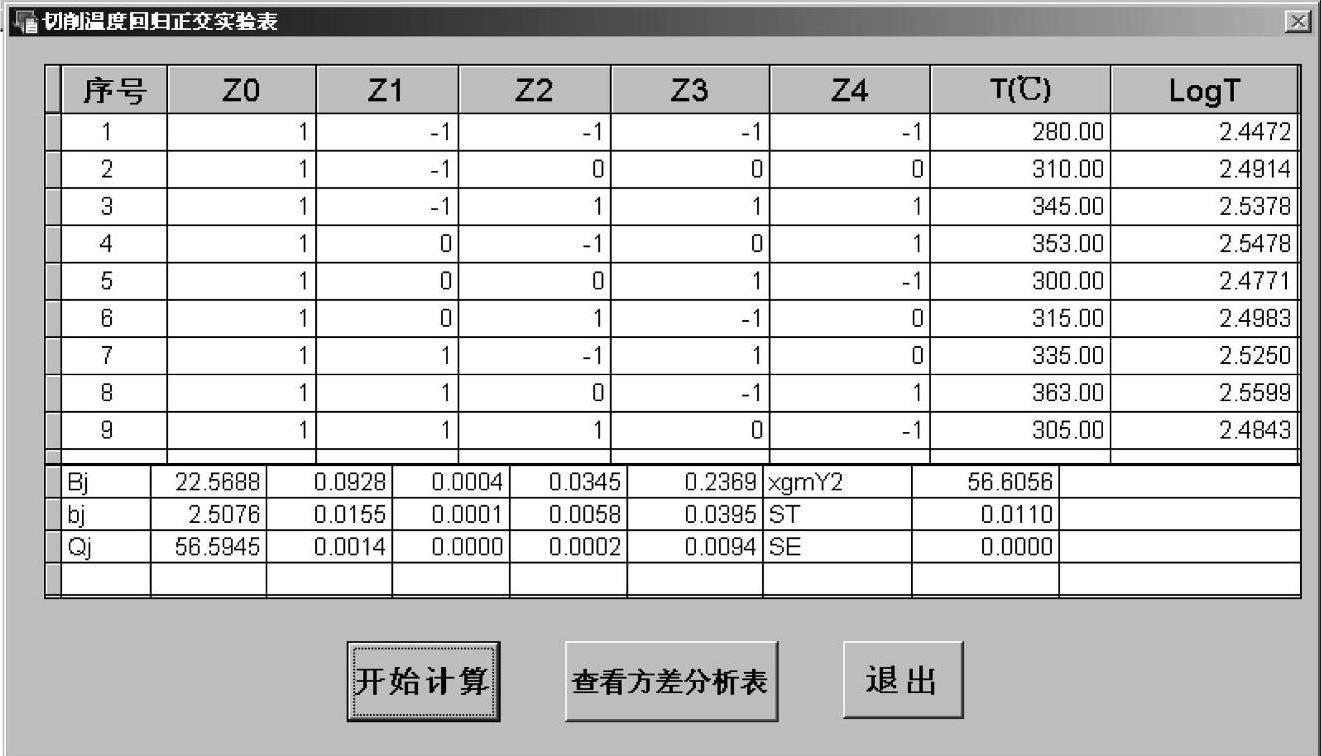
图4-16 切削温度数据及处理结果
5.实验结果
使用最小二乘法对实验数据进行统计处理后,得到切削温度与各切削用量的线性回归模型:
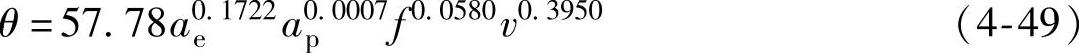
相关文章

图6-36为作者采用水基切削液、自然环境和低温风三种冷却条件下,以49m/min、f=0.15mm/r的工艺参数切削轴承钢,得到不同冷却方法切削力对比曲线。......
2025-09-29

由于干切削存在上述现象,所以对干切削机床的要求和使用与湿式切削有所不同。干切削机床必须具有良好的散热、排屑及吸尘装置和具有良好刚性的基础部件。1)干切削机床应有较高的刚性,以避免加工中产生振动。3)干切削机床应尽可能是高速机床,这种机床可降低30%左右的切削力,95%以上的切削热可由切屑带走,工件可基本保持室温状态。......
2025-09-29

且此类节点越多,病毒就越容易传播,确诊人数也会增加得越快。因此,控制这些地理节点是阻止新一轮病毒传播的有效方法。通过控制几个社区间的紧密联系路径与关键地理节点,可以有效地防止社区间的交叉感染,阻止新一轮病毒的传播。......
2025-09-29

图1-11 切削力的分解主切削力Fc是总切削力在主运动方向上的分力。这是由于ap增大时单位切削力基本不变,f增大时单位切削力减小。F增大时hD增大,切屑底层的剧烈变形层占整个切削层的比例减小,使平均变形程度下降,Fc随着进给量f的增大而减小。切削速度对切削力的影响因材料不同而异。切削功率为切削力Fc和进给力Ff所消耗功率之和。......
2025-09-29

通常要求T0=0℃,但在实际使用中要做到这一点比较困难,因而产生了热电偶冷端温度补偿问题。当冷端温度升高时,RCu值随之增大,电桥失去平衡,Uab相应增大,此时热电偶电势Ex由于冷端温度升高而减小。桥臂RCu必须和热电偶的冷端靠近,使它们处于同一温度之下。......
2025-09-29

图12-57 控制系统网络断线时的切换请求图12-59 用户切换允许标志SM1592置ON点击“执行”按钮后,出现确认对话框,点击“是”按钮,如图12-61所示。图12-65 系统不能切换时PLC诊断点击“帮助”菜单,查看错误代码一览表,从中找出错误的原因及对策,如图12-66所示。......
2025-09-29

提高切削速度、加大进给量和背吃刀量,都使得单位时间内金属的切除量增多,因而都有利于生产率的提高。根据工件材料和刀具材料确定切削速度,使之在已选定的背吃刀量和进给量的基础上能够达到规定的刀具寿命。......
2025-09-29

通过对上述各种状况下的最大和最小制动力矩的分析和反复验算,可制定一个既能满足制停距离要求,又能符合最大减速度规定的附加制动器制动力矩Taux,作为附加制动器具体结构设计参数。......
2025-09-29
相关推荐