表7.3-1长江干流2003—2006年不同河段冲淤量实测值与验证值对比注 表中负值表示河道冲刷。洞庭湖区采用2003年四口河系地形资料和2006年长江干流和洞庭湖湖盆地形资料，对模型进行验证计算。......
2023-06-21
热-力耦合模型优化方案
【摘要】：所以，对于切削加工过程中温度和应力的耦合问题，需要按热-力耦合的方法求解。工件还受到外部节点力载荷和分布载荷及体力载荷作用，总的等效节点力为式中，Δ{R}ed、Δ{R}ep、Δ{R}eF分别是外部节点力载荷、分布载荷和体力载荷的等效节点力。
在金属切削加工过程中，工件在产生塑性变形的同时伴随着温度的变化，即金属切削时材料的塑性变形以及刀具与切屑、已加工表面的剧烈摩擦会使切削变形区域的温度在瞬间剧升。由于温度变化对工件变形和材料的力学性能会产生影响；同时，工件的切削变形反过来也会改变热边界条件，进而影响温度场。所以，对于切削加工过程中温度和应力的耦合问题，需要按热-力耦合的方法求解。
为了耦合切削加工过程中热载荷和机械载荷之间的相互影响，根据Prandtl-Re-uss理论，考虑到全应变增量包含弹性应变增量、塑性应变增量和温度应变增量，即可得热弹塑性力学本构关系：
弹性区：d{σ}=[D]（d{ε}-d{ε}T） （3-27）
塑性区：d{σ}=[D]（d{ε}-d{ε}T-d{σ}T） （3-28）
式中，Δ{α}表示工件材料的线胀系数；[D]、[D]ep分别表示弹性矩阵和弹塑性矩阵；T表示温度；
表示等效应力。
由于热弹塑性材料的应力应变关系是非线性的，可以用“增量载荷法”将此关系线性化处理。
弹性区：Δσ=[D]（Δ{ε}-Δ{ε}T） （3-29）
塑性区：Δσ=[D]ep（Δ{ε}-Δ{ε}T）+Δ{σ}T （3-30）
式中，Δ{ε}T、Δ{σ}T分别为初应变和初应力。
弹性区：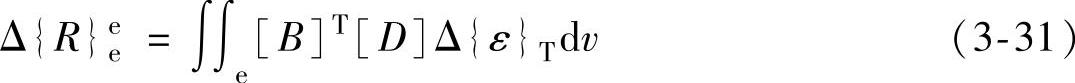
塑性区：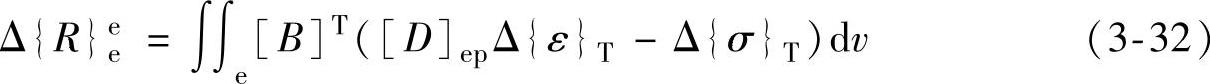
式中，Δ{R}ee为应变矩阵。
工件还受到外部节点力载荷和分布载荷及体力载荷作用，总的等效节点力为
式中，Δ{R}ed、Δ{R}ep、Δ{R}eF分别是外部节点力载荷、分布载荷和体力载荷的等效节点力。
总的平衡方程式是
[K]Δ{u}={ΔR} （3-34）
式中，[K]为总体刚度矩阵；Δ{u}为节点位移增量。
有关沉淀硬化不锈钢的切削与数值模拟的文章
- 详细阅读
-
如何优化切削力和切削热？详细阅读
图1-11 切削力的分解主切削力Fc是总切削力在主运动方向上的分力。这是由于ap增大时单位切削力基本不变，f增大时单位切削力减小。F增大时hD增大，切屑底层的剧烈变形层占整个切削层的比例减小，使平均变形程度下降，Fc随着进给量f的增大而减小。切削速度对切削力的影响因材料不同而异。切削功率为切削力Fc和进给力Ff所消耗功率之和。......
2023-06-26
-
耦合模型和非耦合模型的计算成果对比分析详细阅读
图11.11降压结束时水平截面主应力等值线图表11.2耦合非耦合模型计算应力和位移特征值（最大值）比较高压压水引起岩体发生较大位移量的范围约为3.0m，远远小于渗流应力耦合作用模型条件下13m的范围。图11.12为试验区特征铅直剖面上的第三有效主应力等值分布图。由图11.12可知，按流固耦合模型计算得到的应力场分布形态与非耦合模型计算得到的应力场分布形态有显著的差别。......
2023-06-28
-
热流固耦合模型探讨详细阅读
为研究传热、水流和力学等参数的横观各向同性耦合效应，采用FLAC3D软件对该地下岩石实验室中的黏土岩的热流固耦合效应进行了数值仿真模拟。图12.3热-流-固耦合关系图温度改变引起的有效应力通过改变计算模型的应变量来实现；孔隙压力对有效应力的影响由太沙基有效应力原理来计算。计算采用的黏土岩热-流-固耦合关系见图12.3。......
2023-06-28
-
热回流的理论分析及优化方案详细阅读
对测量反馈输入与PID输出变化率监控，输出相应报警。图2.4带挡风墙的空冷换热器的流动示意图式中vj——蒸汽分配管出口平均速度，方向沿竖直向上，并且假设速度大小在离开挡风墙前后保持不变。下式给出有风条件下与无风条件下热回流的关系，即①PID输出变化率监控与PID输出限制值设定参数相同，2种功能不能同时选择。式从理论上很难分析热回流的大小，只能通过模型试验、数值模拟和现场测试的方法来得到。......
2023-06-24
-
爆裂毁伤模型优化方案详细阅读
同时，冲击波传入靶体，在径向产生压应力和应变，在切向产生拉应力与应变。由于混凝土靶体材料的抗拉强度远低于抗压强度，因此靶体首先在拉应力作用下发生断裂，形成径向裂纹。气体产物沿裂纹区扩散，导致裂纹进一步扩展，造成本体功能型硬目标结构爆裂毁伤。图6.33混凝土靶爆裂毁伤计算模型混凝土靶体中最终裂纹长度取决于高压气体产物膨胀，而爆燃压力直接取决于进入侵孔内活性材料的质量。......
2023-06-18
-
建模车削力的优化方案详细阅读
图4-7 编码表正交表与测试数据及其处理结果5.实验数据的获取按切削实验表中的方案进行切削实验，通过测试系统分别得到Fx、Fy和Fz三个方向切削力的值，测试模拟信号见图4-8，数据见图4-7。......
2023-06-27
-
模型参考自适应控制优化方案详细阅读
图3-24所示为设计的模型参考自适应控制方案。那么图3-24 模型参考自适应控制方案可得自然频率wn=30rad/s，调节时间ts≈3.15T1≈0.25s，同时得到参考模型的两个极点-12.6061和-71.3939。为达到控制目标，自适应控制器输出由系统模型定义为Dδ=KT·xδ+θT·r 式中，K=[K1，K2]T和θ分别为闭环系统的反馈增益和前馈增益。上式代入单相并联型APF动态模型式，得定义跟踪误差e=xδ-xm 这里的控制目标为找到一个自适应控制律使跟踪误差e趋近于0。......
2023-06-23
相关推荐