这些因素包括：1.时间点冲突开始发生时刻的标志。对于建模而言，则是能够得到有用信息的终点。在冲突模型中，这些具有独立决策权的参与者被称为决策人，或局中人。我们称只含有两个决策人的冲突模型为“二人对策”，而多于两个决策者的冲突为“多人对策”。偏好函数在冲突分析中起着非常重要的作用，也是模型化过程中最重要的一步。......
2023-07-15
刀具与工件的接触法则优化：关键要素解析
【摘要】：2.刀具前刀面与切屑分离以及后刀面与已加工表面的分离准则在刀具的前刀面与切屑、后刀面与已加工表面接触的节点上作用一个拉力，该节点就必然与接触面分离。
1.刀具前刀面与切屑界面接触摩擦模型
在刀具-切屑界面之间存在着复杂的非线性接触问题，但为了数值模拟方便起见，一般将其简化处理成两种不同机制的摩擦区域，即黏着区和滑动区，如图3-1所示。其中，黏着区的摩擦力大小维持恒定，而滑动区的摩擦力大小则可以用库仑模型进行描述。
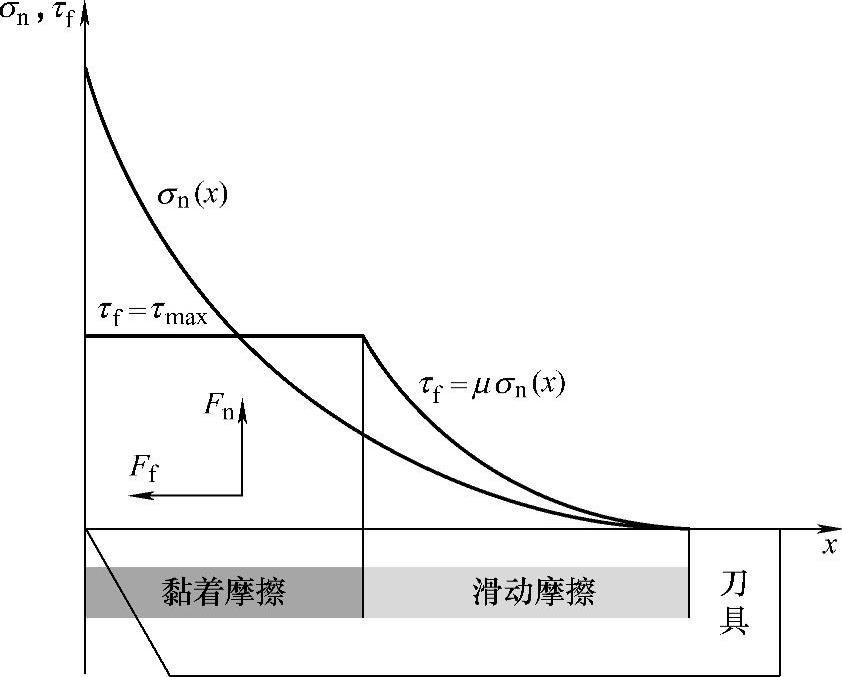
图3-1 刀具-切屑界面法向应力σn和切向应力f的分布
（1）滑动区的摩擦应力 根据库仑摩擦理论，接触表面滑动摩擦区的切向滑动摩擦力Ff与法向正压力Fn有如下关系：
式中，f为切向（摩擦）应力（MPa）；σn为接触节点处的法向应力（MPa）。
（2）黏着区的摩擦应力 当工件与刀具表面没有相对滑动，完全处于黏合状态时，此时摩擦剪应力为
f≤mσcrit （3-18）
式中，m为摩擦系数（取值范围0～1.0）；σcrit为接触节点处的法向应力（MPa）。
假定材料符合von-Mises屈服准则，则最大许可剪应力crit为
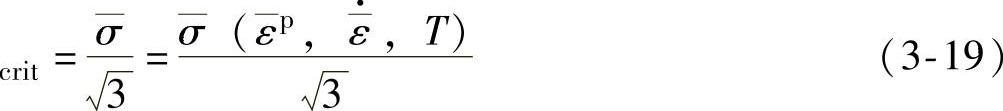
式中，
表示屈服应力（MPa）。
（3）过渡区的摩擦力 由于切屑与刀具前刀面的摩擦由黏着摩擦过渡到滑动摩擦，摩擦应力随相对滑动速度值产生阶梯函数状的变化。在数值模拟中，由于这种不连续，会造成数值计算困难。因此，引入一个过渡区摩擦模型，公式是
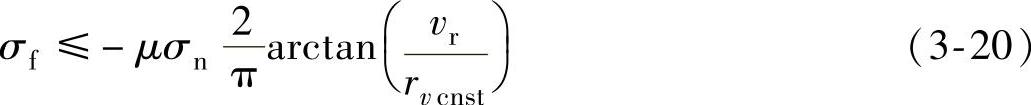
式中，rvcnst表示发生滑动时接触体之间的临界相对速度（m/s）；vr表示接触点相对滑动速度（m/s）。
为了真实地模拟前刀面与切屑的摩擦，克服由黏着摩擦到滑动摩擦的摩擦应力的突变，可选用新的库仑摩擦模型（基于节点力）。黏-滑阶跃摩擦见图3-2。
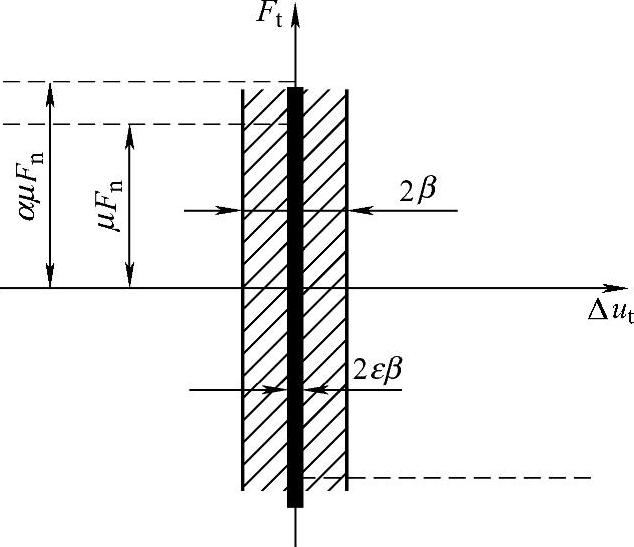
图3-2 黏-滑阶跃摩擦
图中，Δut为切向量位移增量；α为因子（一般取1.05）；β为黏着摩擦到滑动摩擦的相对位移过渡区域（一般取10-6mm）；ε为小常数，因此εβ≈0。
2.刀具前刀面与切屑分离以及后刀面与已加工表面的分离准则
在刀具的前刀面与切屑、后刀面与已加工表面接触的节点上作用一个拉力，该节点就必然与接触面分离。从理论上说，接触节点的反力为零时恰好分离。但实际数值的处理中，由于各节点的力平衡方程不能精确地满足所造成的误差，可能在分离时节点上仍有一个较小的正反力存在。这就需要设置一个引起接触节点发生分离的最小节点反力。这个门槛值同时也可避免接触点发生不必要的分离。
当分离发生时，这一对接触反力如同残余力（作用在自由节点上的零外力）。这时就必须释放其接触反力，这样才能减少计算过程的迭代次数。
有关沉淀硬化不锈钢的切削与数值模拟的文章
- 详细阅读
-
如何选择合适的刀具：接触式和非接触式识别装置详细阅读
图6-26 刀具编码示意图1—编码环 2—编码识别装置 3—锥度7∶24锥柄 4—触针 5—锁紧螺母 6—拉钉刀具编码任意选刀方式中的刀具识别装置有接触式识别装置和非接触式识别装置两种，而非接触式识别装置根据选用的识别材料不同，又可分为非接触式磁性识别装置和非接触式光电识别装置两种。......
2023-06-23
-
刀具切削部分的构成要素详细阅读
车刀的切削部分由三个表面、两条刀刃和一个刀尖组成。通常以圆弧或短直线形出现，以提高刀具的使用寿命。为了改善刀尖的切削性能，常将刀尖做成修圆刀尖或倒角刀尖，如图2－7所示。图2－7刀楔、刀尖形状参数不同类型的刀具，其刀面、切削刃数量不同，但组成刀具的最基本单元均是两个刀面汇交形成的一个切削刃，简称两面一刃。......
2023-07-01
-
高压喷射灌浆施工的关键要素及优化方法详细阅读
（一） 孔距及布置形式孔距及布置形式的设计合理与否，对高压喷射灌浆的造价及质量影响很大。表13-3高压喷射灌浆固结体特性指标（二） 施工工艺技术参数高压喷射灌浆质量的好坏、工效和造价的高低，不仅受工程类型、喷射地形及地质地层条件的影响，更重要的是取决于施工工艺技术参数的合理选用。表13-4高压喷射灌浆主要工艺技术参数表（三） 施工流程高压喷射灌浆施工流程见图13-16。......
2023-06-29
-
综合要素分析法：优化企业决策的关键详细阅读
严格地讲，综合要素分析法没有一定的格式，具有很大的灵活性，但同时要结合注塑件形体“六要素”的分析和注塑模结构方案可行性分析的常规分析法。综合分析法由若干个要素的常规分析法组成，可分成多重要素综合分析法、多种要素综合分析法和混合要素综合分析法三种。......
2023-06-30
-
环保旅游业的关键要素详细阅读
绿色旅游管理一般与国家发展水平一致，所以德国、美国、加拿大和澳大利亚、日本等国家的旅游业绿色管理的现状较好。国家公园事业已经成为全人类普遍认同的文明社会的公益事业。在格莱莫吉恩斯国家公园，要求游客带走自己产生的废弃物。为此，加拿大政府组织专家研究并应用了旅游卫星账户，试图通过建立一套虚拟的国民账户，反映旅游业活动的全景。......
2023-11-22
-
刀具交换方式优化方案详细阅读
刀具交换机构的具体形式和交换方式对数控机床的生产率和工作可靠性有着直接的影响。通常，刀具交换方式可分为无机械手换刀和机械手换刀两大类。其典型代表为斗笠式刀库的自动换刀。......
2023-06-23
-
切屑与工件分离的准则优化详细阅读
已经提出的切屑分离准则分为两种类型，即几何准则和物理准则。切屑分离准则只有真实反映工件材料的力学和物理性质，才能得到合理的有限元模拟结果。另外，当工件材料确定后，一个最佳的分离准则是其临界值不应该随着切削条件的不同而改变。失效应力准则表示为式中，σn、n分别是切屑和工件分界面上单元的正应力和剪应力；σs、s分别是正应力和剪应力的阈值。......
2023-06-27
相关推荐