图5-107控制体积法节点布局示意图5.5.3.2泥沙方程离散和求解悬移质输运方程离散和求解。悬沙输运方程和水流模型中的k、ε方程形式基本相同，只是在悬移质输运方程中多了一个下沉项，试算表明将下沉项作为源项比作为对流项更有利于求解的稳定。模型采用修正的QUICK 格式来离散悬沙输运方程的对流项，求解离散方程也采用ADI方法，相对于高阶格式所产生的离散方程的多余附加离散项采用显式离散，不存在求解困难。推移质输运方程的离散和求解。......
2023-06-22
通用离散方法下的方程求解
【摘要】：引入通用变量φ，将偏微分方程组式～为通用形式，并利用高斯定理在控制体积中离散，最终得到如下方程形式：式中：Гφ为通用扩散系数；Sφ表示源项。对时变项采用一阶差分格式离散，扩散通量采用超松弛校正方法计算，界面处梯度（▽φ）f由线性插值得到。于是单元面处通量可以表示为：式中：F f＝f；（φf）H为高阶部分，可以表示为：最终的方程离散形式如下：式中：；上标n为前一时间步长；下标P为当前控制体积。
引入通用变量φ，将偏微分方程组式（1）～（4）为通用形式，并利用高斯定理在控制体积中离散，最终得到如下方程形式：
式中：Гφ为通用扩散系数；Sφ表示源项。
对时变项采用一阶差分格式离散，扩散通量采用超松弛校正方法计算，界面处梯度（▽φ）f由线性插值得到。为改善非结构网格下对流项通量的计算精度，本文引入在均分网格中具有三阶计算精度的QUICK格式，同时利用DAVIDSON［4］提出的折中思想，重构远上风点。具体构造过程如下：如图1所示，远上风点U是由相邻单元中心
的连线和其对应的单元面交点构成。该点处的变量值可以利用变量在单元中心P的泰勒级数展开获取，计算方法如下：
图1 QUICK格式远上风点的构造
（a）
·
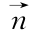＞0；（b）
·
＜0
为简单起见，仅取上式右端前两项，做二阶近似处理。然后利用QUICK格式的插值方法对界面f处的变量值φf进行估算，具体又分为以下两种情况：
情况1：
式中：f 1＝－（z－y）（y－x）/xz；f 2＝y（y－x）/z/（z－x）。
情况2：
式中：f 3＝－（z－y）（y－x）/xz；f 4＝y（y－x）/z/（z－x）。
计算中将低阶对流项通量整合到方程组左边作隐式处理，高阶项部分作为源项作显格式迭代，从而可以保证计算矩阵的主对角元占优，这样可大大提高计算的稳定性能。于是单元面处通量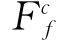
可以表示为：
式中：F f＝（ρH A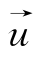
·
）f；（φf）H为高阶部分，可以表示为：
最终的方程离散形式如下：
式中：
；上标n为前一时间步长；下标P为当前控制体积。
为了进一步提高计算的稳定性，引入欠松弛系数αP，于是公式（12）可以改写为：
有关中国环境与生态水力学（2008）的文章
- 详细阅读
-
矩阵方程AX=B的求解方法详细阅读
【主要内容】设A是m×n矩阵，B是m×l矩阵，它们都是已知矩阵，X是未知矩阵，则称方程AX=B为矩阵方程.满足AX=B的矩阵X称为该方程的解.设A=（A┆B），称为该矩阵方程的增广矩阵，则AX=B有唯一解的充分必要条件是，AX=B有无穷多解的充分必要条件是，AX=B无解的充分必要条件是注 （ⅰ）矩阵方程AX=O（其中，A是已知的m×n矩阵，O是m×l零矩阵）有非零解的充分必要条件是r（A）
2023-10-27
-
根轨迹方程的求解方法详细阅读
系统的闭环特征方程为取其模值得模值方程为取其相角得相角方程为模值方程和相角方程成为根轨迹方程，从这两个方程可以看出，模值方程与增益K*有关，而相角方程与增益K*无关。所以，相角方程式决定闭环根轨迹的充分必要条件，而模值方程主要用来确定根轨迹上各点对应的开环增益值。，sn为闭环极点，在根轨迹图中用Δ表示。......
2023-06-28
-
控制方程求解的方法与优化详细阅读
式即为动态分析中实际求解的有限元代数方程组。由于式考虑了渗透张量与应力的耦合关系，即使采用弹性本构模型，式也是一个非线性方程组，仍需在每一个计算时步内迭代求解。当然与式相比，式消除了自由面边界非线性的影响，非线性仅来源于随应力的变化，非线性程度减弱了，因此数值分析的计算量也减小了，收敛性也可以保证。......
2023-06-28
-
单相流的连续方程求解详细阅读
在流场中任取一个控制体Ω，该控制体内有多孔固体介质，孔隙度为φ。多孔介质被流体所饱和。在控制体内任意取一体元dΩ进行研究。在多孔介质不变形的情况下，孔隙度φ保持恒定，则φ可从偏导数中分离出来。式是非稳态有源流动连续性方程的一般形式。根据三维达西流方程，有当域内不存在源或汇时，非稳态渗流的连续性方程转化为对于流体不可压缩情形，连续性方程转化为......
2023-06-28
-
叶片泵设计数值通用对流扩散方程的有限体积离散详细阅读
回代入原通量密度式得其中Fe=，令aE=∣DeA∣，有Je=p-aEE 类似可得Jw=aWW-p 对南北方向类似地有Jn=p-aNN Js=aSS-p 将以上四项回代入原式得aPP=aEE+aWW+aNN+aSS+b 对界面上函数及其导数采取特定的构造格式，即确定了系数A和B的具体形式，就可以获得最终的离散表达式。......
2023-06-26
-
高等数学：欧拉方程的求解方法详细阅读
变系数的线性微分方程，一般说来都是不容易求解的.但是有些特殊的变系数线性微分方程，则可以通过变量代换化为常系数线性微分方程，因而容易求解，欧拉方程就是其中的一种.形如的方程（其中，p1，p2…pn为常数），叫做欧拉方程.作变换x=et或t=lnx，将自变量x换成t，有如果采用记号D表示对t求导的运算，那么上述计算结果可以写成一般地，有xky=D（D-1）…......
2023-11-22
-
参数方程导数求解方式或者函数导数：参数方程求详细阅读
1）参数方程确定的函数的导数有时函数由参数方程来表示更方便且简单，如π）表示以R为半径、原点为圆心的上半圆周曲线.星形线的直角坐标方程为其参数方程为显然星形线的参数方程更为简单.一般地，设参数方程若t∈（α，β）时，x＝x（t），y＝y（t）都有连续的导数，且x′（t）≠0，可以证明x＝x（t）必有单值反函数t＝t（x），代入y＝y（t）中，得y＝y［t（x）］，因此在所给条件下，参数方程确定了y......
2023-11-19
相关推荐