观察图7可以发现，Path2 分布着压应力与拉应力两种残余应力形式，在0～0.3 mm 的路径范围内，残余应力形式为拉应力，在0.3～4.4 mm 的路径范围内，残余应力形式为压应力，残余压应力占据了更多的路径区间；在距离路径起始点0.22 mm 与0.44 mm 的位置，存在着与路径其他区域相比更大的残余应力突变，这些应力突......
2023-06-23
二维模拟结果中污染云团纵向拉伸速度的变化趋势与分析
【摘要】：随着时间发展，二维模拟结果中，污染云团的纵向断面平均浓度分布趋于正态。表4污染物进入水体后的传播特征若定义，v具有速度量纲，可用来表征污染云团纵向长度变化的快慢，本文称为云团的纵向拉伸速度。图4污染云团纵向拉伸速度随时间变化过程线计算实践表明二维模型能相当准确地模拟污染物在射流区的三维输运过程，所以可认为二维模拟结果中污染云团的纵向拉伸速度沿理论曲线ABCE随时间变化。
（1）一维和二维模拟结果的比较。由图1～图3中的结果可见，一维和二维模型都能模拟污染云团在水体中的平均移动速度，其值等于渠道中的平均流速。
表3 各工况不同时刻最大浓度（mg/L）
注 一维模拟结果中，浓度指断面平均值；二维模拟结果中，浓度指深度平均值。
二维结果中，污染云团浓度纵向呈扭曲的偏态分布；一维模拟结果中，由于忽略了初期混合过程，断面平均浓度纵向呈正态分布，最大断面平均浓度点比二维模拟的结果滞后。随着时间发展，二维模拟结果中，污染云团的纵向断面平均浓度分布趋于正态。
根据Saffman等人［6］的研究，污染物进入水体后的传播过程，可以分为射流核心区、扩散区和离散区，各分区污染云团断面平均浓度纵向分布的方差σ2x随时间t的变化规律见表4。
表4 污染物进入水体后的传播特征
若定义
，v具有速度量纲，可用来表征污染云团纵向长度变化的快慢，本文称为云团的纵向拉伸速度。由三个分区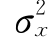
和t的关系，本文首次推导出v随时间变化的曲线如图4中实线ABCE所示。
图4 污染云团纵向拉伸速度随时间变化过程线
计算实践表明二维模型能相当准确地模拟污染物在射流区的三维输运过程，所以可认为二维模拟结果中污染云团的纵向拉伸速度沿理论曲线ABCE随时间变化。当采用一维模型时，忽略了射流区和扩散区的影响，认为污染物的输移扩散规律满足离散区的规律，所以污染云团的纵向拉伸速度沿曲线DCE随时间变化。速度变化曲线与时间轴之间围成的面积表示污染云团的纵向长度，所以二维模型模拟所得污染云团长度应比一维模型短。图1～图3中的模拟结果，既印证了模拟过程的准确性；又表明，对于该处渠道，在10km左右范围内非常有必要采用水平二维模型模拟污染物的输移扩散过程。
（2）投放历时对污染物运动的影响。对比工况2和工况1的计算结果可见，当污染物进入水体的速度加快时，一维和二维模型的计算结果之间的差别更加明显，同时，侧边和中心事故所形成浓度场之间的区别也更加明显。这是因为污染物排放时间较长时，纵向对流作用使污染云团纵向浓度分布趋于均匀，所以，污染物排放的时间越短，越有必要采用二维数值模型模拟污染物的输移扩散规律。
（3）污染物投放点横向位置的影响。在梯形渠道中，渠道边缘附近水深很小，侧边的反射作用减弱；同时，渠道边坡增大了纵向流速的横向梯度，提高了边壁附近的紊动混合系数和剪切作用，从而加快了污染物的混合过程［7］。由表3中二维模型的模拟结果可见，由于中心处水深较大，污染物以同样的接触面积从渠道中心进入水体，形成初始浓度场最大浓度小于污染物从渠道侧边进入时的最大浓度。但由于边坡的影响，后者最大浓度值衰减更快，同时，由图1～图3可见，后者断面平均浓度的纵向分布更快地趋于正态分布。
（4）横向混合作用的影响。对比表3中的结果可见，横向混合作用加剧后，渠道侧边发生的事故和中心事故形成的浓度场之间的差别大大减小。同时，由图1～图3和表3可见，横向混合系数增大后，二维模拟所得污染物断面平均浓度纵向分布更快地趋于正态分布，一维和二维模型模拟所得污染云团的纵向长度之间的差别变小。
在扩散区，污染物混合速度与横向混合系数呈正相关关系，在离散区呈负相关关系，横向混合系数增大后，扩散区污染物的扩散加剧，离散区的纵向离散作用减弱，污染云团纵向拉伸速度随时间的变化曲线，变成图4中虚线所示。一维和二维模型纵向拉伸速度曲线所围成的面积，表示两种模型模拟所得污染云团纵向长度的差值，与横向混合系数增大前相比，一维和二维模拟结果之间的差别缩小，这正与数值模拟的结果吻合。
有关中国环境与生态水力学（2008）的文章
- 详细阅读
-
动态拉伸计算结果的分析与优化详细阅读
然而，随着颗粒体积分数的增大，炸药的脆性增加，更容易发生拉伸破坏。模型一、模型二和模型三的破坏应变分别为0.8%、1.3%、1.39%。图8－35三种不同颗粒体积分数和颗粒分布细观结构模型的应力－应变曲线图8－36～图8－38 所示为三种细观模型在动态拉伸载荷下的损伤破坏过程。从三种模型的计算结果可以发现，动态拉伸作用下PBX 的损伤机理主要是界面脱黏和黏结剂撕裂。......
2023-06-27
- 详细阅读
-
单轴拉伸计算结果分析详细阅读
我们注意到，单轴拉伸下的失效应变仅为0.004 1，说明PBX 9501 是一种脆性材料。图8－20应变率为10－3s－1时的单轴拉伸应力－应变曲线图8－21 所示为应变为0.16%、0.41%、0.45%和0.5% 时的Y 方向应变云图和损伤断裂演化图。从图中可以看出，整个拉伸过程黏结剂承受了大部分的变形。该结果表明PBX 9501 的拉伸力学性能与界面黏结强度有关，而失效路径与界面强度无关。......
2023-06-27
-
半圆盘弯曲实验模拟结果分析详细阅读
对不同预制裂纹长度的半圆盘实验进行有限元建模分析。图4－7 所示为预制裂纹长度为0.96 mm 时，实验及数值模拟得到的载荷－位移曲线。从图中可知，计算结果和实验结果吻合较好，说明黏聚裂纹模型适用于半圆盘弯曲实验的力学性能分析。......
2023-06-27
-
计算结果和分析-多尺度模拟与分析研究详细阅读
作为展示，图6.10和图6.11给出了其中尺寸为H＝50mm和H＝200mm的试样的模拟结果。对图6.12中的荷载－跨中位移计算结果进行处理，得到不同尺寸下混凝土梁的跨中最大应力（强度）和相对挠度的关系曲线如图6.13所示。表6.1梁跨中名义强度与断裂能的尺寸效应有关混凝土梁损伤演化分析的更多结果及其分析，有兴趣的读者可参阅参考文献［26］中的相关章节。......
2023-08-26
-
纵向分布特征：速度场和浓度场详细阅读
对于盐水入侵问题，速度场和盐度场的纵向分布是重点关心的问题，下面将对计算结果反映出来的特征做重点的分析，图4给出了后面分析将要提到的5种工况的速度场和浓度场。底部盐度sb和表层盐度ss之差与se的比值表示分层系数。......
2023-06-26
-
二维铣削加工的数值模拟运行实例详细阅读
建模系统的运行界面见图5-11。从图5-14可以看出，仿真值与实验值比较接近，相对误差都在10%以内。图5-14 铣削过程中切削力和切削温度的仿真值与实验值a）切削力的仿真值与实验值 b）切削温度的仿真值与实验值......
2023-06-27
相关推荐