K～ZC的基本偏差为上极限偏差ES，其值为负值，且从K～ZC基本偏差的绝对值依次增大。当图样上给出的是公差带代号时，根据公称尺寸、公差等级和基本偏差代号查表3-4并计算可得出极限偏差值。注意当孔的基本偏差在K、M、N和P～ZC时，孔的基本偏差上极限偏差ES要加上一个Δ值，Δ值可在表3-4中“Δ值”栏处查得。 查表确定尺寸Φ30F7、Φ35H6、Φ50JS7、Φ72K8和Φ90R7的极限偏差。......
2023-06-26
轴的基本偏差特点及极限偏差的应用与确定
【摘要】：从k～zc的基本偏差为下极限偏差ei，其值为正值，且k～zc基本偏差的绝对值依次增大。公称尺寸≤1000mm轴的基本偏差数值见表3-5。其使用方法是：当图样上给出的是公差带代号时，根据公称尺寸、公差等级和基本偏差代号查表3-5并计算可得出极限偏差值。 查表确定尺寸Φ35j6、Φ30h7、Φ50js7和Φ70f8的极限偏差。上述两例在实际工作中可以通过直接查表的方法获取极限偏差。
由图3-13可见，轴的基本偏差系列中，a～h基本偏差为上极限偏差es，其值为负值，且a～h基本偏差的绝对值依次减小（即从下向上逐渐靠近零线，其中h的基本偏差是es＝0）；j和js对称或基本对称分布在零线两侧，因此，其基本偏差既可以是上极限偏差，也可以是下极限偏差。从k～zc的基本偏差为下极限偏差ei，其值为正值，且k～zc基本偏差的绝对值依次增大（即从下向上逐渐远离零线）。
公称尺寸≤1000mm轴的基本偏差数值见表3-5。其使用方法是：当图样上给出的是公差带代号时，根据公称尺寸、公差等级和基本偏差代号查表3-5并计算可得出极限偏差值。
表3-5 轴的基本偏差数值（摘自GB／T 1800.1—2009）（单位：μm）
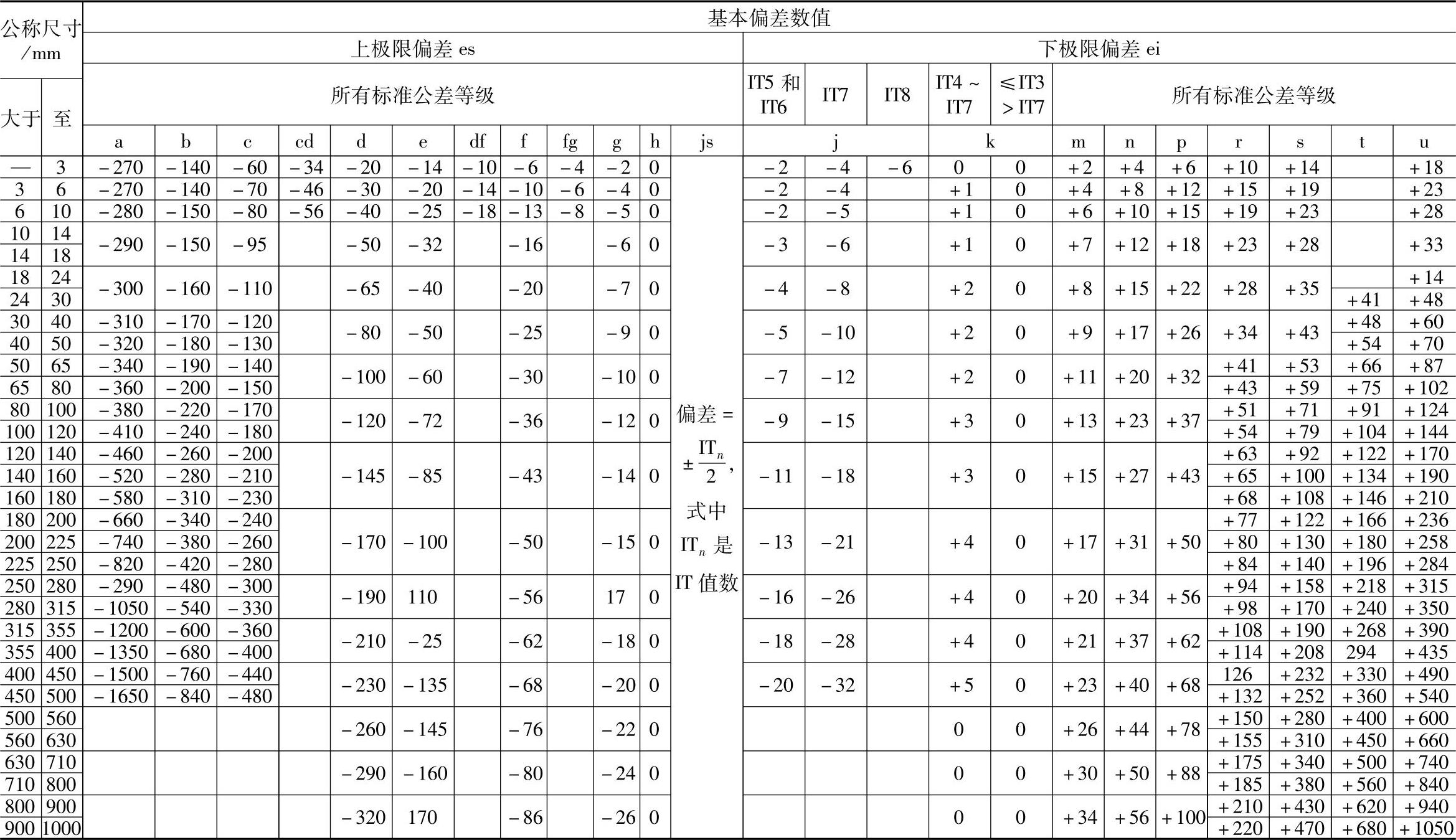
注：1.公称尺寸小于或等于1mm时，基本偏差a和b均不采用。2.公差带js7～js11，若ITn值数是奇数，则取偏差＝±
。
由表3-5可知：基本偏差a～h的上极限偏差可由表3-5查得，在这个范围内的下极限偏差则可通过查表3-1按式（3-6）计算求得，即ei＝es－IT，注意h的上极限偏差为零，其下极限偏差ei＝0－IT＝－IT；js的极限偏差为±IT／2；从j～zc的下极限偏差可由表3-5查得，在这个范围内的上极限偏差则可通过查表3-1按式（3-6）计算求得，即es＝ei＋IT。
【例3-5】 查表确定尺寸Φ35j6、Φ30h7、Φ50js7和Φ70f8的极限偏差。
解：1）Φ35j6，查表3-1得IT6＝0.016mm；查表3-5得基本偏差ei＝－0.005mm，则es＝ei＋IT6＝（－0.005＋0.016）mm＝＋0.011mm。由此可得Φ35j6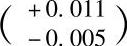
。
2）Φ30h7，查表3-1得IT7＝0.021mm；查表3-5得基本偏差es＝0mm，则ei＝es－IT7＝（0－0.021）mm＝－0.021mm。由此可得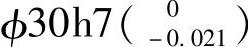
。
3）Φ50js7，查表3-1得IT7＝0.025mm；查表3-5得js的上极限偏差es＝＋（IT－1）／2＝［＋（25－1）／2］μm＝＋12μm＝＋0.012mm，而ei＝－（IT－1）／2＝［－（25－1）／2］μm＝－12μm＝－0.012（mm）。由此可得Φ50js7（±0.012）。
4）Φ70f8，查表3-1得IT8＝0.046mm；查表3-5得基本偏差es＝－0.030mm，则ei＝es－IT8＝（－0.030－0.046）mm＝－0.076mm。由此可得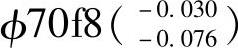
。
上述两例在实际工作中可以通过直接查表的方法获取极限偏差。
有关模具工基础知识问答的文章
- 详细阅读
-
基本偏差的概念与规定代号详细阅读
如图3-4所示，孔的基本偏差为下极限偏差，而轴的基本偏差为上极限偏差。基本偏差是确定公差带位置的参数，与公差等级无关。为了满足各种不同配合的需要，必须将孔和轴的公差带位置标准化。轴和孔的基本偏差代号各28个。必须指出，以轴为例，字母中除去与其他代号易混淆的五个字母i、l、o、q、w，增加了七个双字母代号cd、ef、fg、js、za、zb、zc。在基本偏差系列图中，表示了公称尺寸相同的28种孔和轴基本偏差相对零线的位置。......
2023-06-26
- 详细阅读
-
费用偏差和进度偏差分析及纠正措施详细阅读
对费用偏差和进度偏差的分析可以利用拟完工程计划费用、已完工程实际费用、已完工程计划费用三个参数完成，通过三个参数间的差额（或比值）测算相关费用偏差指标值，并进一步分析偏差产生的原因，从而采取措施纠正偏差。费用偏差分析方法既可以用于业主方的投资偏差分析，也可以用于施工承包单位的成本偏差分析。......
2023-09-25
-
认识公差与偏差的术语定义详细阅读
上极限偏差与下极限偏差统称为极限偏差。由于公差或偏差的数值比公称尺寸的数值小得多，在图中不便用同一比例表示，同时为了简化，在分析有关问题时，不画出孔、轴的结构，只画出放大的孔、轴公差区域和位置，采用这种表达方法的图形称为公差带图，如图2-4所示。通常零线位置表示公称尺寸，正偏差位于零线上方，负偏差位于零线的下方。......
2023-06-15
-
尺寸偏差与公差的区别与解析详细阅读
极限偏差是相对于公称尺寸偏离大小的数值，即确定了极限尺寸相对公称尺寸的位置，它是限制实际偏差的变动范围。而公差仅表示极限尺寸变动范围的一个数值。......
2023-06-26
-
尺寸公差和偏差的探讨详细阅读
图4-1 圆柱销2.公称尺寸(D，d)公称尺寸是设计给定的尺寸，用D和d表示。图4-3 公差与配合示意图5.尺寸偏差尺寸偏差简称偏差，是指某一尺寸减其公称尺寸所得的代数差，其值可正、可负或零。它是指公称尺寸所在的线，是偏差的起始线。......
2023-06-28
-
装配间隙与偏差控制详解详细阅读
装配间隙在坡口接头上称根部间隙，是焊前在接头根部之间预留的间隙，须通过装配来保证。因此，必须根据接头坡口准备的实际情况和焊接工艺条件在工艺规程中规定装配间隙的要求。也可以按表9-21提供的在一定板的厚度范围内给出根部间隙的名义尺寸，然后给出偏差值的要求。对于装配件的相互位置偏差，可以根据表9-22提出要求。......
2023-07-02
相关推荐