图5-57 管壳连接拉深排样图例5-4 图5-58所示为窄凸缘筒形件,材料为08F钢,料厚为0.5mm,年产量较大,经分析采用带料连续拉深冲压较为合理。......
2023-06-26
1.坯料形状和尺寸的确定
(1)形状相似性原则 拉深件的坯料形状一般与拉深件的截面轮廓形状近似相同,即当拉深件的截面轮廓是圆形、方形或矩形时,相应坯料的形状应分别为圆形、近似方形或近似矩形。另外,坯料周边应光滑过渡,以使拉深后得到等高侧壁(如果制件要求等高时)或等宽凸缘。
(2)表面积相等原则 对于不变薄拉深,虽然在拉深过程中板料的厚度有增厚也有变薄,但实践证明,拉深件的平均厚度与坯料厚度相差不大。由于拉深前后拉深件与坯料重量相等、体积不变,因此,可以按坯料面积等于拉深件表面积的原则确定坯料尺寸。
应该指出,用理论计算方法确定坯料尺寸不是绝对准确的,而是近似的,尤其是变形复杂的拉深件。实际生产中,由于材料性能、模具几何参数、润滑条件、拉深系数以及制件几何形状等多种因素的影响,有时拉深的实际结果与计算值有较大出入,因此,应根据具体情况予以修正。对于形状复杂的拉深件,通常是先做好简易的单工序试制模,并以理论计算方法初步确定的坯料进行反复试模修正,直至得到的制件符合要求时,再将符合实际的坯料形状和尺寸作为制造连续拉深模的依据。
在连续拉深中,无论是有凸缘的还是无凸缘的拉深件,均按有凸缘的拉深工艺计算。由于带料(条料)具有平面方向性,并受模具几何形状等因素的影响,制成的拉深件凸缘周边一般不整齐,尤其是深拉深件,因此在多数情况下还需采取加大带料(条料)中的工序件凸缘宽度的办法,拉深后再修边,以保证制件质量。经验值的修边余量可参考表4-29。
表4-29 连续拉深件的修边余量δ(一) (单位:mm)

注:表中的修边余量直接加在制件的凸缘上,再计算毛坯的展开尺寸。
带料连续拉深修边余量除了以上所列外,也可参考表4-30。
表4-30 连续拉深件的修边余量δ(二) (单位:mm)
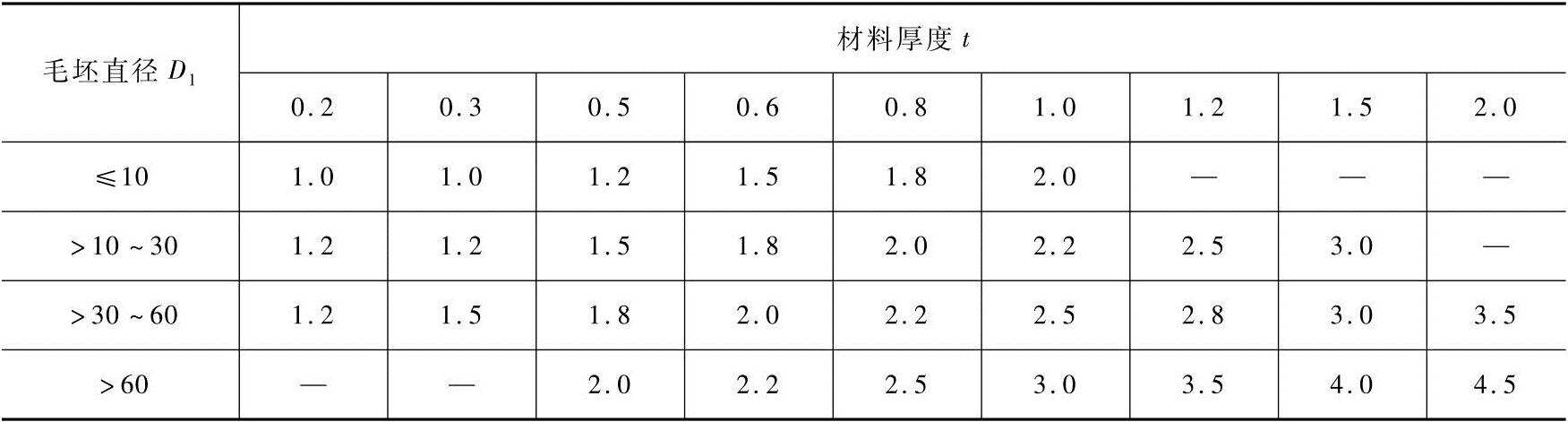
注:表中的修边余量加在制件毛坯的外形上,其毛坯计算公式为D=D1+δ。式中,D指包括修边余量的毛坯直径;D1为制件毛坯直径。
2.简单旋转体拉深件坯料尺寸的确定
旋转体拉深件坯料的形状是圆形,所以坯料尺寸的计算主要是确定坯料直径。对于简单旋转体拉深件,可首先将拉深件划分为若干个简单而又便于计算的几何体,并分别求出各简单几何体的表面积,再把各简单几何体的表面积相加即为拉深件的总表面积,然后根据表面积相等原则,即可求出坯料直径。
例如,图4-35所示的带凸缘筒形拉深件,将该制件分解成五个部分,分别按表4-31所列公式求出各部分的面积并相加,即得制件总面积为

毛坯面积A0为
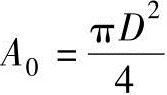
按等面积法A=A0
故毛坯直径按下式计算

式中 A———拉深件的表面积(mm2);
Ai———拉深件分解成简单几何形状的表面积(mm2)。
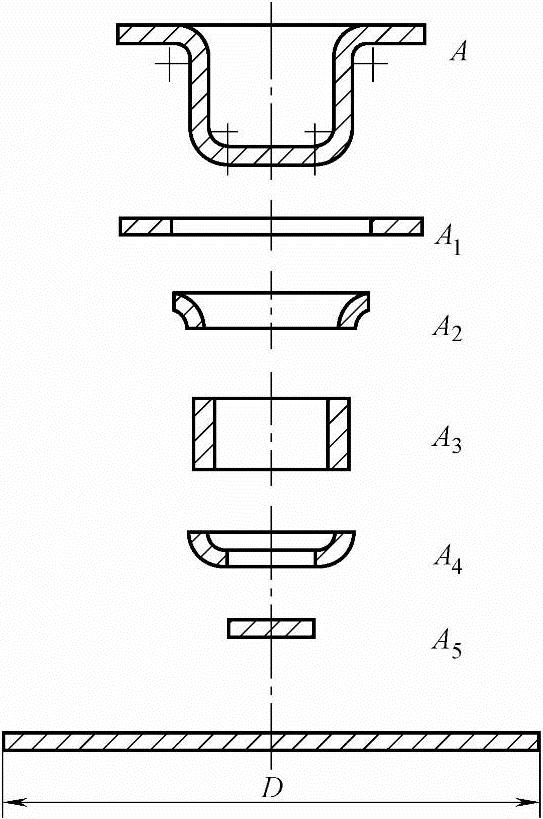
图4-35 带凸缘筒形件毛坯尺寸的计算
表4-31 简单几何形状的表面积计算公式
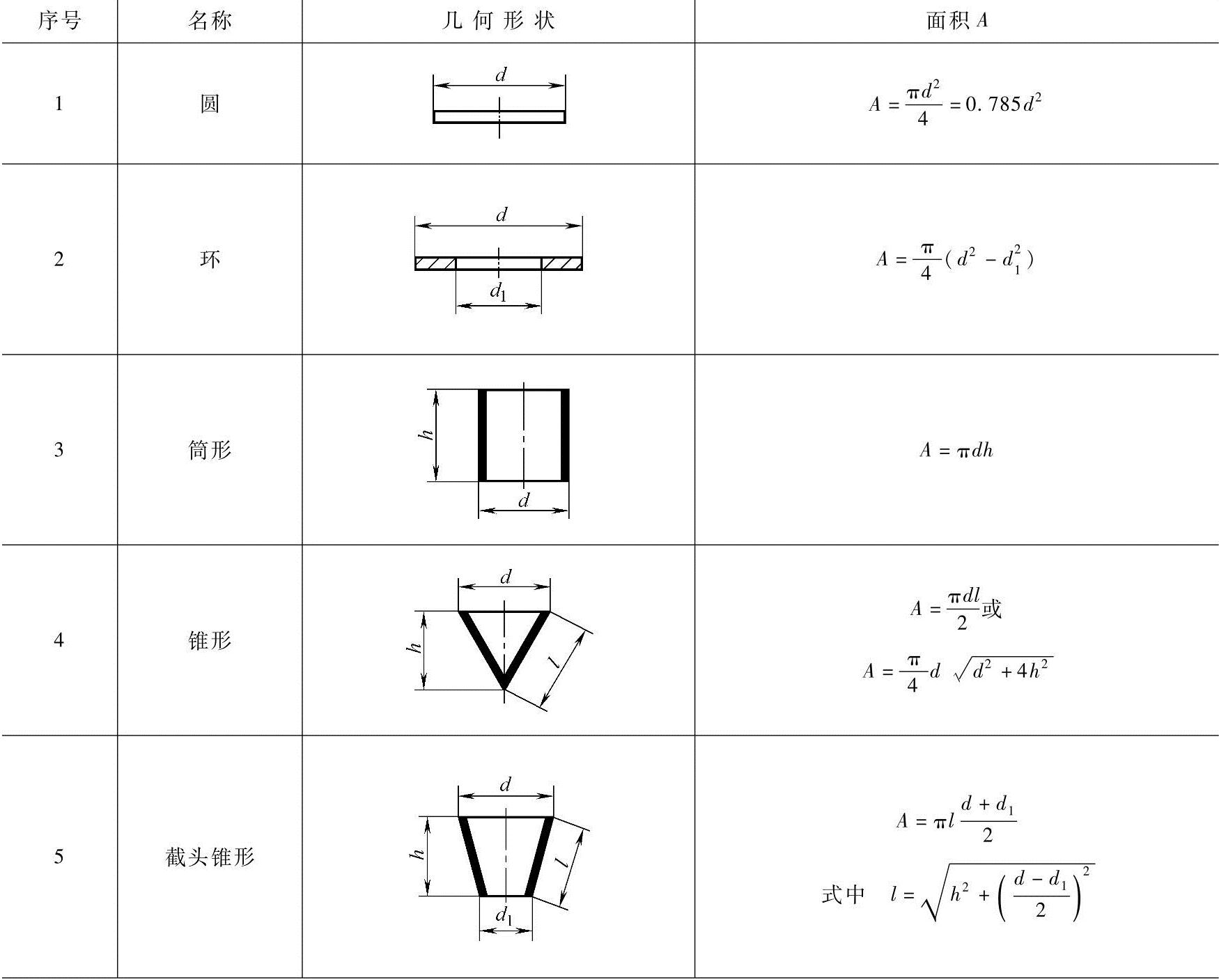
(续)

计算时,拉深件尺寸均按厚度中心线尺寸计算,但当带料(条料)厚度小于1.0mm时,也可以按制件图标注的外形或内形尺寸计算。
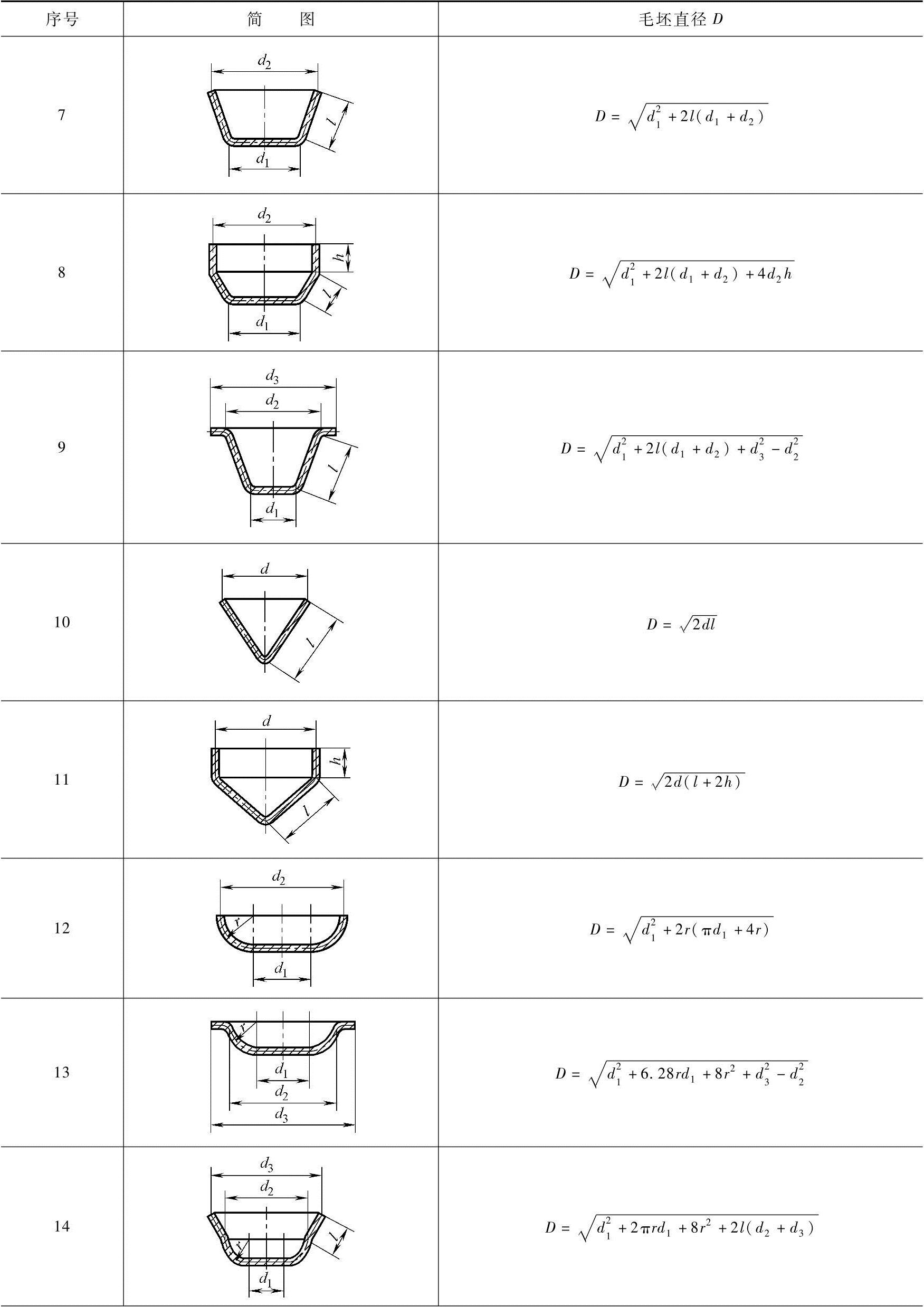
常用旋转体拉深件毛坯直径的计算公式见表4-32。
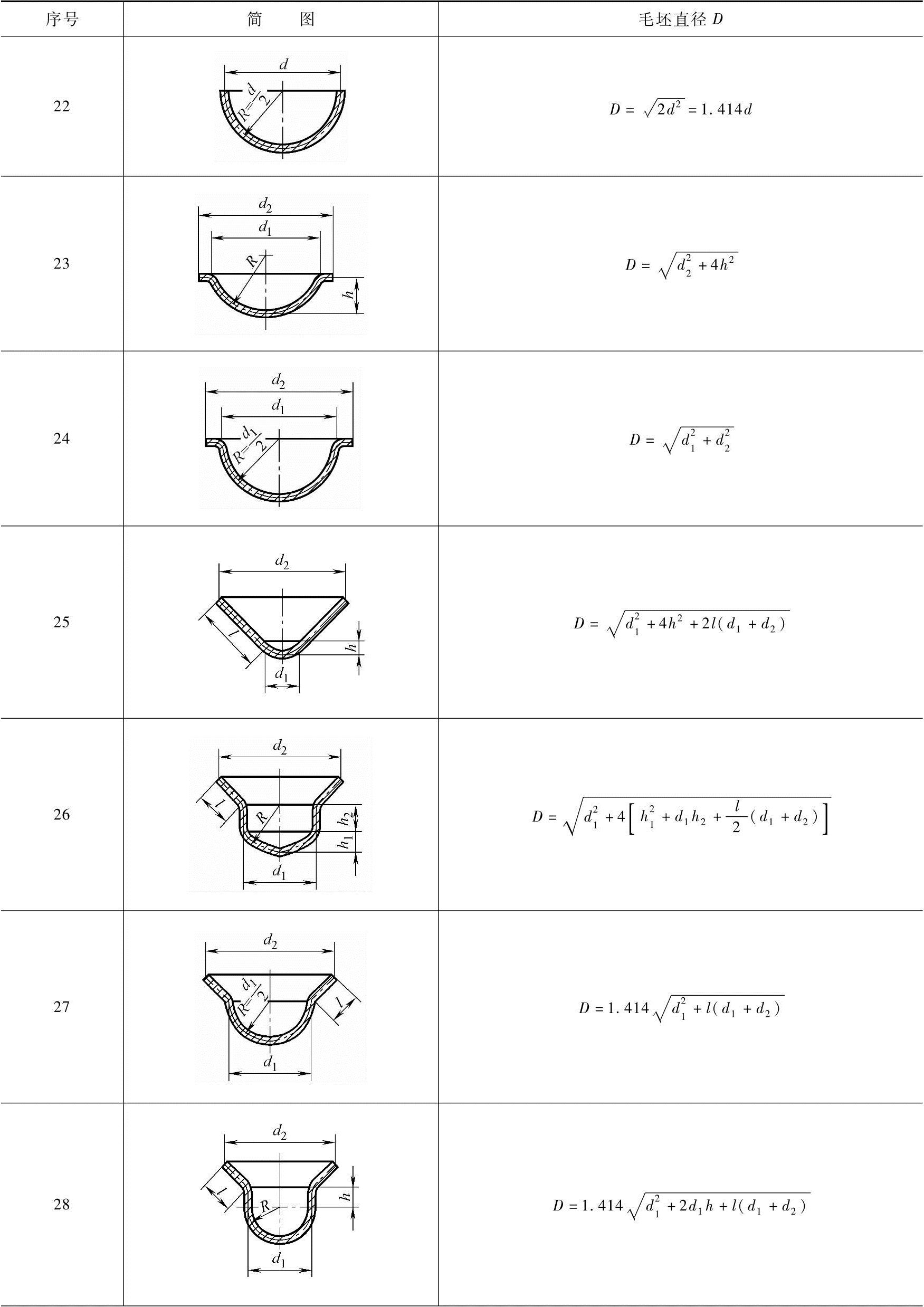
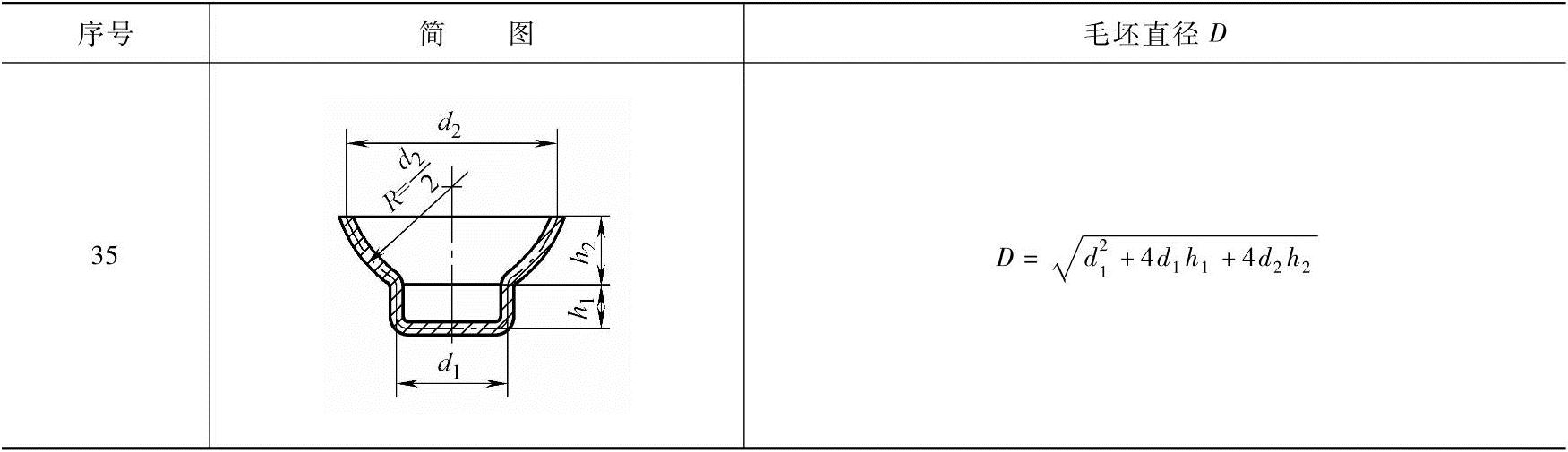
表4-32 常用旋转体拉深件毛坯直径的计算公式

(续)
(续)

(续)
(续)

(续)
有关多工位级进模设计实用手册的文章

图5-57 管壳连接拉深排样图例5-4 图5-58所示为窄凸缘筒形件,材料为08F钢,料厚为0.5mm,年产量较大,经分析采用带料连续拉深冲压较为合理。......
2023-06-26

无工艺切口的带料连续拉深时,材料变形的区域不与带料分开。图5-54 有工艺切口带料连续拉深带料在连续拉深时,是否要采用有工艺切口或无工艺切口,主要取决于拉深工艺,具体应用范围见表5-6。表5-6 带料连续拉深的应用范围(续)注:t—材料厚度;d—拉深件直径;h—拉深件高度;d凸—凸缘直径;D—包括修边余量的毛坯直径。......
2023-06-26

带料连续拉深排样设计应遵循以下几个步骤:1)计算出毛坯直径。3)确定连续拉深类型,主要确定带料是采用无工艺切口连续拉深,还是采用有工艺切口连续拉深,可以从表5-6查得。7)根据首次拉深直径d1计算出首次拉深凸、凹模圆角半径和高度h1,并核对h1/d1是否满足表4-35所列的数值,如果h1/d1小于表4-35所列的数值,d1就可以作为首次拉深的直径。......
2023-06-26

拉深系数用来表示拉深过程中的变形程度。合理地选定拉深系数可以使拉深次数减少到最小程度。表4-41 各种材料拉深系数极限值(推荐)2.拉深次数拉深次数通常是先进行概略计算,然后通过工艺计算来确定。为使各次拉深变形程度分配合理,确定拉深次数后,需将拉深系数进行合理化调整。......
2023-06-26

当直径减小时,可使其拉深高度增加,而当其圆角半径减小时,反而使其拉深高度减小。带料连续拉深每道工序的拉深高度,可根据如下相关公式计算。首次拉深假想毛坯直径:首次拉深高度:计算第二次至第n-1次拉深的高度 首次拉深进入凹模的面积增量x,在第二次拉深及以后的拉深中逐步返回到凸缘上。......
2023-06-26

材料及板厚:SUS304不锈钢,1.2mm。说明:1.工艺分析如图10-40a所示为不锈钢阶梯拉深、翻孔圆筒形件。该制件是一个带凸缘阶梯圆筒形拉深件,外形较小,尺寸精度要求高,特别是口部要求ф7.05±0.02mm,符合此要求必须增加一个整形工位才能达成。因制件材料为SUS304不锈钢,在计算拉深系数时,不锈钢的拉深系数要比普通材料的拉深系数略大些。......
2023-06-26

图5-27 冲切制件留载体3.留载体也留制件留载体也留制件这种方式常常用于满足后步工序的需要,带料(条料)上的制件虽经多工位级进模冲压结束了,但仍留在载体上,如小电流接线端子。......
2023-06-26

压边力的大小应允许在一定范围内调节。一般来说,随着拉深系数的减小,压边力许可调节范围减小,这对拉深工作是不利的,因为当压边力过大时,就会产生破裂,压边力过小时,会产生起皱,即拉深的工艺稳定性不好。相反,拉深系数较大时,压边力可调节范围增大,拉深工艺稳定性较好。表4-48 采用或不采用压边装置的条件为了更准确地估算是否需要压边装置,还应考虑拉深系数的大小。......
2023-06-26
相关推荐