预计出最大应变力的变形位置及变形形式，根据测试要求选定测试点。2）如果最大应力点的位置难以确定，或者为了了解截面应力分布规律和曲线轮廓段主应力过渡情况，可在截面上或者过渡段上比较均匀地布置5～7个测点。在已知主应力方向的情况下，应尽量保证贴片方向的一致性。......
2023-06-28
应力与应变的关系探析
【摘要】：图2-8 切应力和切应变的方向a）切应力方向 b）切应变方向由上述可知，应力状态与应变状态具有相似性。对于应力与应变的关系，不妨从方向和大小两方面进行叙述。首先讨论应力方向与应变方向之间的关系。对切应力和切应变，可用图2-8来表示。而对于正应力和正应变的方向，就不是这样简单了。
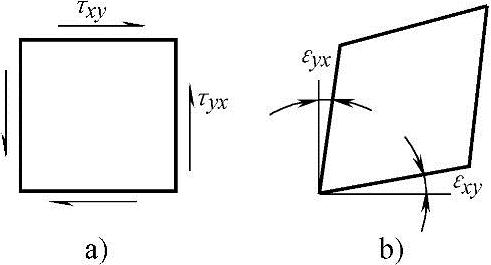
图2-8 切应力和切应变的方向
a）切应力方向 b）切应变方向
由上述可知，应力状态与应变状态具有相似性。对于小变形而言（不超过10-3～10-2数量级），两者的主坐标系是一致的。
对于应力与应变的关系，不妨从方向和大小两方面进行叙述。首先讨论应力方向与应变方向之间的关系。
对切应力和切应变，可用图2-8来表示。图2-8a的切应力方向对应于图2-8b的切应变方向，这很容易理解。而对于正应力和正应变的方向，就不是这样简单了。正应力为正值（受拉）时，正应变未必是正值（未必伸长）；正应力为负值（受压）时，正应变未必是负值（未必收缩）；正应力为零时，正应变未必为零（可能有伸长或收缩）。
为说明正应力和正应变方向的对应关系，也为说明应力分量与应变分量数值大小之间的关系，需要了解小变形时的应力与应变关系，它可叙述为：小变形时的应变分量正比于应力偏量，即
式中 λ———常数；
ε1、ε2、ε3———3个主应变值；
σ1′、σ2′、σ3′———3个主应力偏量值。
主应力偏量定义为：设σ1、σ2、σ3为3个主应力值，则平均应力σm=（σ1+σ2+σ3）/3，那么，3个主应力偏量分别为σ1′=σ1-σm，σ2′=σ2-σm，σ3′=σ1-σm。
由式（2-3），依照比例定律，又可导出以下公式：
式（2-3）、式（2-4）、式（2-5）也适用于全量应变理论的应力与应变关系。
有关多工位级进模设计实用手册的文章
- 详细阅读
-
上连杆应力应变分析优化详细阅读
上连杆在框架断路器操作机构的连杆结构中具有典型性，因此选择框架断路器上连杆为研究对象，使用ADAMS软件和ANSYS有限元软件计算机构运动过程中上连杆的应力应变，并比较ADAMS软件模态综合法和ANSYS有限单元法的计算结果。图3-8显示了ANSYS有限元软件有限单元方法计算出的t=0.0274s时刻，上连杆应力应变分布云图和3567号节点的应力应变时间历程曲线，可见上连杆的应力集中主要发生在内侧弯曲处，并与ADAMS软件刚柔耦合方法的计算结果吻合较好。......
2023-06-15
-
顺纹应力—应变关系及其工业化村镇建筑设计详细阅读
研究发现，重组竹顺纹受拉、顺纹受剪和垂直纹理方向受剪应力—应变关系呈直线型，应力—应变方程满足线弹性胡克定律。顺纹分段型应力—应变关系重组竹顺纹受压和垂直纹理平面纯剪应力—应变曲线在加载初期呈线性关系，当荷载超过比例极限后，曲线逐渐偏离原来的线性关系。试验数据统计分析表明，顺纹受压应力—应变曲线的非线性段可以采用二次曲线模拟。......
2023-10-12
-
动态应力应变的计算方法优化详细阅读
断路器操作机构的疲劳问题主要是由闭合与分断过程中的动态应力应变引起，因此对断路器操作机构疲劳寿命评估的前提是分合闸过程中零部件动态应力应变的准确计算。动态应力应变的计算基于柔性体的瞬态动力学分析，瞬态动力学分析是用于确定结构在承受任意随时间变化的载荷时的动力学响应的一种方法。常用的瞬态动力学求解方法包括：完全法、缩减法、模态叠加法，本章中柔性体应力应变的计算使用模态叠加法。......
2023-06-15
-
黏性土渗透变形与应力的关系详细阅读
在渗透变形试验的前期，渗透系数随水力梯度的增加变化幅度不大，基本保持不变。表5.6给出了渗透变形试验规程和本书建议的方法得到的临界水力梯度对比。由表5.6可知，含黏粗粒土试样即使在应力较低的情况下，其渗透变形的临界水力梯度也较“零附加应力”状态下的试件临界水力梯度高出许多。......
2023-06-28
-
拉深变形中毛坯的应力应变分析详细阅读
根据拉深过程中毛坯各部分的应力状况的不同，将其划分为五个部分。图4-34所示为圆筒形件在拉深过程中的应力与应变状态。以后σ1max又随着拉深的进行逐渐减小。综合以上分析可知，拉深时毛坯各区的应力、应变是不均匀的，且随着拉深的进行时刻在变化，拉深件的壁厚也是不均匀的。......
2023-06-26
-
模型验证及应力-应变曲线比较详细阅读
图8－32三种网格密度图网格一；网格二；网格三图8－33三种网格密度时的破坏路径网格一；网格二；网格三图8－34 所示为基于8.1.2 节中模型一计算和实验测量得到应力－应变曲线。计算结果与实测结果［23］吻合得较好。实验和计算的抗拉强度分别为11.43 MPa 和12.2 MPa。通过计算结果与实验结果的比较，验证了计算中采用的材料本构关系和参数。图8－34计算和实验得到的应力－应变曲线......
2023-06-27
-
结构力学：桁架多点应力应变测试及计算详细阅读
通过实验测试与理论计算结果的对比分析，验证“理想桁架”假设。根据理想桁架计算所得的内力是“主内力”，而由节点刚性等因素而引起的内力是“次内力”，在节点荷载作用下杆件内力以轴力为主，将节点简化为理想的铰接点是合理的。要求小组分工协作。考核报告质量、答辩及回答问题情况。......
2023-08-30
相关推荐