推力球轴承只能承受轴向载荷，单向推力球轴承只能承受一个方向的轴向载荷，双向推力球轴承可以承受两个方向的轴向载荷。单向推力球轴承可以限制轴和壳体的一个方向的轴向位移，双向轴承可以限制两个方向的轴向位移。如果安装条件许可，可以使用带球面座圈的单向或双向推力球轴承。......
2023-06-26
最小轴向载荷对14推力和推力角接触轴承的影响
【摘要】：接触角不等于零的角接触球轴承和滚子轴承，在运转中滚动体的自转轴线方向是经常变化的。如为钢制球：J0=4.2×10-8D5w图2-84表示推力向心滚子轴承作用于滚动体上的惯性力矩的方向。图2-86表示角接触球轴承中惯性力矩的方向。推力轴承和推力向心轴承中惯性力矩最大。表2-60 系数k值在多数情况下，推力轴承的实际载荷超过最小轴向载荷的计算值，此时轴承不需要预紧。对于推力球轴承，在某些情况下，无法克服由于惯性力矩引起的滑动。
牵连运动为圆周运动的物体，当其自转运动的轴线方向经常改变时，此物体受一惯性力矩，或称陀螺力矩的作用。
接触角不等于零的角接触球轴承和滚子轴承，在运转中滚动体的自转轴线方向是经常变化的。因此，在稳定运转状态下，滚动体中心受到离心力和惯性力矩的作用，其方向和数值可用下式表示：
Mk=J0ωwωcsinα （2-388）
式中 Mk——惯性力矩（N·m）；
J0——滚动体的转动惯量（g·mm·s2）；
ωw——滚动体自转角速度（1/s）；
ωc——滚动体公转角速度（1/s）；
α——轴承的接触角。
对于球轴承：
式中 γ——钢球材料的比重；
g——重力加速度；
Dw——钢球直径。
如为钢制球：
J0=4.2×10-8D5w
图2-84表示推力向心滚子轴承作用于滚动体上的惯性力矩的方向。图2-85表示推力球轴承中惯性力矩的方向。图2-86表示角接触球轴承中惯性力矩的方向。
由式（2-387）可知，惯性力矩MK与接触角的正弦成正比。由式（2-143）和式（2-146）可知，ωw和ωc都与轴承转速n成正比。因此接触角愈大、轴承转速愈高，则惯性力矩愈大。推力轴承和推力向心轴承中惯性力矩最大。当惯性力矩MK大于滚道对滚动体的摩擦力矩时就会发生回转滑动。
图2 - 84 推力向心滚子轴承中惯性力矩方向
图2 - 85 推力球轴承中惯性力矩的方向
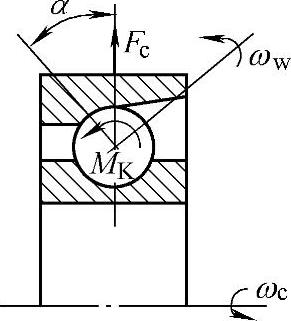
图2 - 86 向心推力球轴承中惯性力矩的方向
在推力球轴承中，轴圈如以转速n旋转，座圈静止不动，由式（2-146）可得
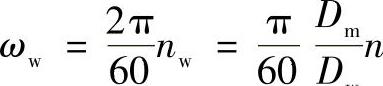
由式（2-143）可得
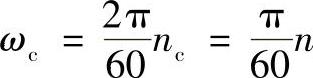
如将J0、ωw和ωc代入（2-387）式，则可得
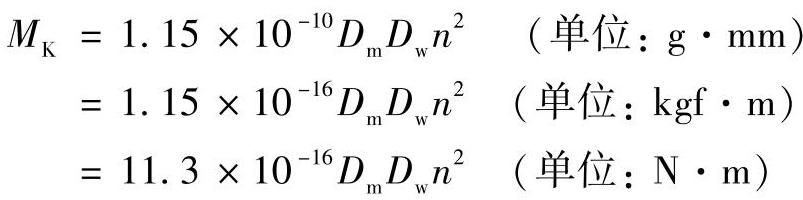
增大滚道对滚动体的摩擦力矩，可以防止由惯性力矩引起的回转滑动。不发生回转滑动的条件是：
MF﹥MK
MF是由轴向载荷引起的滚道对滚动体的摩擦力矩。各类推力和推力向心轴承中最小轴向载荷的计算公式列于表2-59中。
表2-59 最小轴向载荷Famin
表中 Famin——最小轴向载荷（N）；
Fr——径向载荷（N）；
α——接触角；
n——轴承转速（r/min）；
C0——额定静载荷（N）；
A——最小载荷常数，可由（2-390）式算出。
系数k的数值可由表2-60查出。
表2-60 系数k值
在多数情况下，推力轴承的实际载荷超过最小轴向载荷的计算值，此时轴承不需要预紧。但当实际轴向载荷小于最小载荷计算值时，轴承必须预紧。
对于推力球轴承，在某些情况下，无法克服由于惯性力矩引起的滑动。例如在双向推力球轴承中，有一列钢球通常是不受载的，此时，钢球和滚道之间必然产生滑动。使用经验表明，当推力球轴承在轻载荷下工作时，如实际轴向载荷小于0.000016C0时，只要有良好的润滑，则钢球与滚道之间由于惯性力矩产生的滑动，不致引起轴承损坏，在这种情况下，轴承可以不预紧。
有关滚动轴承应用手册的文章
- 详细阅读
-
双向推力轴承中的载荷分布优化探讨详细阅读
双向推力轴承在承受中心轴向载荷时，仅有一列滚动体承受载荷。这时可按单向推力轴承中的载荷分布计算滚动体载荷。双向推力轴承可以承受任意偏心载荷，如图2-31所示。表2-15 双向推力轴承的载荷分布积分JM、Ja当球轴承e≤0.3Dpw、滚子轴承e≤0.2619Dpw时，仅有一列滚动体承受载荷，在这种情况下，最大滚动体载荷可按表2-14计算。......
2023-06-26
-
角接触轴承载荷分布优化分析详细阅读
角接触球轴承和圆锥滚子轴承可以同时承受径向载荷和轴向载荷，如图2-23所示。但是单个角接触球轴承和圆锥滚子轴承不能单独承受纯径向载荷。图2 - 23 角接触球轴承图2 - 24 角接触轴承内圈载荷分布图此类轴承中的载荷分布与载荷角β有关。轴承中任一滚动体承受的载荷，由滚动体与滚道接触处的变形量来决定。表2-12 单列角接触轴承的载荷分布积分Jr、Ja 单列圆锥滚子轴承32315承受的径向载荷Fr=40kN，轴向载荷Fa=15kN，试计算轴承中最大滚动体载荷Qmax。......
2023-06-26
-
双列角接触轴承中的载荷分布分析详细阅读
对列角接触轴承可以承受任意方向的载荷，如图2-28所示。表2-13 双列轴承的载荷分布积分JrJa作用于轴承的载荷可有下列三种情况：1）Fa=0。这时轴承上仅有轴向载荷Fa，轴承中只有一列滚动体承受载荷，且此列各滚动体承受相同的载荷。这时轴承中两列承受载荷不同，Ⅰ列较大，Ⅱ列较小。如果Fa大于上述之值，则双列轴承完全像一个单列向心推力轴承那样起作用。......
2023-06-26
-
单向推力轴承载荷分布优化分析详细阅读
单向推力轴承可以承受偏心载荷，如图2-29所示。因此在这种情况下，各滚动体承受的载荷是不相同的。如引入载荷分布参数T，则那么式可改写为将式代入可得图2 - 29 单向推力轴承的载荷分布对球轴承：对滚子轴承：t=1.1由轴承受力平衡可得将式代入，并引入载荷分布积分Ja、JM可得式中由式和式可得在表2-14中列出了与JM、Ja的对应关系。因此单向推力球轴承仅能承受的偏心载荷。......
2023-06-26
-
如何正确装卸向心推力轴承详细阅读
并且支承的刚性好，没有轴承卡死的问题，因此应用比较广泛。此时轴承已稍带预过盈。采用两对角接触球轴承组成两个单向限位支承。每个支承中的两个轴承呈串联、两个单向限位支承呈背对背安装方式。在特定条件下，当两个轴承外圈的轴向位置不能改变时，可以用放置在内圈与轴肩之间的调整环来调整内圈的轴向位置，以期达到调整轴承游隙的目的。......
2023-06-26
-
调心滚子轴承与推力调心滚子轴承介绍详细阅读
调心滚子轴承能承受双向轴向载荷，同时也能承受较大的径向载荷。调心滚子轴承内圈有直孔的和锥孔的两种形式。带紧定套的调心滚子轴承，借助于锥孔和紧定套还可调整轴承的径向游隙。调心滚子轴承具有自动调心的功能，自动调整因安装条件不良造成的角度偏差的影响，调心滚子轴承对角度偏差的适应性能随轴承宽度系列、直径系列变化而变化。图1-34 振动筛用调心滚子轴承a）轴承内径d﹤75mm b）轴承内径d≥75mm图1-35 推力调心滚子轴承......
2023-06-26
-
推力轴承外形尺寸方案设计详细阅读
表1-92～表1-94列出了双向推力轴承不同直径系列及尺寸系列的外形尺寸。单向推力轴承外形尺寸延伸规则1）轴承轴圈内径d。2）轴承座圈外径D。表1-95 fD值算得的值：① 如和标准内已有外径尺寸接近，应优先按标准选取；② 如为新的外径尺寸，则按表1-96进行圆整。表1-97 fT值4）轴承最小单向倒角尺寸rsmin。rsmin按GB/T 274—2000表3选取，其数值原则上应接近但不应大于轴承高度T的7%和剖面宽度的7%的两值中较小值。......
2023-06-26
相关推荐