由上节所述可知，滚动轴承的额定动载荷是在假定的运转条件下确定的。在此假定载荷的作用下，轴承的寿命和实际载荷条件下的寿命相同，因此把此假定载荷称为当量动载荷，用P表示。式或式是滚动轴承当量动载荷计算的基本公式。图2-43和图2-44的曲线还可以表示为了得到相同的当量动载荷P，径向载荷Fr与轴向载荷Fa之间的关系。因此在确定这些类型轴承的当量动载荷P时，必须考虑接触角的变化。......
2023-06-26
双支承轴轴承载荷计算方法
【摘要】：多数情况下，可以把双支承轴的结构作为静定问题处理，利用力的平衡方程计算出支承反力，把得出的支承反力作为轴承载荷进行寿命计算。在大多数轴承应用场合下，把双支承轴作为静定问题，已能足够精确地确定轴承所承受的载荷。在这种支承结构中如果轴的刚性较大，仅考虑轴承的变形时，可用下述方法计算轴承载荷。由第2章第3节所述可知，各列承受的载荷大小与轴向载荷Fa和径向载荷Fr的相对数值有关。
1.静定解
一般机械中，大多为双支承轴。滚动轴承承受的载荷是由轴传递到轴承上的，也有的是由轴承座传递到轴承外圈上。多数情况下，可以把双支承轴的结构作为静定问题处理，利用力的平衡方程计算出支承反力，把得出的支承反力作为轴承载荷进行寿命计算。
非调心型滚动轴承可以承受一定的力矩，使内、外圈相对倾斜一定的角度。如果考虑力矩对轴变形的影响，则支承反力的数目将比力的平衡方程数多，故属静不定的问题。
在大多数轴承应用场合下，把双支承轴作为静定问题，已能足够精确地确定轴承所承受的载荷。在这种情况下，假定轴的变形对轴承载荷没有影响，将轴看作简支梁，轴承仅承受垂直于轴线的径向载荷。但是在高速机械、机床主轴等重要应用场合，必须把支承结构作为整体考虑以决定轴的挠度、轴的动载荷和轴承的受力情况。这时应把支承系统作为静不定系统求解。
表2-52中列出了几种典型载荷情况下，支承反力和简化计算公式。因为支承反力与作用于轴承上的载荷大小相等方向相反，所以所列公式可用来计算轴承载荷。表2-52中 FrⅠ——轴承Ⅰ的径向载荷（kN）；
FrⅡ——轴承Ⅱ的径向载荷（kN）；
FA——轴向载荷（kN）；
Ft——齿轮传动的圆周力（kN）；
Fs——齿轮传动的向心力（kN）；
d——齿轮的节圆直径（mm）；
r——齿轮的节圆半径（mm）。
轴向载荷由哪个轴承承受，应根据轴的支承结构形式决定。
2.静不定解
当考虑轴承的力矩反力时，因力的平衡方程数少于支承反力的数目，故属静不定问题。需加入轴的变形条件才能求出轴承载荷。
表2 - 52 两支承轴支承反力计算公式
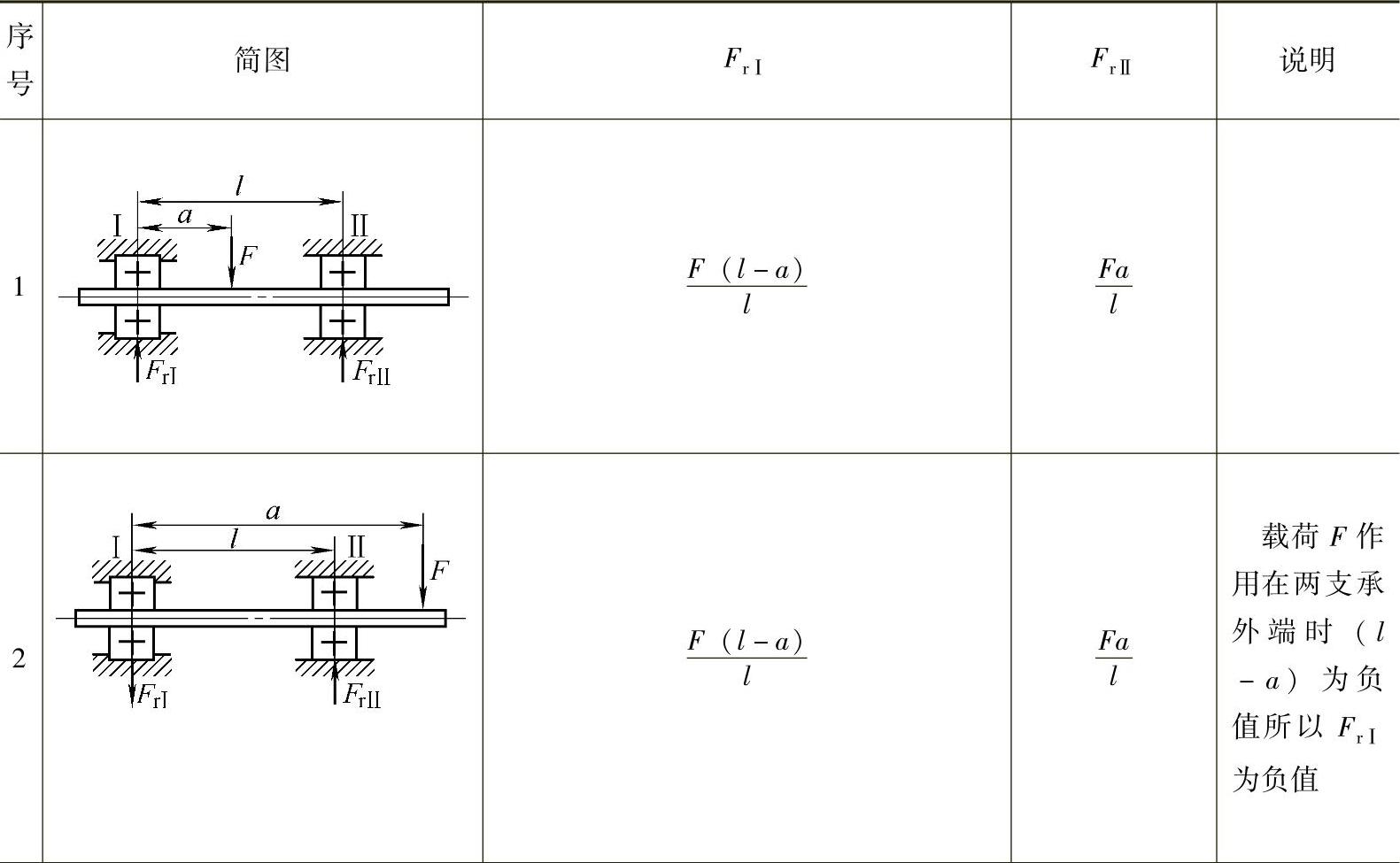
（续）
由材料力学关于梁的变形分析可得到轴的挠度y和转角θ与力矩M的关系为
EJy″=M（x） （2-347）
θ=y′ （2-348）
式中 
θ——轴的转角；
M（x）——作用于轴上的弯矩，弯矩符号的确定原则如图2-65所示；
E——轴材料的弹性模量；
J——轴的截面惯性矩。
图2-65 弯矩符号确定原则
对实心轴：
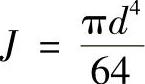
对空心轴：
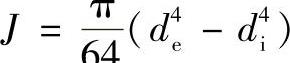
d为轴的直径，de、di分别为空心轴的外径和内径（mm）。
图2-66表示在两支承中间作用一集中力的一般情况。可以把支承分为两段来考虑。
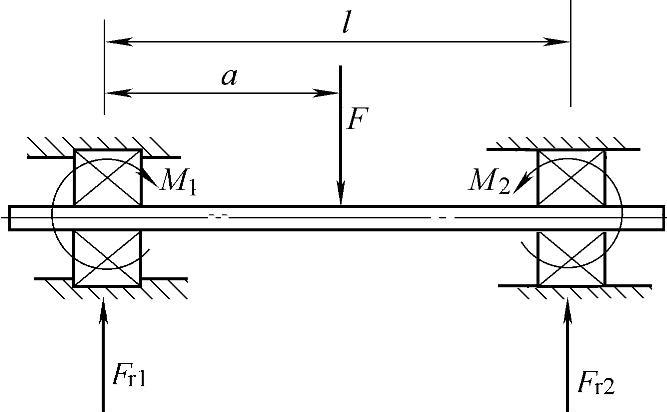
图2 - 66 两支承示意图
第一段：0≤x≤a
M（x）=Fr1x+M1
由式（2-347）可得
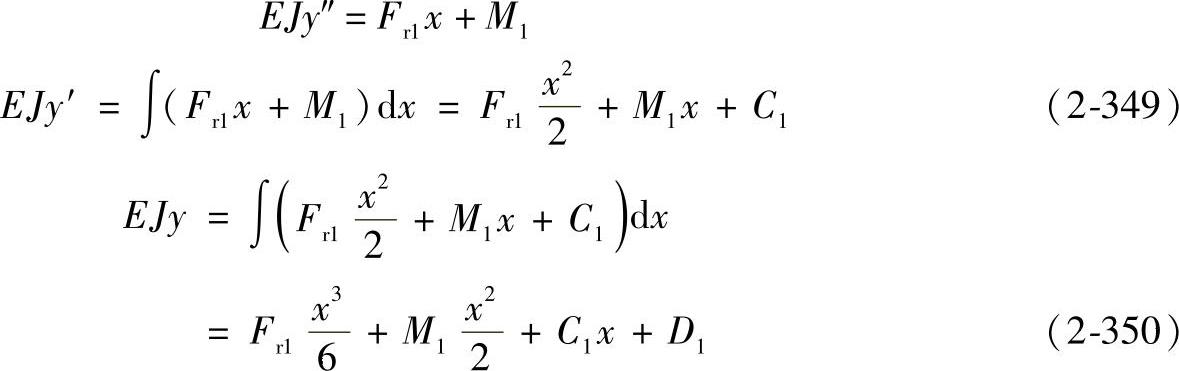
假定边界条件为
x=0 y′=θ1y=δr1
代入式（2-349）、式（2-350）中可得
C1=EJθ1
D1=EJδr1
则式（2-349）、式（2-350）可写为
第二段：
M（x）=Fr1x-F（x-a）+M1
由式（2-347）可得
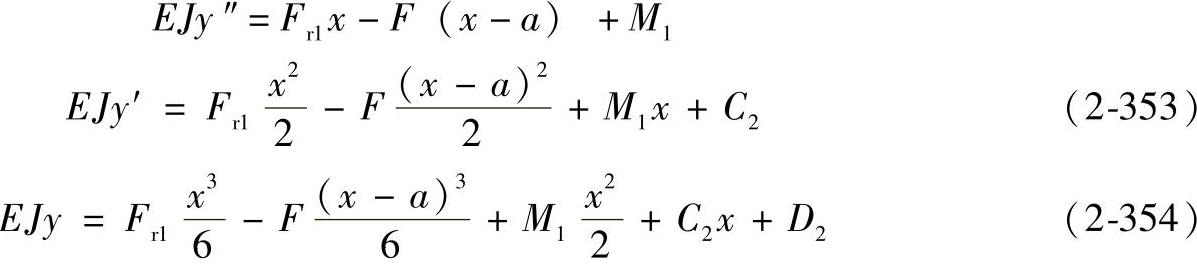
假定边界条件为
x=ly′=θ2y=δr2
代入式（2-353）、式（2-354）中可得
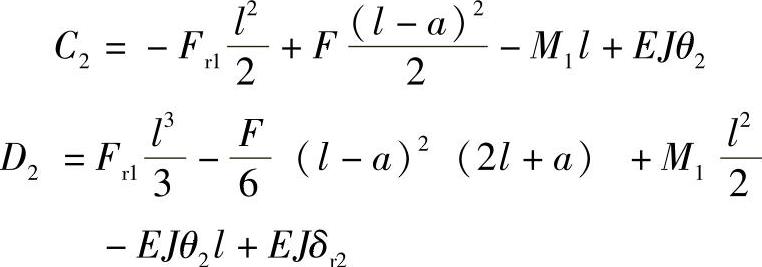
将C2、D2代入式（2-353）、（2-354）中可得
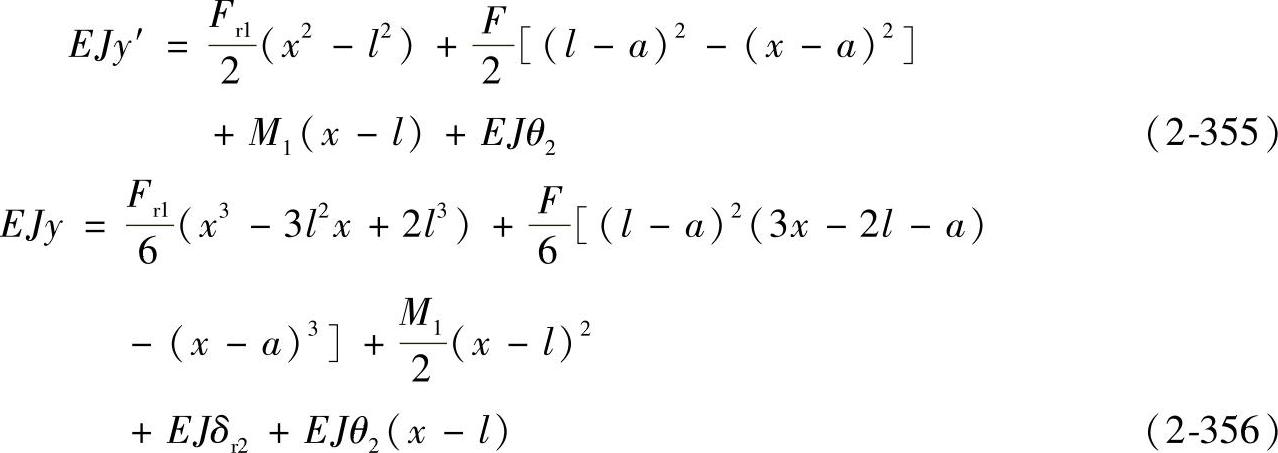
根据连续条件，在x=a时，由式（2-351）和式（2-352）计算出的y′值应相等；由式（2-352）和式（2-356）计算出的y值应相等，因而可得
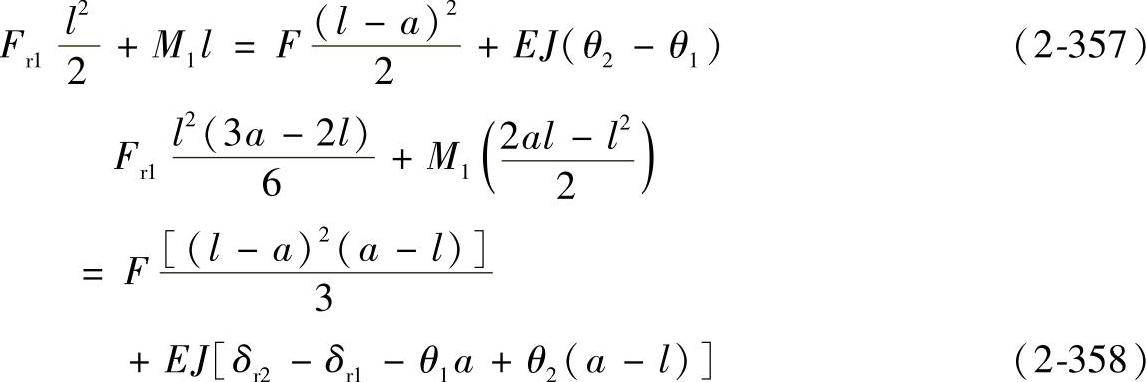
由式（2-357）和式（2-358）可得
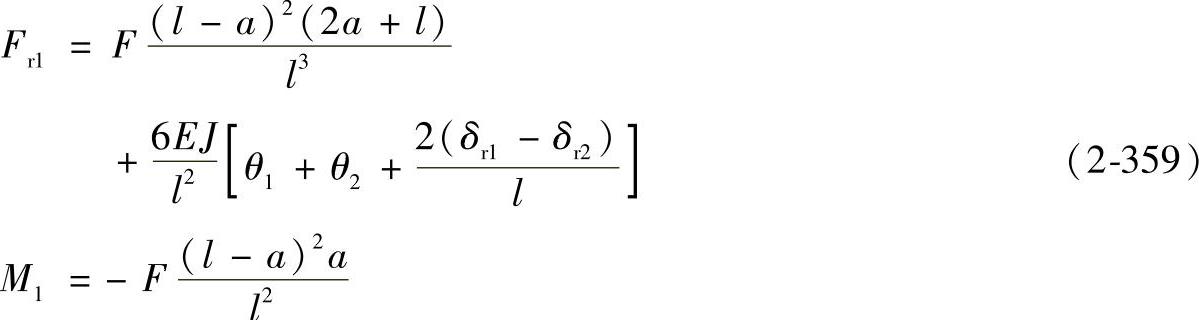
由力的平衡方程∑F=0、∑M=0可得
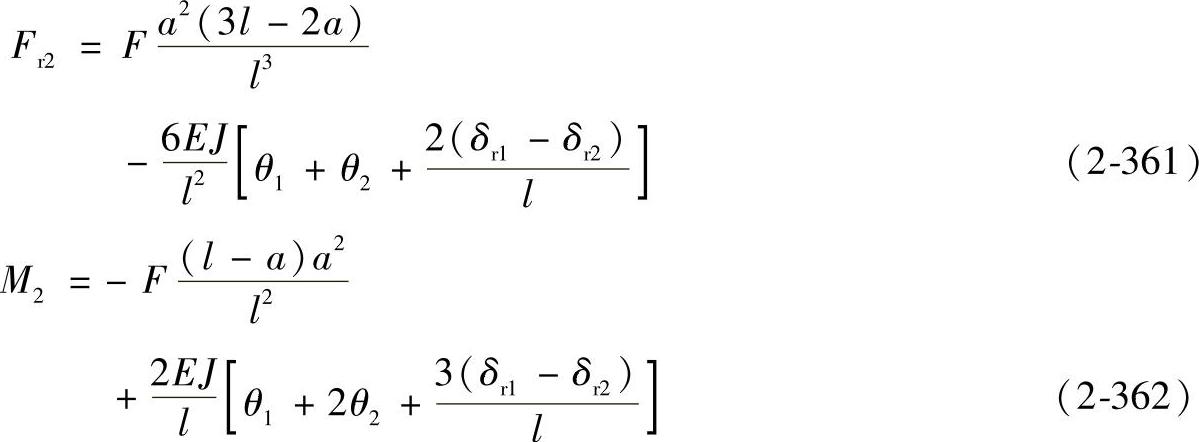
式（2-359）、式（2-360）是双支承轴考虑支承处力矩反力时的一般解，如作为静定问题处理时假定双支承轴承的径向变位相同和力矩反力为零，即
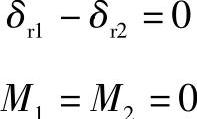
则将此条件代入式（2-359）～式（2-362）中可得
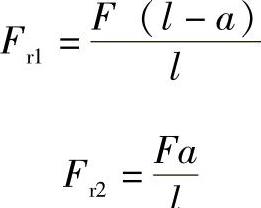
与表2-52中序号1的结果相同。10.3 三支承轴的轴承载荷计算
1.一般解法
由三个轴承支承的轴属静不定问题，如果轴的挠度较大，可利用轴的变形公式计算出轴承载荷。一般可将图3-67a的三支承轴简化为两个两支承轴，如图2-67b所示。然后按照上节所述的方法求解。
在图2-67中：
由式（2-359）～式（2-362）和式（2-363）、式（2-364）可得
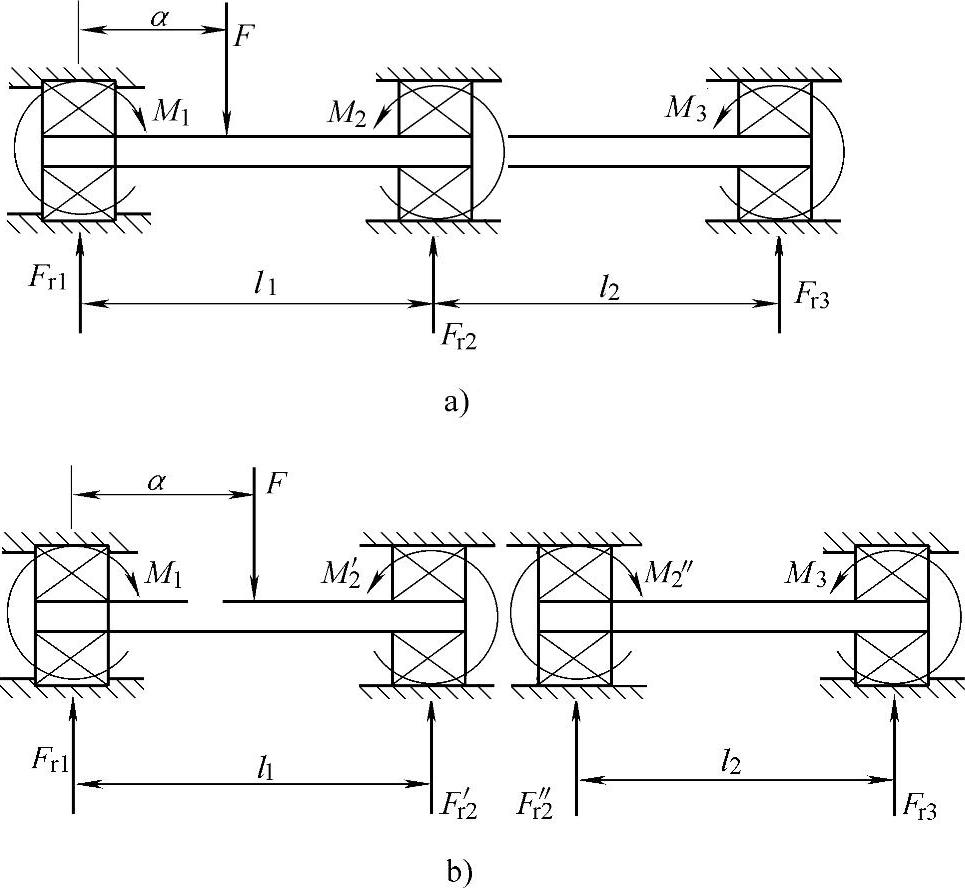
图2-67 三支承轴的简化方法
一般情况下，式（2-365）～式（2-370）中的θ1、θ2、θ3、δr1、δr2、δr3是很难确定的，因此解上述六个未知数相当繁杂。为简化计算，故作一些假定，可足够精确的确定出三支承轴中的轴承载荷。
2.简化解法
如果假定：1）各支承处轴承的力矩反力为零；
2）各轴承的径向变位之差甚小，可忽略不计；
3）轴的截面惯性矩相同；则可得δr1-δr2=0
δr2-δr3=0
M1=M2=M3=0 J1=J2
代入式（2-368）～式（2-370）可得
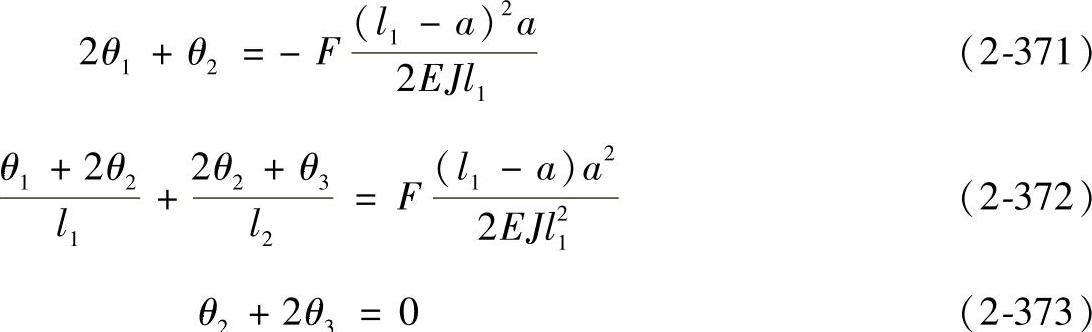
由式（2-371）～式（2-373）求出θ1、θ2、θ3，再代入式（2-365）～式（2-367）中可求得
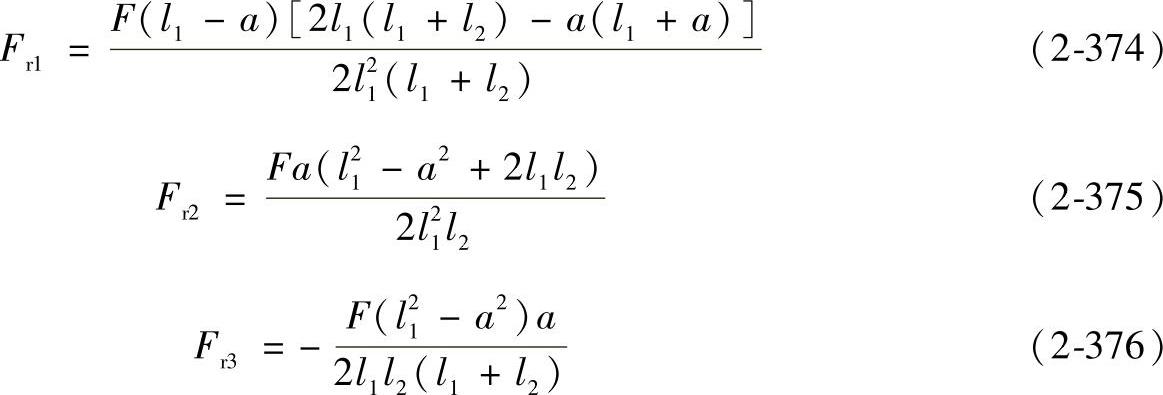
在上述假定的简化条件下，不同载荷条件时的轴承载荷计算公式列于表2-53中。
3.轴的变形甚小时的轴承载荷计算
当轴的刚性很大，其变形可忽略不计时，在载荷的作用下，轴的位置如图2-68所示。图中δr1、δr2、δr3分别表示轴承的径向位移。
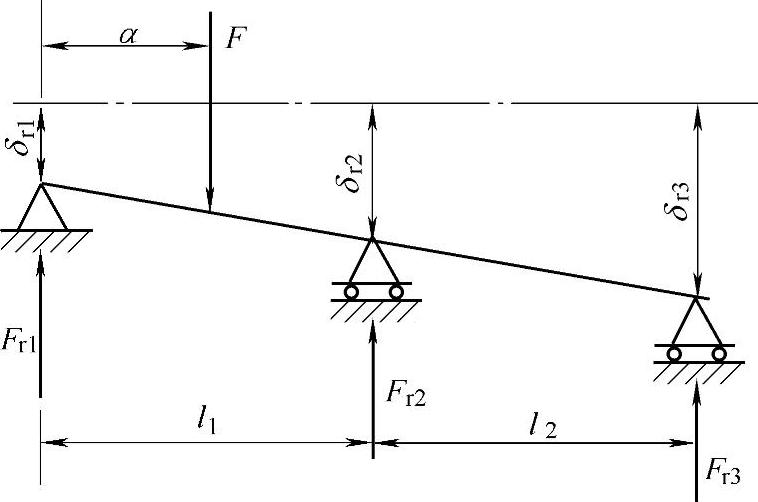
图2-68 轴承径向变位简图
表2 - 53 三支承轴的轴承负荷计算公式
（续）
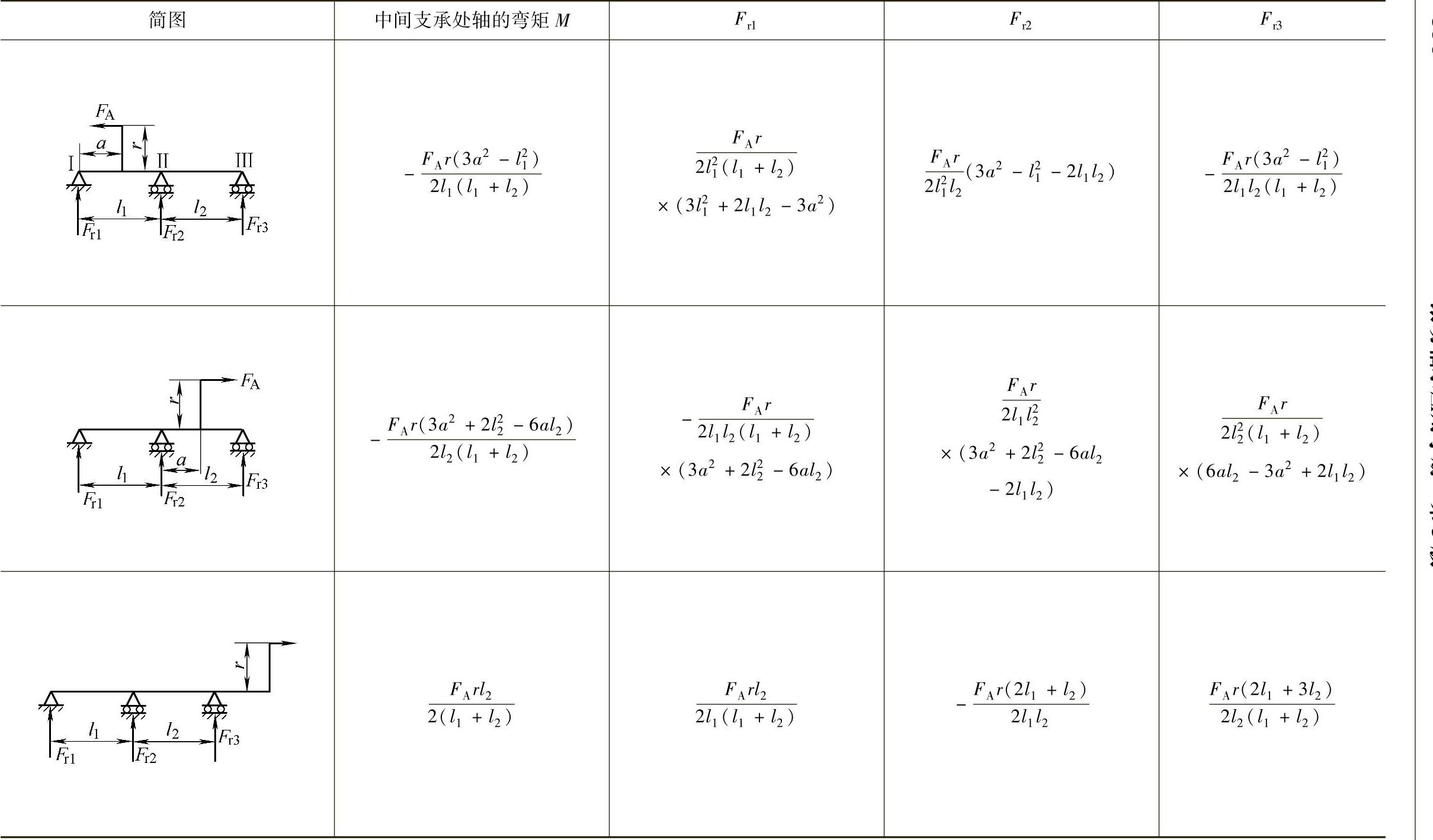
注：1.F与FA以图示方向为正，如与图示方向相反，应以（-F）和（-FA）代入。
2.Fr1、Fr2、Fr3以图示方向为正。
由本章关于轴承径向变位和载荷分布理论可得
δr1=K1′Fnr1 （2-377）
δr2=K2′Fnr2 （2-378）
δr3=K3′Fnr3 （2-379）
式中 对球轴承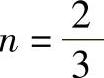
对滚子轴承n=0.9
由于轴的挠度可忽略不计，由图2-68的几何关系可得
将式（2-377）～式（2-379）代入可得
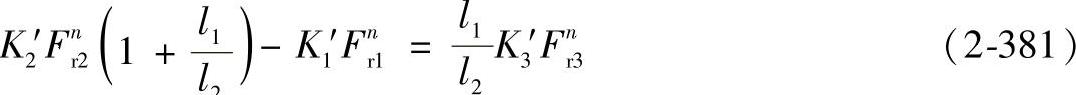
式中，K1′、K2′、K3′为轴承变形常数，可由第2章第2节求出。如果选用同一型号的轴承，则K1′=K2′=K3′，这时式（2-381）可写为
由此变形条件和力的平衡方程即可求出Fr1、Fr2、Fr3的数值。
4.图2-69所示支承结构的轴承载荷计算
图2-69所示为一支承处同时安装两个相同型号的向心推力轴承，另一支承处安装一个仅能承受径向载荷的向心轴承。在这种支承结构中如果轴的刚性较大，仅考虑轴承的变形时，可用下述方法计算轴承载荷。
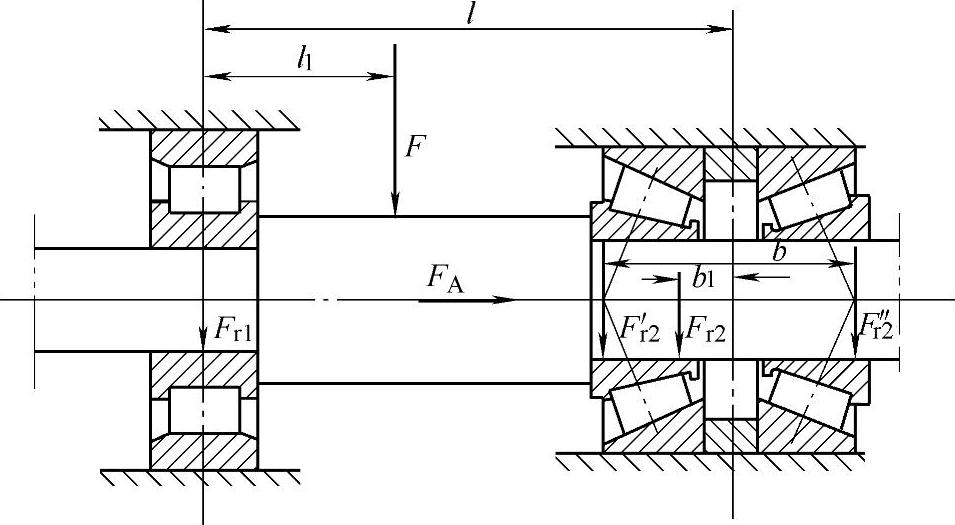
图2-69 支承结构简图
两个相同型号的向心推力轴承，背对背或面对面安装时，可以看作是一个对称的双列向心推力轴承。由第2章第3节所述可知，各列承受的载荷大小与轴向载荷Fa和径向载荷Fr的相对数值有关。
图2-69中 Fr′2——左侧向心推力轴承承受的径向载荷；
Fr″2——右侧向心推力轴承承受的径向载荷；
Fr2——Fr′2与Fr″2的合力。是作用在双列向心推力轴承上的合成径向载荷；
b——两个向心推力轴承载荷作用中心之间的距离；
b1——Fr2的作用点距两轴承几何中心的距离；
FA——外加轴向载荷，因为左端支承不能承受轴向载荷，故为作用于双列向心推力轴承上的轴向载荷；
F——外加径向载荷。
由图示关系可得
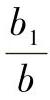的数值可由第2章第3节所述双列向心推力轴承载荷分布理论求出，现列于表2-54和图2-70中。
利用图2-70或表2-54决定轴承载荷的步骤为：
表2-54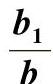
与
的关系
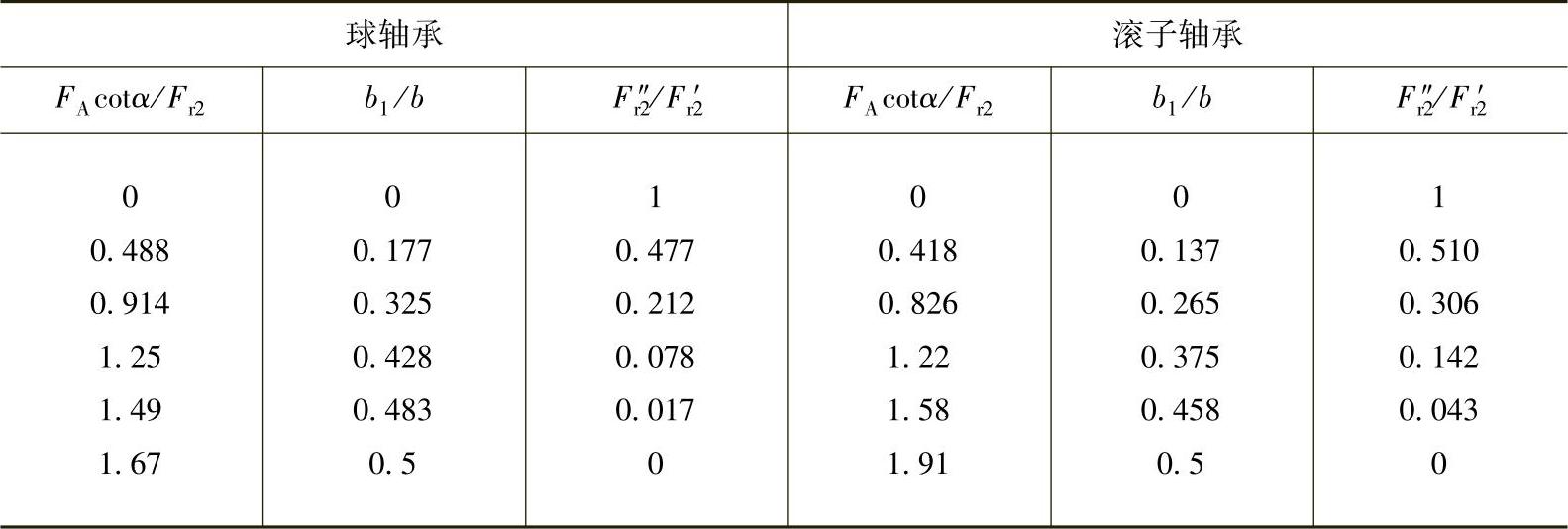
1）假定合力Fr2作用在两个向心推力轴承的几何中心，即b1（1）=0计算出第一次近似值F（1）r2。
2）计算下列数值：
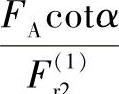
其中α为向心推力轴承的接触角。
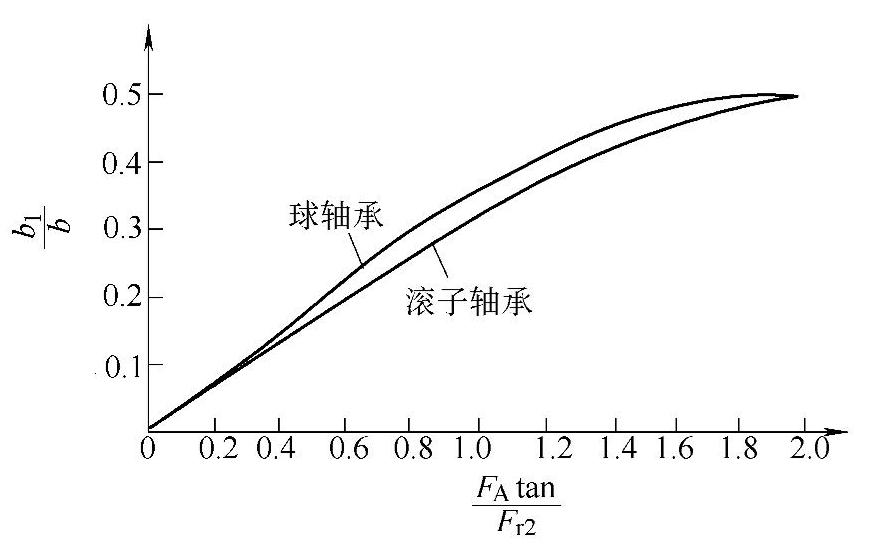
图2-70
与
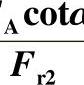关系图
对向心推力球轴承：
对圆锥滚子轴承：
cotα=2.5Ye和Y的数值都可由滚动轴承样本中查出。
3）在图2-70中查出与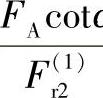
相对应的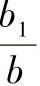
的第二次近似数值。
4）根据受力情况选取适当的b1（2）值，作为Fr2的作用点，计算出Fr2的第二次近似值F（2）r2。
经过几次逼近计算即可足够精确地确定Fr2的数值。
相对安装的两个相同型号的向心推力轴承，可按双列向心推力轴承进行寿命计算；这时其额定动载荷和当量动载荷都应取双列轴承的数值。如已知单列轴承的额定动载荷为C1，则双列轴承的额定动载荷为：
对向心推力球轴承 C=1.62CⅠ
对圆锥滚子轴承 C=17.71CⅠ
有关滚动轴承应用手册的文章
- 详细阅读
-
如何计算滚动轴承的载荷传递——滚动体载荷详细阅读
滚动轴承承受的载荷是通过滚动体由一个套圈传向另一个套圈的。即αi=αe由作用于滚动体上载荷的平衡可知，外圈对滚动体作用的载荷Qe与内圈对滚动体的载荷Qi数值相等，方向相反。所以由式（2-1）可得 7307B角接触轴承承受纯轴向载荷Fa=1kN，求作用于每个钢球上的滚动体载荷是多少？图2-4 圆锥滚子轴承的滚动体负荷外圈作用于滚动体上的载荷为内圈作用于滚动体上的载荷分为两部分。......
2023-06-26
-
轴和轴承：用途和分类详细阅读
(一)轴的用途及分类轴是组成机器的主要零件之一。在高速、高精度、重载、结构上要求剖分等场合下，滑动轴承就显示出它的优异性能，对于在低速但有冲击的条件下工作的机器，也采用滑动轴承。图3-14所示为一整体式滑动轴承，它由轴承座和整体轴瓦等组成。轴承合金又称巴氏合金。铅锑轴承合金的各种性能与锡锑轴承合金接近，但这种材料较脆，不宜承受较大的冲击载荷，一般用于中速、中载的轴承。......
2023-06-16
-
如何选用适合额定静载荷的轴承？详细阅读
对于低速旋转或缓慢摆动的轴承，应按额定静载荷和接触疲劳寿命两种方法分别计算，选取尺寸较大的轴承。在按额定静载荷选用轴承时，还应注意与轴承相配合部件的刚性。表1-17 允许静载荷系数fs由式求出C0值，查附录和轴承样本，即可确定应选用的轴承代号。如果硬度低于上述范围，则可用上述公式近似确定轴承的额定动载荷和额定静载荷。......
2023-06-26
-
双列角接触轴承中的载荷分布分析详细阅读
对列角接触轴承可以承受任意方向的载荷，如图2-28所示。表2-13 双列轴承的载荷分布积分JrJa作用于轴承的载荷可有下列三种情况：1）Fa=0。这时轴承上仅有轴向载荷Fa，轴承中只有一列滚动体承受载荷，且此列各滚动体承受相同的载荷。这时轴承中两列承受载荷不同，Ⅰ列较大，Ⅱ列较小。如果Fa大于上述之值，则双列轴承完全像一个单列向心推力轴承那样起作用。......
2023-06-26
-
向心轴承载荷分布特性分析详细阅读
向心轴承在承受径向载荷Fr后，上半圈的滚动体不承受载荷，下半圈的滚动体承受载荷。图2 - 19 向心轴承中的弹性变形图2 - 20 向心轴承中的径向变位在图2-19中：ψ——各滚动体中心与最大载荷滚动体之间的夹角，ψ0=0°，，ψ2’,…对球轴承：对滚子轴承 t=1.1图2-21为轴承载荷分布图。每个滚动体载荷可以分解为两个分量，由力的平衡可得将式代入可得由上式可看出，Qmax与作用于轴承上的载荷Fr和滚动体数量z有关。......
2023-06-26
-
角接触轴承载荷分布优化分析详细阅读
角接触球轴承和圆锥滚子轴承可以同时承受径向载荷和轴向载荷，如图2-23所示。但是单个角接触球轴承和圆锥滚子轴承不能单独承受纯径向载荷。图2 - 23 角接触球轴承图2 - 24 角接触轴承内圈载荷分布图此类轴承中的载荷分布与载荷角β有关。轴承中任一滚动体承受的载荷，由滚动体与滚道接触处的变形量来决定。表2-12 单列角接触轴承的载荷分布积分Jr、Ja 单列圆锥滚子轴承32315承受的径向载荷Fr=40kN，轴向载荷Fa=15kN，试计算轴承中最大滚动体载荷Qmax。......
2023-06-26
-
滚动轴承的当量静载荷优化详细阅读
如果轴承的实际载荷条件与确定额定静载荷的假定条件不同，则应将实际载荷换算为当量静载荷后才能与额定静载荷相比较。图中的曲线表示，为了得到相同的当量静载荷P0的Fr与Fa相对关系。用角注Ⅰ、Ⅱ表示轴承中的两列，并且假定Ⅰ列承受较重的载荷，即假定Ⅰ列的塑性变形量较大，因此只用QmaxⅠ来计算轴承的当量静载荷。......
2023-06-26
相关推荐