首页理论教育传动对滚动轴承载荷计算的影响

传动对滚动轴承载荷计算的影响

2023-06-26 理论教育版权反馈

【摘要】：轴承所承受的载荷，主要与各类传动中的作用力有关。从动轮的轴向力方向与主动齿轮相反。图2-58 直齿圆锥齿轮传动图2-59 斜齿圆锥齿轮传动在计算斜齿圆锥齿轮传动的向心力Fs和轴向力FA时必须首先规定如何确定螺旋角的方向及齿轮的旋转方向。因此带作用于轴上的向心力Fs与初拉力、包角和转速有关。

轴承所承受的载荷，主要与各类传动中的作用力有关。为方便读者使用，今将常用的齿轮传动和皮带传动的作用力公式列举如下：

1.直齿圆柱齿轮

图2-56为直齿圆柱齿轮传动示意图。图中齿轮Ⅰ为主动轮，用角注1表示；齿轮Ⅱ为从动轮，用角注2表示（其他类型齿轮亦同）。

圆周力：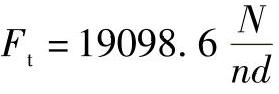

向心力：F_s=F_t·tanα

式中 N——传动功率（kW）；

n——齿轮转速（r/min）；

d——齿轮节圆直径（mm）；

α——齿轮节圆压力角（°）。

图2-56 直齿圆柱齿轮传动

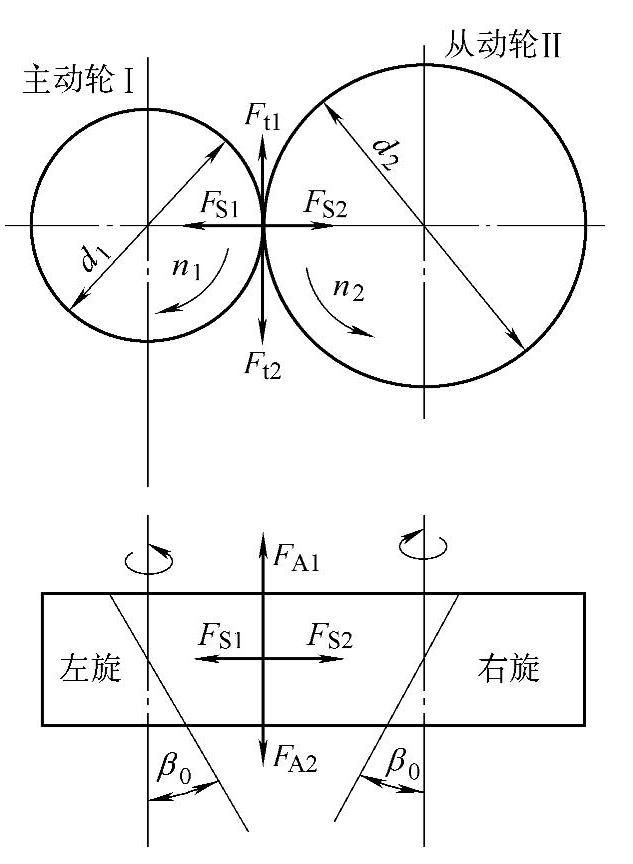
图2-57 斜齿圆柱齿轮传动

2.斜齿圆柱齿轮传动

图2-57为斜齿圆柱齿轮传动示意图。传动载荷计算公式如下：

圆周力：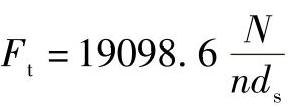

向心力：

轴向力：F_A=F_ttanβ

变位斜齿圆柱齿轮的端面节圆直径与端面分度圆直径的关系为

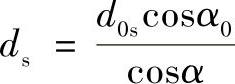
式中 d_s——齿轮端面节圆直径（mm）；

d_0s——齿轮端面分度圆直径（mm）；

α₀——齿轮的端面压力角；

α——齿轮的端面啮合角；

α_n——齿轮的法面啮合角；

β——齿轮分度圆上的螺旋角；

N——传动功率（kW）；

n——转速（r/min）。

斜齿圆柱齿轮轴向力方向的确定原则：

1）主动齿轮为右旋齿时，以右手四指的方向表示主动齿轮的旋转方向，则大姆指所指的方向即为主动齿轮所受轴向力的方向。

2）主动齿轮为左旋齿时，以左手同上法确定方向。从动轮的轴向力方向与主动齿轮相反。

3.直齿圆锥齿轮传动（直齿锥齿轮）

直齿圆锥齿轮传动的作用力如图2-58所示。

圆周力：F_t=19098.

向心力：F_s1=F_t1tanα₀cosδ₁=-F_A2

轴向力：

F_A1=F_t1tanα₀sinδ₁=-Fs2

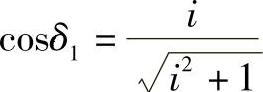
因为直齿圆锥齿轮传动中，两个齿轮的轴线夹角一般为90°，所以主动齿轮的轴向力与从动齿轮的向心力数值相等方向相反，主动齿轮的向心力与从动齿轮的轴向力数值相等方向相反。

式中 δ₁——小齿轮的半节锥角；

i——传动比；

α₀——齿轮标准压力角；

d_m——直齿圆锥齿轮的平均

节圆直径（mm）。

4.斜齿圆锥齿轮（螺旋锥齿轮）传动

斜齿圆锥齿轮传动的作用力如图2-59所示。圆周力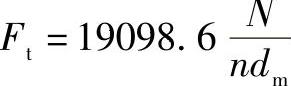：向心力和轴向力的计算公式列于表2-50中。

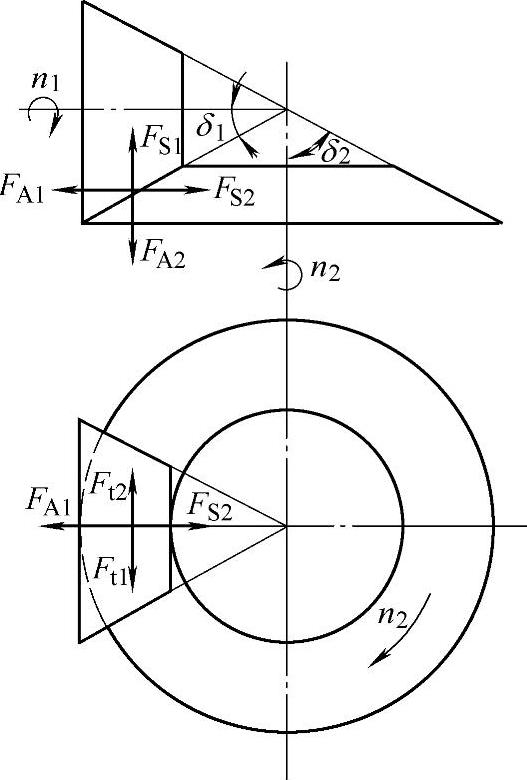
图2-58 直齿圆锥齿轮传动

图2-59 斜齿圆锥齿轮传动

在计算斜齿圆锥齿轮传动的向心力F_s和轴向力F_A时必须首先规定如何确定螺旋角的方向及齿轮的旋转方向。

确定螺旋角左旋或右旋的方法如图2-60所示。对着齿轮小端面看，如齿长曲线顺时针方向离开中心者为右旋，逆时针方向离开中心者为左旋。

确定齿轮旋转方向的方法如图2-61所示，对着齿轮大端面看，是顺时针旋转还是逆时针旋转。

由表2-50所列公式计算出的轴向力F_A为正时，表示轴向力的方向是由圆锥顶点指向齿轮大端，即离开圆锥顶点的方向。如F_A为负值，表示轴向力指向圆锥顶点，如图2-62所示。

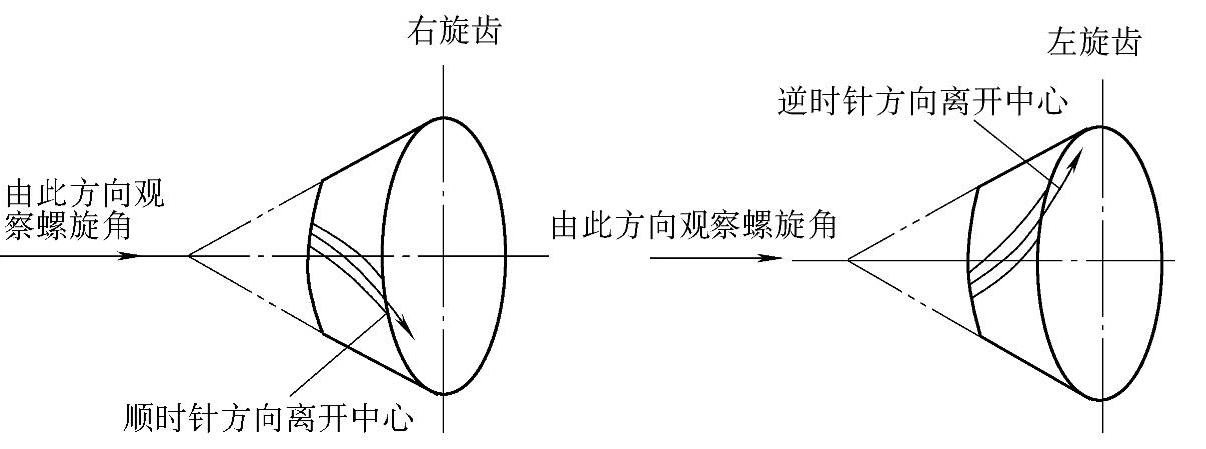
图2-60 确定螺旋角左旋或右旋的原则

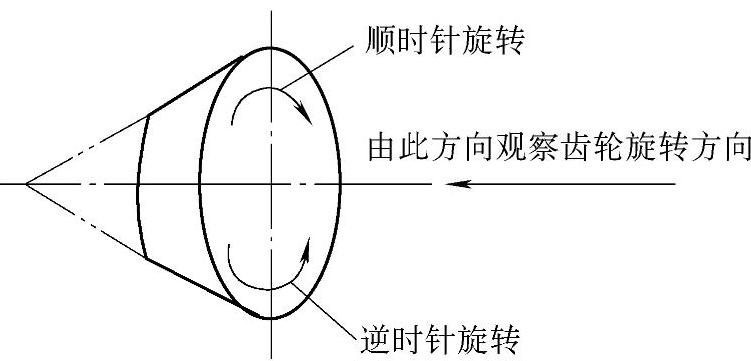
图2-61 齿轮旋转方向的确定原则

表2-50 斜齿圆锥齿轮传动的向心力F_S，轴向力F_A的计算公式

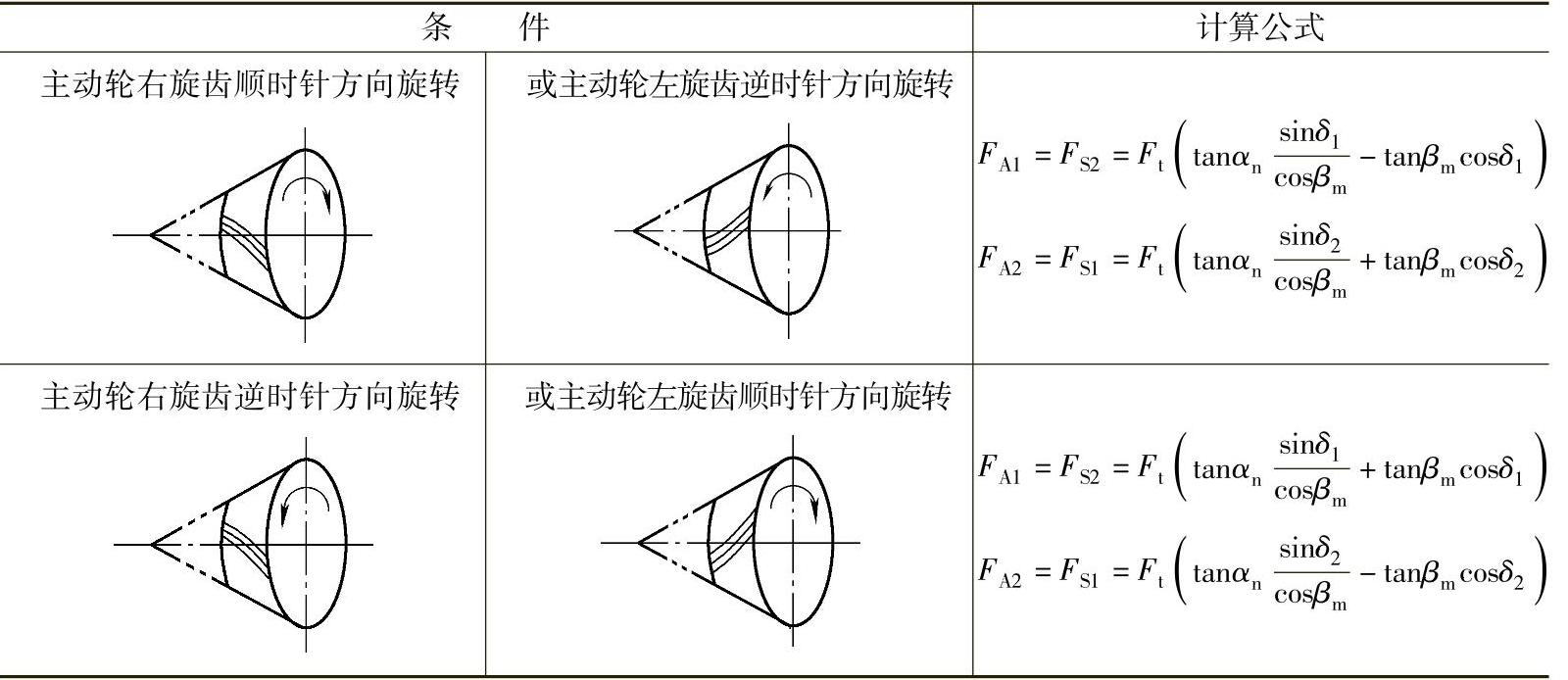
图2-62 确定螺旋伞齿轮轴向力方向的方法

表列公式中：

α_n——齿轮的法面压力角；

δ——齿轮的半节锥角；

β_m——齿宽中点的螺旋角。

表2-50所列公式中，如令：

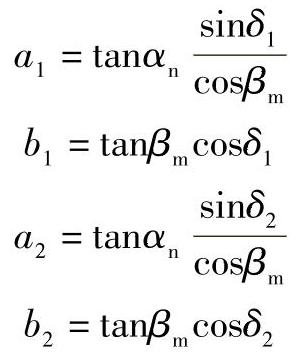
则

主动轮右旋齿顺时针方向旋转时（或主动轮左旋齿逆时针方向旋转时）：

F_A1=F_s2=F_t（a₁-b₁）

F_A2=F_s1=F_t（a₂+b₂）

主动轮右旋齿逆时针方向旋转时（或主动轮左旋齿顺时针方向旋转时）：

F_A1=F_s2=F_t（a₁+b₁）

F_A2=F_s1=F_t（a₂-b₂）

根据给定的α_n、δ、β_m，可以由上述公式计算出相应的a₁、a₂、b₁、b₂的数值，然后再计算出轴向力和向心力的数值。

5.蜗轮传动

蜗轮传动的作用力如图2-63所示。在蜗轮传动中蜗杆的圆周力F_t1与蜗轮的轴向力F_A2方向相反数值相等。蜗杆的轴向力F_A1与蜗轮的圆周力F_t2方向相反数值相等。

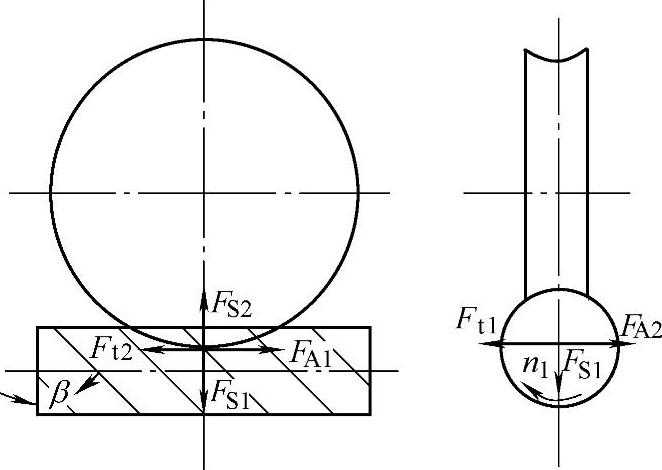
图2-63 蜗轮传动的作用力

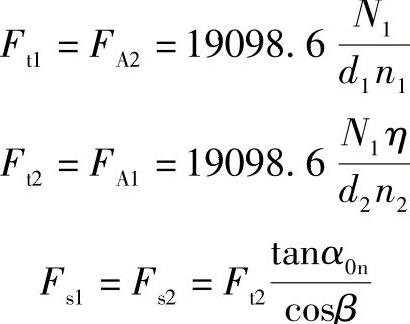
式中 F_t1——蜗杆的圆周力（kN）；

F_t2——蜗轮的圆周力（kN）；

F_A1——蜗杆的轴向力（kN）；

F_A2——蜗轮的轴向力（kN）；

F_s1——蜗杆的向心力（kN）；

F_s2——蜗轮的向心力（kN）；

N₁——蜗杆的传动功率（kW）；

η——传动效率；

α_0n——法面压力角；

β——蜗杆的螺旋角；

d₁——蜗杆节圆直径（mm）；

d₂——蜗轮节圆直径（mm）；

n₁——蜗杆转速（r/min）；

n₂——蜗轮转速（r/min）。

6.带传动

带传动中，传动力F_t可由下式求出：

式中 N——传动功率（kW）；

d——带轮直径（mm）；

n——带轮转速（r/min）。

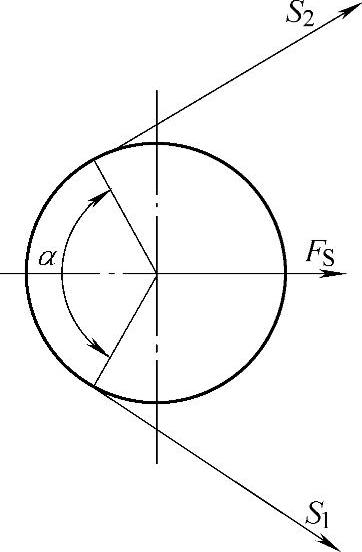
图2-64 皮带传动的作用力

传动力F_t是带紧边和松边张力之差，所以如果用S₁表示紧边拉力，S₂表示松边拉力，则F_t=S₁-S₂，如图2-64所示。因此带作用于轴上的向心力F_s与初拉力、包角和转速有关。一般近似计算可由传动力F_t乘以经验系数而得，即

F_s=f_bF_t

式中 F_t——带的传动力；

F_s——带作用于轴上的力；

f_b——带系数，列于表2-51中；

表2-51 带系数fb

注：两轴中心距较小，转速较低时应取较大值。