滚动轴承振动按产生机理可分为以下三种类型:轴承结构的固有振动1)把外圈看作是弹性体引起的固有振动,如表5-1所示。表5-1 套圈弹性固有振动类型表5-2 套圈刚体固有振动类型表5-3 滚动体固有振动强迫振动1)滚动体通过振动 当轴承运转时滚动体周期通过载荷作用线引起的振动,如表5-4所示。表5-6 滚道表面缺陷引起的轴承振动频率滚动轴承的振动往往是以上各类振动共同作用的结果。......
2023-06-26
1.基本概念
图2-50表示塑性变形的示意图。三个直径相同的钢球在载荷Q的作用下,钢球Ⅰ、Ⅲ的中心距由l减小到l1,这时钢球Ⅰ上的a点和钢球Ⅱ上的b点、钢球Ⅱ上的c点和钢球Ⅲ上的d点互相趋近。两个接触处总的趋近量为
δ=l-l1
如果趋近量δ为弹性变形造成的话,则在去掉载荷Q后,其中心距应恢复到l。但是实际上中心距并不恢复到l而是到l2。这就说明,在载荷Q的作用下钢球Ⅰ、Ⅱ和Ⅱ、Ⅲ之间的接触变形不完全是弹性变形,而有塑性变形存在。塑性变形量为
δs=l-l2
根据Hertz弹性接触理论,点接触时弹性变形与载荷Q2/3成正比,在图2-51中应为虚线所示的直线,但实际测得的变形曲线却为实线所示的曲线。图2-51表明,载荷较轻时,接触变形量主要是弹性变形。随着载荷的增大,塑性变形量也逐渐增大。如果载荷超过一定数值后,塑性变形量明显的增大。图2-52为塑性变形δs与载荷Q关系的示意图。
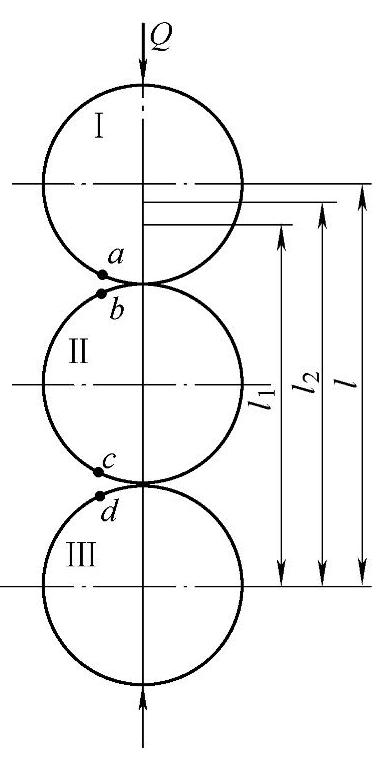
图2 - 50 塑性变形示意图
滚动轴承中塑性变形的形式是在接触面处形成局部凹坑。实验证明,即使在很小的载荷作用下,轴承中也产生塑性变形。在很小载荷作用下就产生塑性变形的主要原因是接触表面并不是理想的光滑表面,而是凸凹不平的粗糙表面。当两物体在载荷作用下互相接触时,首先接触的是凸起的高点,因为这些高点的面积很小,所以即使在很小载荷的作用下,其单位面积上承受的压力已超过材料的弹性极限,故可使高点的材料产生塑性变形而逐渐变平。
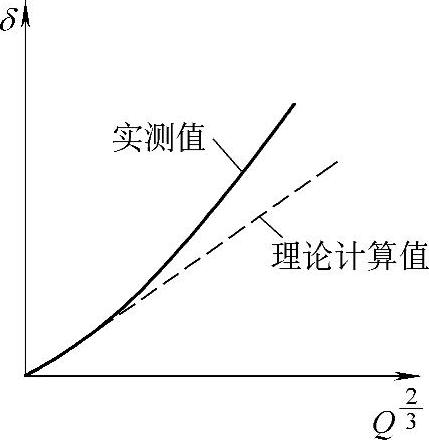
图2-51 δ与Q2/3的关系图
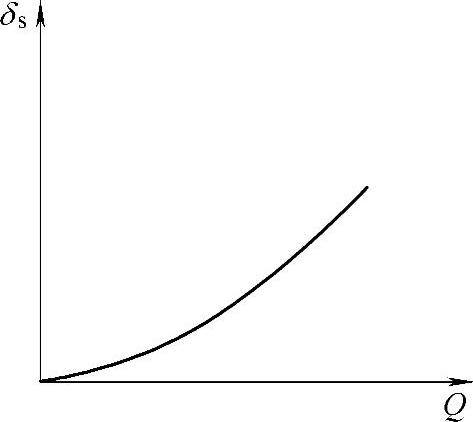
图2-52 塑性变形δs与载荷Q的关系图
2.塑性变形的计算公式
滚动轴承中塑性变形的计算公式为
对点接触:
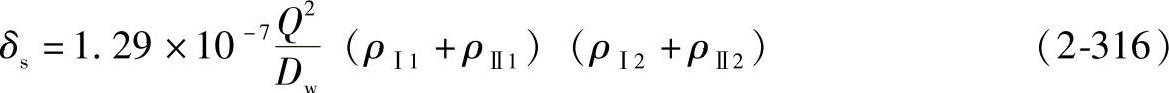
式中 δs——滚动体和一个滚道接触处总的塑性变形量(mm);
Q——滚动体载荷(N);
Dw——滚动体直径(mm);
ρⅠ1;ρⅡ1;ρⅠ2;ρⅡ2——接触物体Ⅰ、Ⅱ在主平面1、2中的主曲率(1/mm)。对线接触:
在线接触情况下,滚子和滚道接触处的塑性变形量,沿滚子长度方向是不一样的。滚子中部塑性变形较小,接触端部的塑性变形较大,尤其是套圈滚道长度大于滚子长度时更是如此。这时接触区内最大的总的塑性变形量为
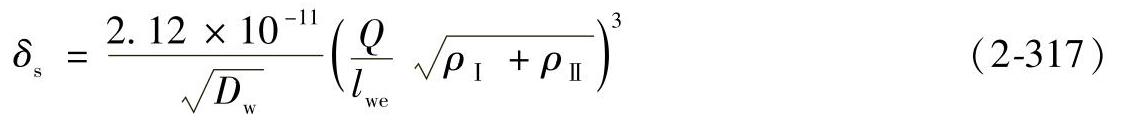
式中 δs——滚子最大塑性变形量(mm);
lwe——有效接触长度(mm);
ρⅠ、ρⅡ——接触物体Ⅰ、Ⅱ的主曲率(1/mm)。
轴承中塑性变形量的分布,大致是: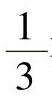 在滚动体上,
在滚动体上,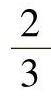 在滚道上。
在滚道上。
有关滚动轴承应用手册的文章

滚动轴承振动按产生机理可分为以下三种类型:轴承结构的固有振动1)把外圈看作是弹性体引起的固有振动,如表5-1所示。表5-1 套圈弹性固有振动类型表5-2 套圈刚体固有振动类型表5-3 滚动体固有振动强迫振动1)滚动体通过振动 当轴承运转时滚动体周期通过载荷作用线引起的振动,如表5-4所示。表5-6 滚道表面缺陷引起的轴承振动频率滚动轴承的振动往往是以上各类振动共同作用的结果。......
2023-06-26

选择滚动轴承配合之前,必须首先确定轴承的精度等级。2)载荷大小滚动轴承套圈与轴或壳体孔配合的最小过盈取决于载荷的大小。表6-4向心轴承和轴承座孔的配合——孔公差带注:a.并列公差带随尺寸的增大从左至右选择。图6-6滚动轴承零件图标注表6-8轴和轴承座孔的几何公差续表表6-9配合表面及端面的表面粗糙度任务实施按给定条件,可知Pr=0.125Cr,属于正常负荷。......
2023-06-15

以上公式适用于下列轴承工作条件:1)作用于轴承上的轴向载荷是连续作用的稳定载荷。因此,短圆柱滚子轴承不能用来承受纯轴向载荷,即在承受轴向载荷的同时,还必须承受径向载荷才能正常工作。轴向载荷的性质,也直接影响短圆柱滚子轴承的轴向承载能力。一般来说,间断作用的轴向载荷能改善轴承的润滑条件,因而轴承承受间断作用的轴向载荷能力比上述公式计算值提高1~2倍。......
2023-06-26

任务要求1.了解滚动轴承的结构及其特点。图4.52减速器3.能合理地进行滚动轴承的组合设计。滚动轴承的代号由前置代号、基本代号和后置代号3个部分代号所组成。表4.15滚动轴承代号尺寸系列代号尺寸系列代号是由轴承的直径系列代号和宽(高)度系列代号组合而成,用两位数字表示。......
2023-06-30

如果轴承的实际载荷条件与确定额定静载荷的假定条件不同,则应将实际载荷换算为当量静载荷后才能与额定静载荷相比较。图中的曲线表示,为了得到相同的当量静载荷P0的Fr与Fa相对关系。用角注Ⅰ、Ⅱ表示轴承中的两列,并且假定Ⅰ列承受较重的载荷,即假定Ⅰ列的塑性变形量较大,因此只用QmaxⅠ来计算轴承的当量静载荷。......
2023-06-26
相关推荐