如果轴承的实际载荷条件与确定额定静载荷的假定条件不同,则应将实际载荷换算为当量静载荷后才能与额定静载荷相比较。图中的曲线表示,为了得到相同的当量静载荷P0的Fr与Fa相对关系。用角注Ⅰ、Ⅱ表示轴承中的两列,并且假定Ⅰ列承受较重的载荷,即假定Ⅰ列的塑性变形量较大,因此只用QmaxⅠ来计算轴承的当量静载荷。......
2023-06-26
由上节所述可知,滚动轴承的额定动载荷是在假定的运转条件下确定的。即对向心轴承是指内圈旋转、外圈静止时的径向载荷;对推力轴承是指中心轴向载荷;对向心推力轴承是指使轴承半圈滚道受载的载荷的径向分量。
如果作用于轴承上的实际载荷与假定的条件不同,则必须把实际载荷转换为与确定额定动载荷的运转条件相同的假定载荷。在此假定载荷的作用下,轴承的寿命和实际载荷条件下的寿命相同,因此把此假定载荷称为当量动载荷,用P表示。
6.4.1 滚动轴承额定寿命的计算公式
在式(2-188)中给出了额定寿命与额定滚动体载荷和实际滚动体载荷之间的关系

式中 Qc——额定滚动体载荷;
Q——实际滚动体载荷;
ε——寿命指数。
如果用Li、Le分别表示滚动体与内、外圈接触处的额定寿命,则

式中,Qi和Qe为内、外圈接触处的平均滚动体载荷。由式(2-211)、式(2-212)和载荷分布理论可得
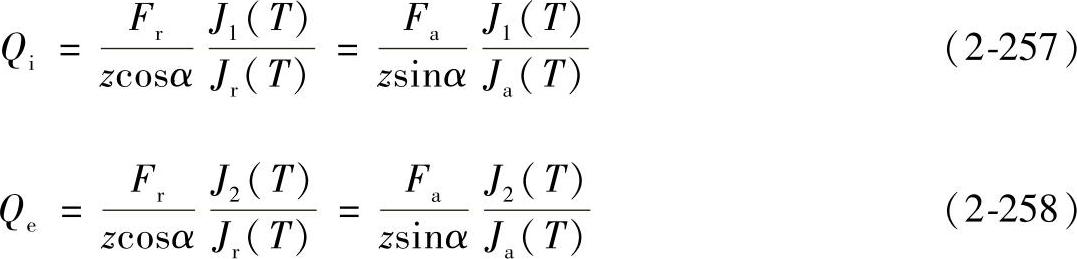
由式(2-213)和式(2-214)可得

将式(2-257)~式(2-260)代入式(2-255)、式(2-256)中可得
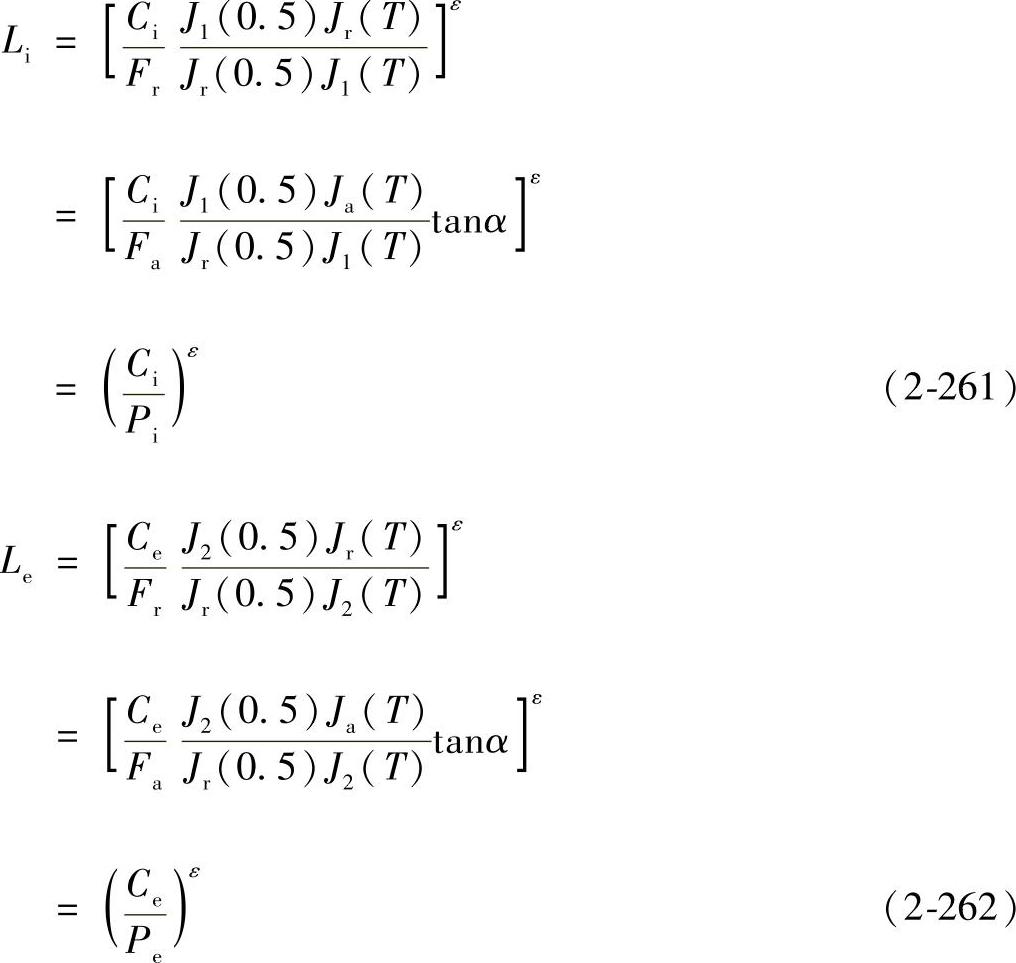
由式(2-261)和式(2-262)可得

Pi和Pe分别称为内圈和外圈的当量动载荷。
在式(2-220)和式(2-221)中,如Fr分别为内圈和外圈的当量动载荷Pi和Pe,则可得
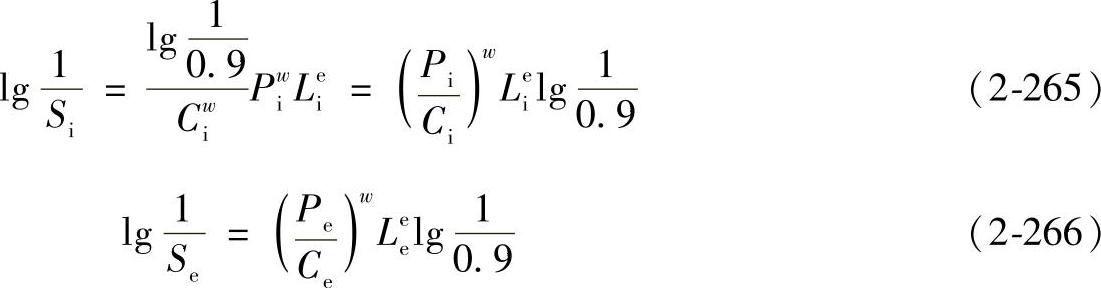
由概率乘积可得

对同一轴承来说:Li=Le=L
所以可得

把Pi和Pe的式(2-263)和(2-264)代入可得
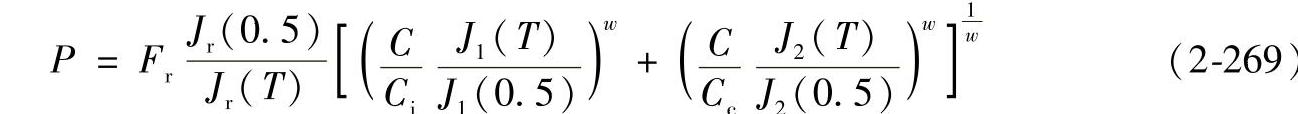
或
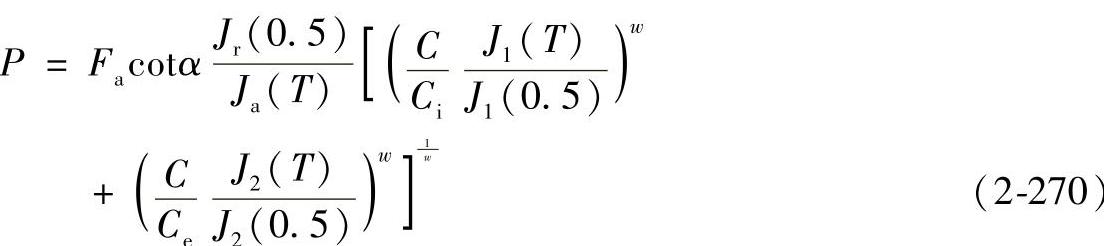
由式(2-267)可得轴承的额定寿命计算公式为

式中 L——额定寿命(百万转);
C——额定动载荷(N);
P——当量动载荷(N);
ε[3]——寿命指数,有
对球轴承:ε=3
对滚子轴承
式(2-271)为滚动轴承寿命计算的基本公式。
式(2-269)或式(2-270)是滚动轴承当量动载荷计算的基本公式。由式(2-269)或式(2-270)可看出,当量动载荷是径向载荷Fr和轴向载荷Fa的函数。对一给定的轴承类型来说,首先由Fr和Fa确定轴承中的载荷分布参数T,然后才能用式(2-269)或式(2-270)计算出与Fr和Fa相应的当量动载荷P。这样复杂的计算过程在使用中很不方便,因此下面讨论在一定的简化条件下,推导比较方便实用的当量动载荷计算公式。
6.4.2 单列轴承的当量动载荷
由式(2-269)和式(2-270)可得
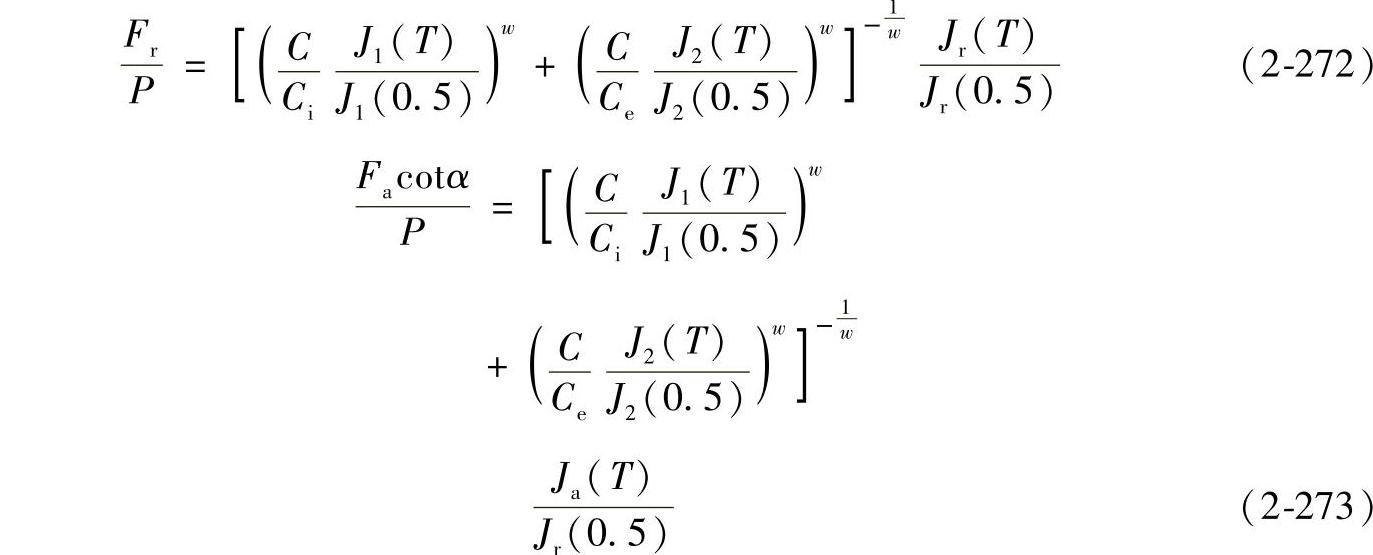
由式(2-272)和式(2-273)可看出, 和
和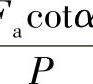 仅与载荷分布参数T有关。图2-43和图2-44分别表示点接触和线接触情况下
仅与载荷分布参数T有关。图2-43和图2-44分别表示点接触和线接触情况下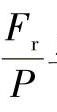 与
与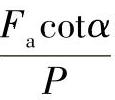 的关系,图中两条曲线分别表示
的关系,图中两条曲线分别表示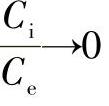 和
和 的极端情况。
的极端情况。
图2-43和图2-44的曲线还可以表示为了得到相同的当量动载荷P,径向载荷Fr与轴向载荷Fa之间的关系。
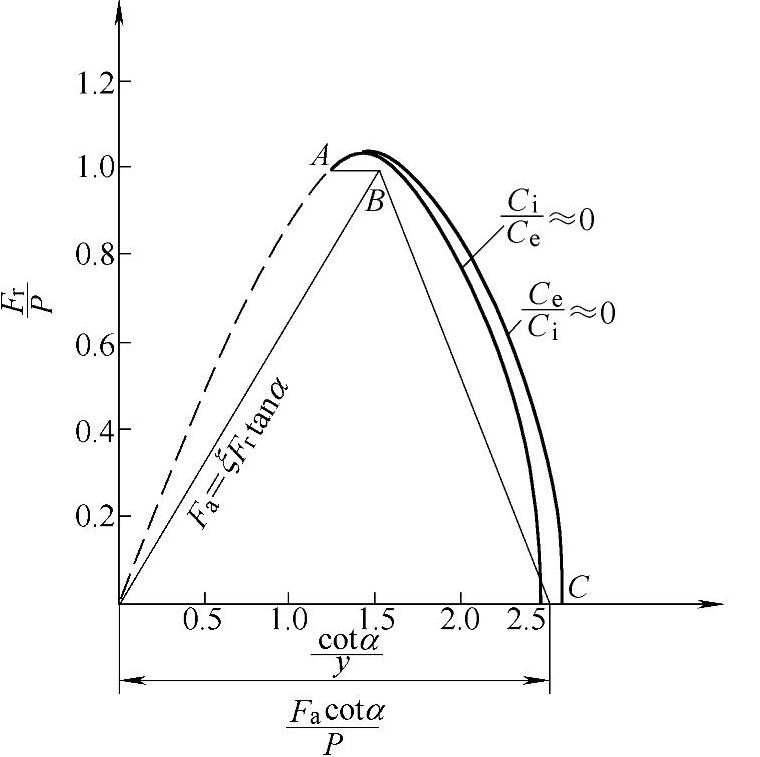
图2-43 点接触时Fr与Fa的关系
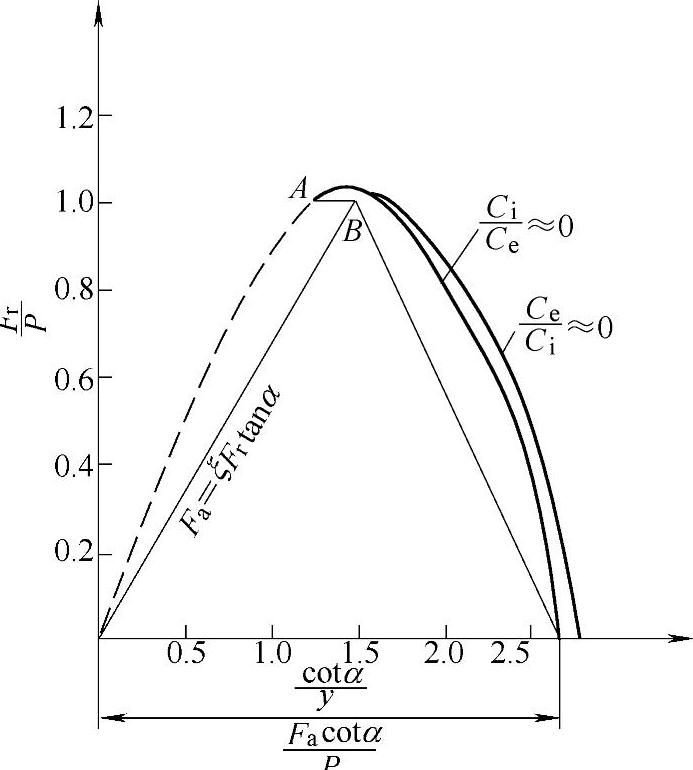
图2-44 线接触时Fr与Fa的关系
为了简化当量动载荷P的计算,把图中的曲线用折线AB和BC代替。AB线段与BC线段的交点B的坐标为
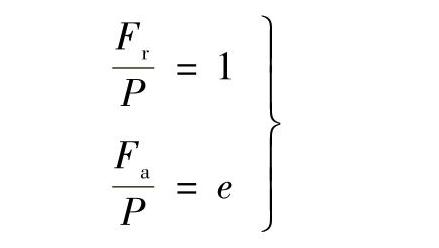
所以可得B点的Fa与Fr的关系为
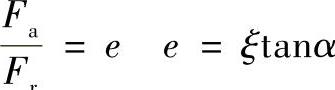
其中ξ是与轴承类型有关的常数,e是与ξ和接触角α有关的参数。
当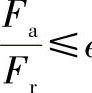 时用AB线段的方程计算当量动载荷P。
时用AB线段的方程计算当量动载荷P。
当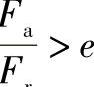 时用BC线段的方程计算当量动载荷P。
时用BC线段的方程计算当量动载荷P。
当Fa与Fr的相对数值小于A点的数值时,轴承中承受载荷的滚动体数目减少,使轴承不能正常工作,因此A点左边的曲线用虚线表示。
当量动载荷P可用统一的公式计算:
P=XFr+YFa (2-274)
对AB线段:X=1 Y=0
对BC线段:可由B点和C点的坐标来计算。
C点的坐标为

代入式(2-274)中可得
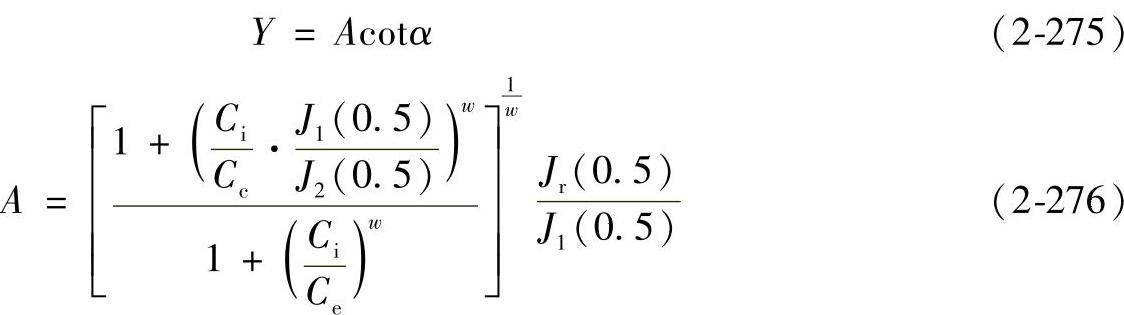
对不同的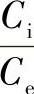 的数值,可以计算出A值,但发现A值的变化范围很小,因此对点接触和线接触可统一取为
的数值,可以计算出A值,但发现A值的变化范围很小,因此对点接触和线接触可统一取为
A≈0.4
所以Y=0.4cotα (2-277)
B点的坐标为
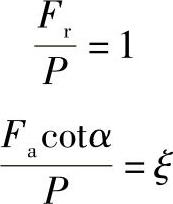
代入式(2-274)中可得
X=1-Ye (2-278)
对向心球轴承 ξ=1.1
向心推力球轴承 ξ=1.25
向心滚子轴承 ξ=1.5
6.4.3 向心和向心推力球轴承的当量动载荷
多数类型的轴承,可以认为接触角与载荷无关。对于向心球轴承和向心推力球轴承,其接触角是随载荷而变化的,尤其是名义接触角很小时或承受纯轴向载荷时,接触角变化比较显著。因此在确定这些类型轴承的当量动载荷P时,必须考虑接触角的变化。
向心推力球轴承和向心球轴承,在同时承受径向载荷和轴向载荷时,接触角是随滚动体的位置而不同的。为了简化当量动载荷的计算,在确定这类轴承当量动载荷时,首先计算在轴向载荷作用下的实际接触角α,然后将α值代入式(2-277)和式(2-278)中,计算出X、Y和e值。
向心球轴承和向心推力球轴承实际接触角的计算公式为
向心球轴承:

向心推力球轴承:
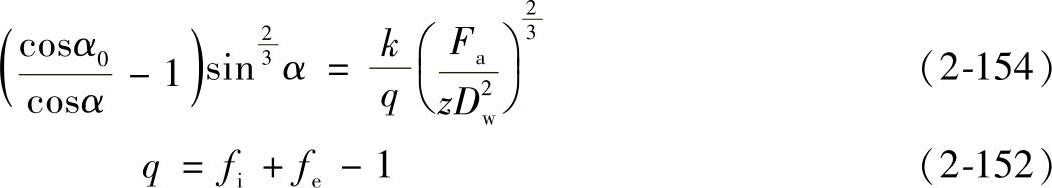
式中 α0——名义接触角(或初始接触角);
α——在轴向载荷Fa作用下的实际接触角;
k——轴承弹性变形常数,可由表2-7或图2-16中查出;
Fa——轴向载荷(kN);
Dw——滚动体直径(mm);
z——滚动体数量。
我国标准设计的单列向心球轴承取fi=fe=0.515,而滚道沟曲率半径取正公差,因此实际上f在0.515~0.52之间。如取其平均值:
fi=fe=0.5175
则由表2-7中可查得
k=0.000437
由式(2-152)可得
q=0.035
在式(2-155)中,z、Dw都是轴承的内部结构尺寸,在一般轴承样本和手册中是查不到的,但可查到额定静载荷C0的数值,而
C0=1.25zD2w
将k、q、C0代入式(2-155)中可得

将式(2-279)代入式(2-277)和式(2-278)中,可得单列向心球轴承的e、X、Y数值为
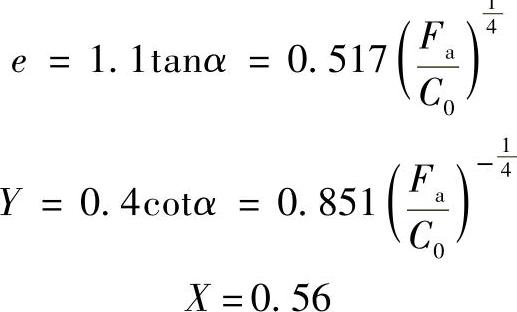
常用的 范围内的Y、e数值列于表2-26和图2-45、图2-46中
范围内的Y、e数值列于表2-26和图2-45、图2-46中
各类单列轴承X、Y、e的计算公式列于表2-27中。
表2-26 单列向心球轴承的e、Y

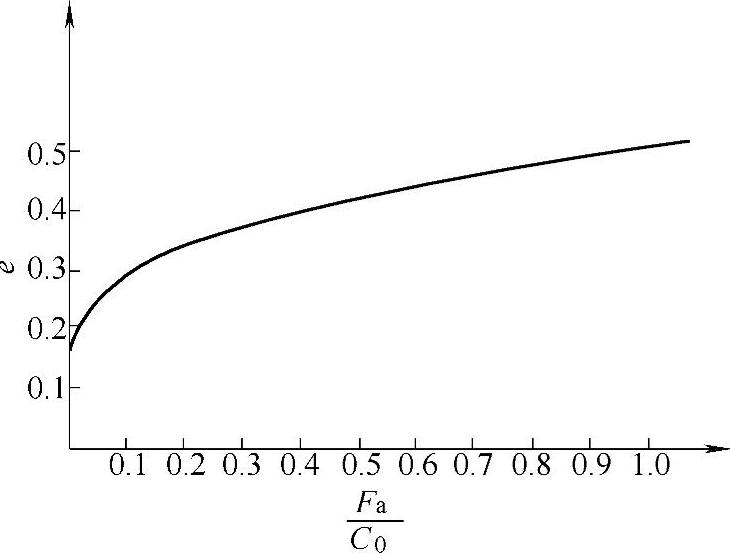
图2-45 单列向心球轴承的e值
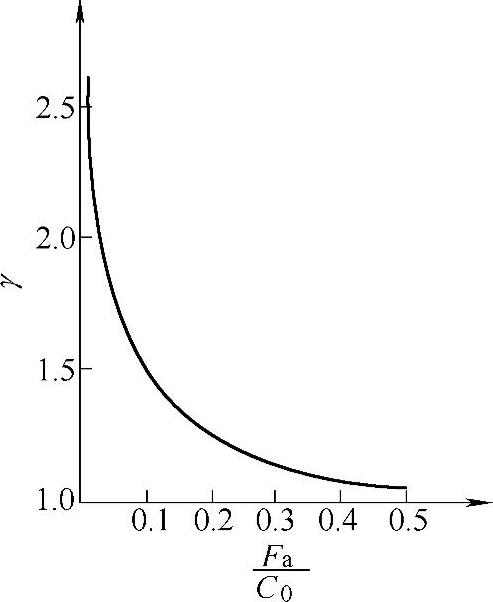
图2-46 单列向心球轴承的Y值
表2-27 单列轴承的α、e、X、Y计算公式
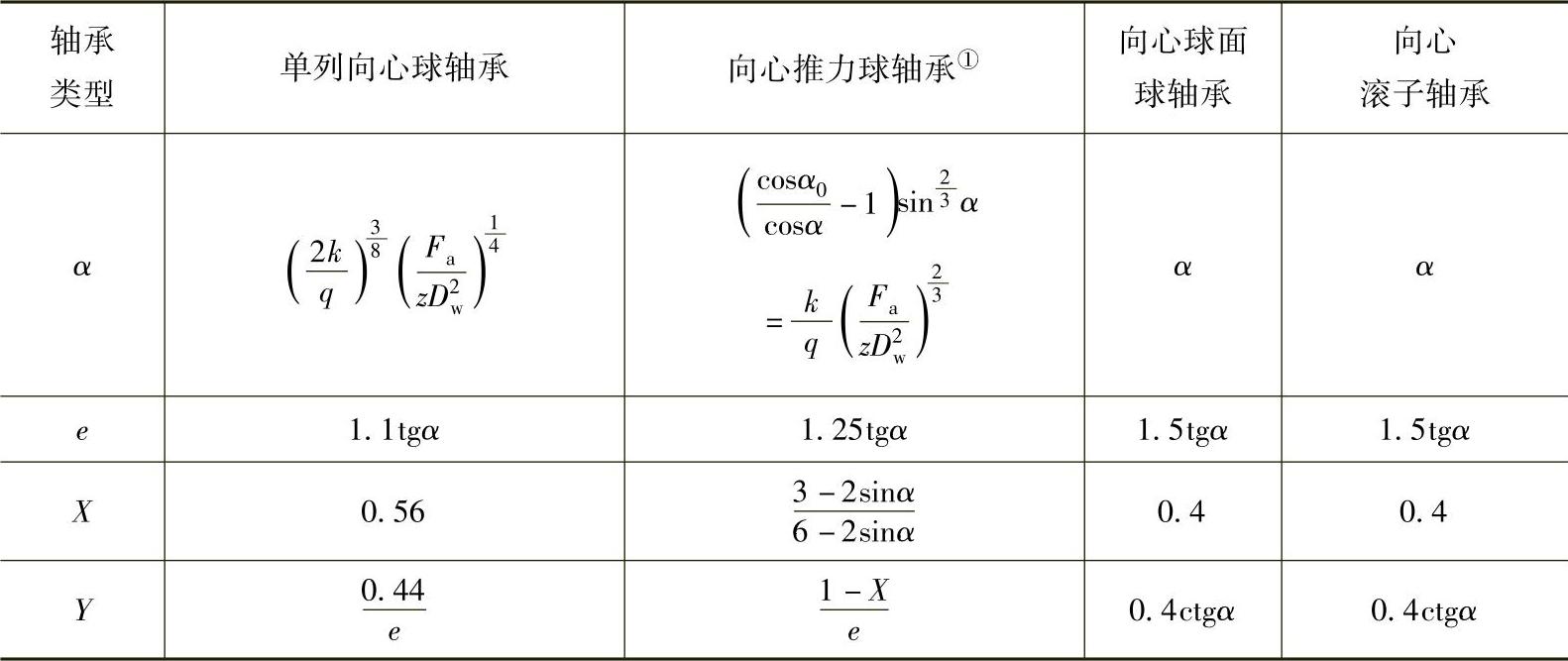
①向心推力球轴承在承受轴向载荷时,由于制造误差(如滚道壁厚差、滚道侧摆),使轴承的实际当量动载荷比理论计算值要高。一般是在轴向系数Y中引入一经验系数η,η= 。所以对向心
。所以对向心
推力球轴承: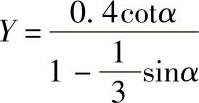
6.4.4 双列向心推力轴承的当量动载荷
这里讨论的双列轴承,是指对称的接触角为α的双列向心推力轴承,如向心球面球轴承、向心球面滚子轴承、双列圆锥滚子轴承、成对安装的向心推力球轴承(外圈宽窄端面相对,即串联配置的除外)。
(1)双列轴承的“平均”载荷和单列轴承一样,假定:内圈相对于载荷向量旋转,外圈相对于载荷向量静止。下标Ⅰ、Ⅱ分别表示轴承中的两列。
用Si表示整个内圈的使用概率;SiⅠ、SiⅡ表示内圈Ⅰ、Ⅱ列的使用概率。由式(2-207)可得

对整个内圈来说,有
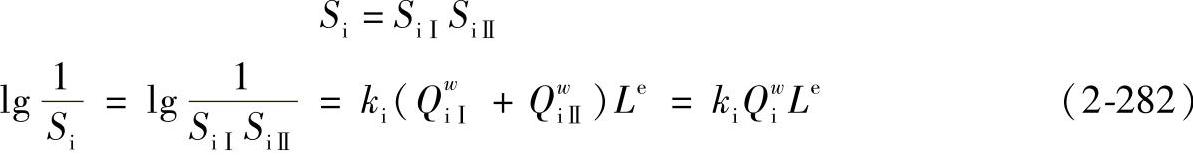
式中 
用TⅠ、TⅡ分别表示轴承中两列的载荷分布参数,则由式(2-211)可得

所以
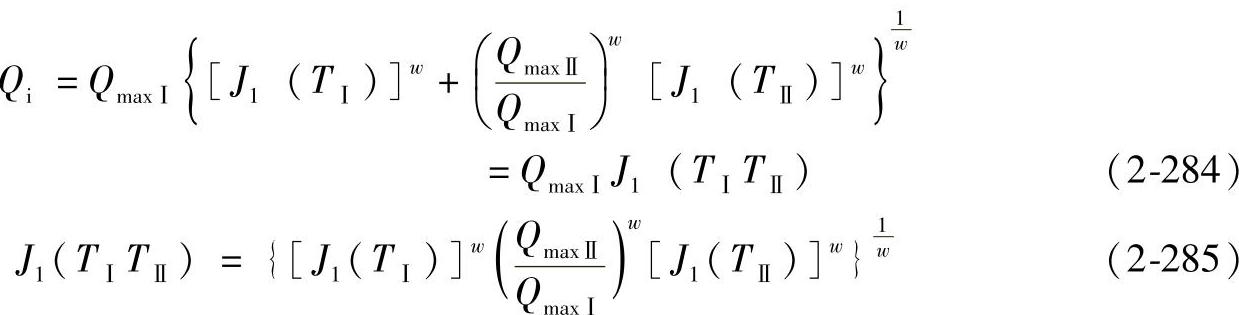
对静止的外圈,同理可得

Qi、Qc称为双列轴承内圈、外圈的“平均”载荷。如将式(2-102)代入式(2-284)和式(2-286)中,则可得
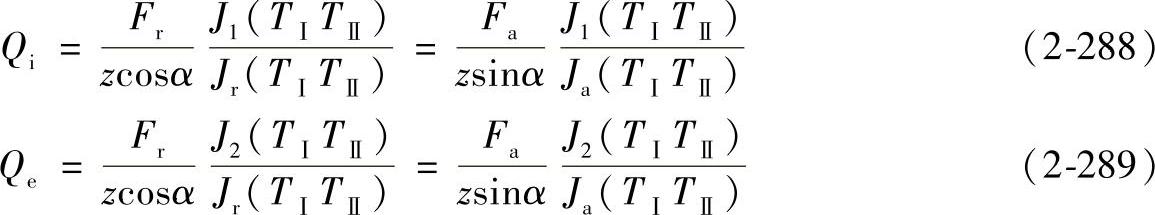
J1(TⅠTⅡ)和J2(TⅠTⅡ)之值列于表2-28中。
(2)双列轴承的当量动载荷 和单列轴承一样,可以作出双列轴承的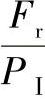 和
和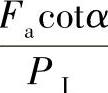 的关系图2-47和图2-48。
的关系图2-47和图2-48。
图中 Fr——作用于双列轴承上的径向载荷;
Fa——作用于双列轴承上的轴向载荷;
PⅠ——相应的单列轴承的当量动载荷;
YⅠ——单列轴承的轴向系数。
表2-28 双列轴承的J1(TⅠTⅡ)、J2(TⅠTⅡ)
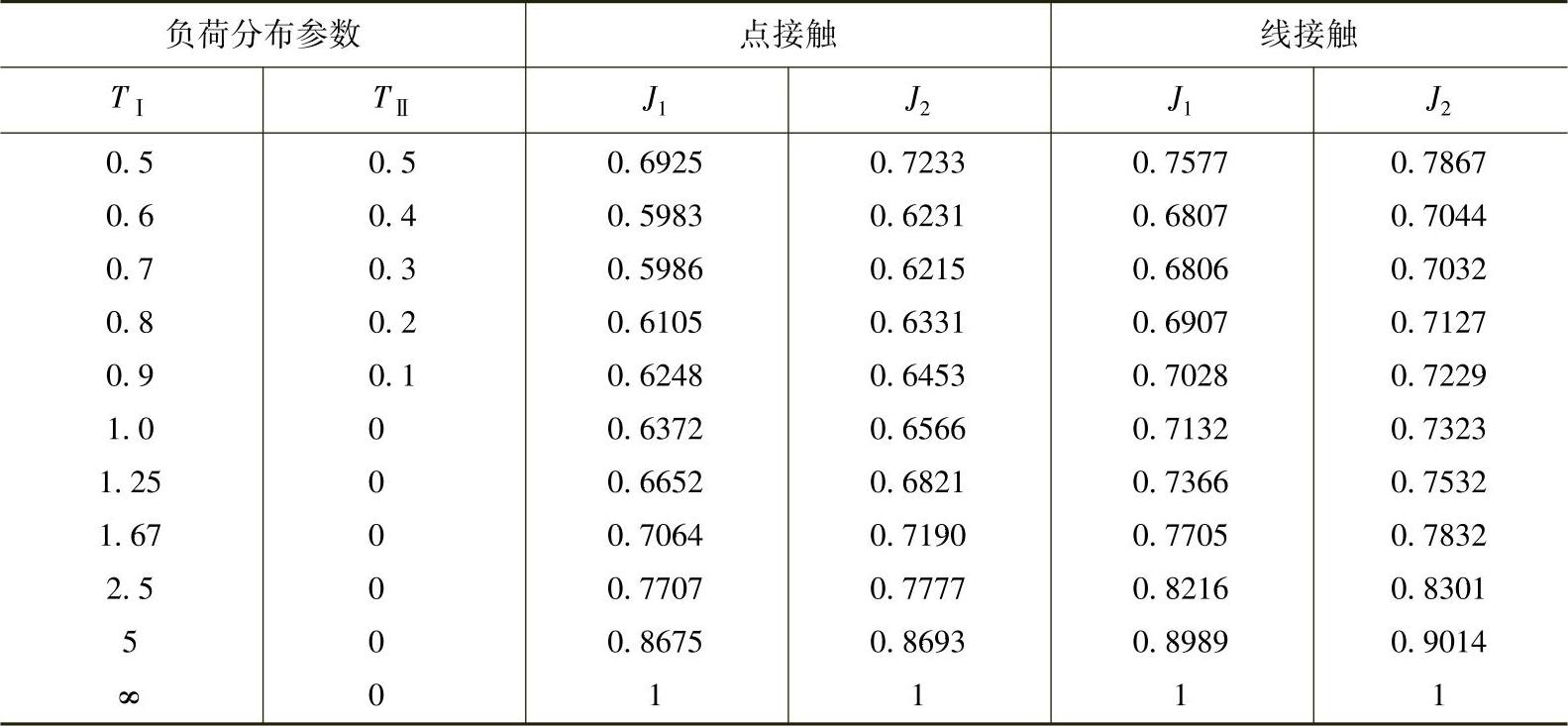
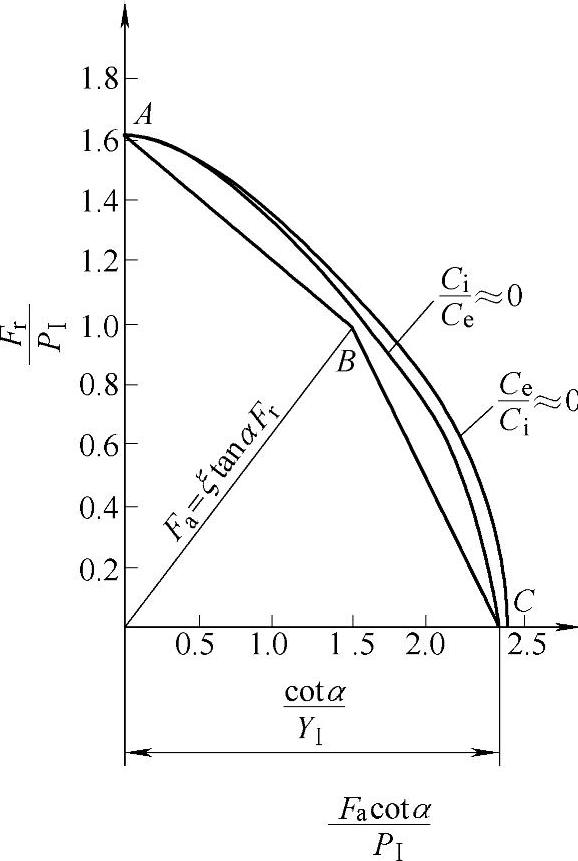
图2-47 点接触Fr与Fa的关系

图2-48 线接触Fr与Fa的关系
图2-47和图2-48中的曲线表示为了得到相同的当量动载荷P,径向载荷Fr和轴向载荷Fa之间的关系。为了简化当量动载荷的计算,把图中的曲线用线段AB和BC代替。
AB和BC线段的方程可统一写为
P=XFr+YFa (2-274)但对AB和BC线段取不同的X、Y的数值。
1)BC段的X、Y值。AB段与BC段的交点B的坐标为
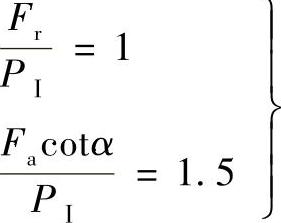
与B点相对应的径向载荷Fr和轴向载荷Fa的关系为
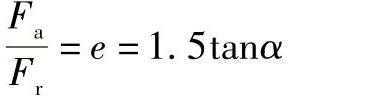
当 时,应用BC段的方程计算当量动载荷。
时,应用BC段的方程计算当量动载荷。
接触角为α的双列轴承,可以承受任意方向的载荷。随着载荷方向的变化,两列中的载荷分布也随之变化。如果一个纯径向载荷Fr作用在轴承上,则两列承受相同的载荷。如果径向载荷Fr和轴向载荷Fa同时作用在轴承上,则随着载荷角的增大,其中一列的载荷区增大,另一列的载荷区减小。由表2-13可看出:当
球轴承 Fa﹥1.67Frtanα
滚子轴承 Fa﹥1.91Frtanα
时,则只有一列滚动体承受载荷,另一列滚动体不承受载荷,这时双列轴承便象单列轴承那样起作用。这时轴承的寿命可以按单列轴承来计算,也可按双列轴承来计算,结果应相同。
用PⅠ、CⅠ、XⅠ、YⅠ分别表示单列轴承的数值;用P、C、X、Y分别表示双列轴承的数值,则可得

所以
对球轴承:P=1.62PⅠ
对滚子轴承P=1.71PⅠ
而PⅠ=XⅠFr+YⅠFa
P=XFr+YFa
将式(2-290)代入可得

将式(2-277)和式(2-278)代入可得
对球轴承:

对滚子轴承:

2)AB段的X、Y值。当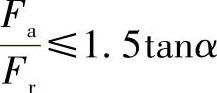 时,应用AB段的方程来计算当量动载荷。这时可用A、B两点的坐标来确定X、Y值。
时,应用AB段的方程来计算当量动载荷。这时可用A、B两点的坐标来确定X、Y值。
对A点可得
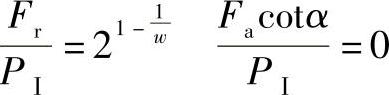
所以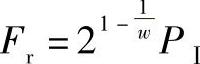
由式(2-290)可得
P=Fr
因此可得 X=1
对B点可得
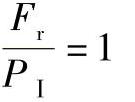
Fa=1.5tanαFr
将上述之值代入式(2-274)中可得
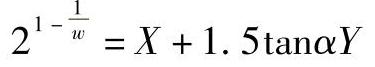
所以 
对球轴承可得

对滚子轴承可得

综上所述将双列向心推力轴承的X、Y、e的计算公式列入表2-29中。
表2-29 双列向心推力轴承的X、Y、e计算公式
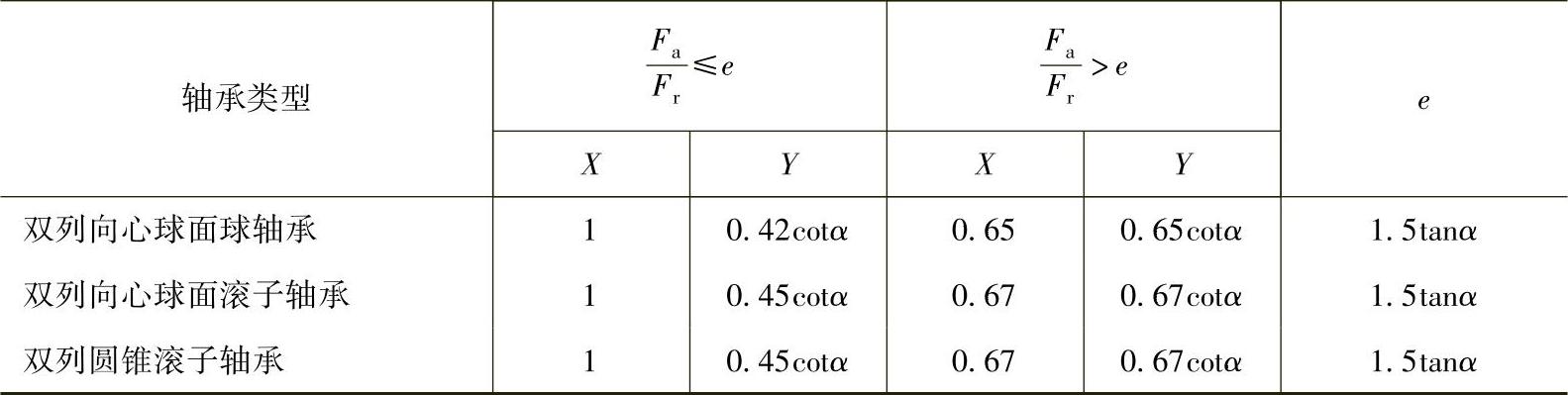
双列向心推力球轴承,在确定当量动载荷P时应考虑接触角的变化,先求出单列轴承的XⅠ、YⅠ,然后用式(2-291)和式(2-292)计算出双列轴承的X、Y值。
6.4.5 推力轴承的当量动载荷
推力和推力向心轴承的额定动载荷是指中心轴向载荷。因而对同时承受轴向载荷和径向载荷的推力轴承,必须将实际载荷转换为当量动载荷P后,才能进行寿命计算。
α=90°的推力轴承,不能承受径向载荷,此类轴承的当量动载荷为
P=Fa (2-298)
但是推力向心轴承,如推力向心球面滚子轴承,可以承受一定的径向载荷。这些轴承主要是承受轴向载荷,所以其额定动载荷是指中心轴向载荷。这类轴承也可以看作是接触角α较大的向心推力轴承,其径向当量动载荷应由式(2-274)计算。如果其径向当量动载荷用Pr表示,径向系数用Xr表示,则由式(2-274)可得
Pr=XrFr+YFa (2-299)
用径向当量动载荷Pr和轴向当量动载荷P计算出的轴承寿命应相同,即
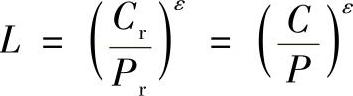
所以 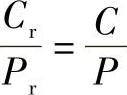
对同一轴承来说,用径向载荷表示的载荷容量和用轴向载荷表示的载荷容量之间的关系应为
Cr=YCa
所以可得用中心轴向载荷表示的当量动载荷为

由式(2-277)和式(2-278)可得

6.4.6 外圈相对于载荷向量旋转时,对当量动载荷的影响
以上在确定额定动载荷C和当量动载荷P时都假定:内圈相对于载荷向量旋转,外圈静止。在这种情况下最大滚动体载荷经常作用在外圈滚道的同一点上,而外圈滚道的其他点则承受较轻的载荷或完全不承受载荷。内圈滚道上的每一点都承受相同的变动载荷。当内圈滚道上的一点进入载荷区时,首先与载荷很轻的滚动体开始接触,继而与载荷较重的滚动体接触,直至承受最大的滚动体载荷,此后该点将逐渐承受较轻的滚动体载荷。
如果与上述假定相反,即外圈相对于载荷向量旋转而内圈静止,则内、外圈所承受载荷的情况与上述假定不同,其平均滚动体载荷的求法也不同。
如果在这种假定条件下用Qi′、Qe′分别表示内、外圈的平均滚动体载荷;Ci′、Ce′分别表示内外圈的额定载荷,则由式(2-205)和式(2-209)可得
Qi′=Qe=QmaxJ2 (2-303)
Qe′=Qi=QmaxJ1 (2-304)
同理可由式(2-213)和式(2-214)可得
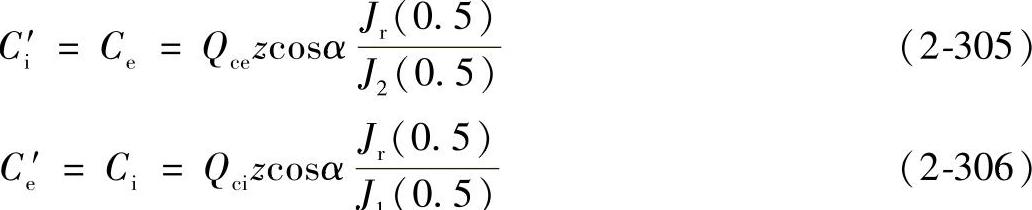
在内圈相对于载荷向量旋转和相对载荷向量静止的两种情况下,内圈滚道的额定滚动体载荷应相同,因而可得

同理可得

如令 
则可得

在载荷分布参数T=0.5时,将式(2-310)和式(2-311)代入式(2-272)中可得

如令
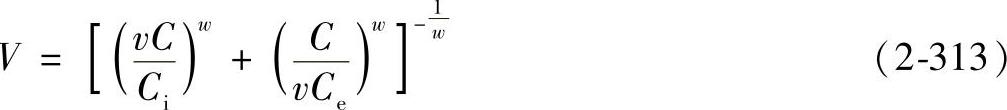
则可得
P=VFr (2-314)
式中,V称为旋转系数。
如将式(2-224)和式(2-225)代入式(2-313)中可得

对不同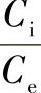 时的V值列于表2-30中
时的V值列于表2-30中
表2-30 旋转系数V
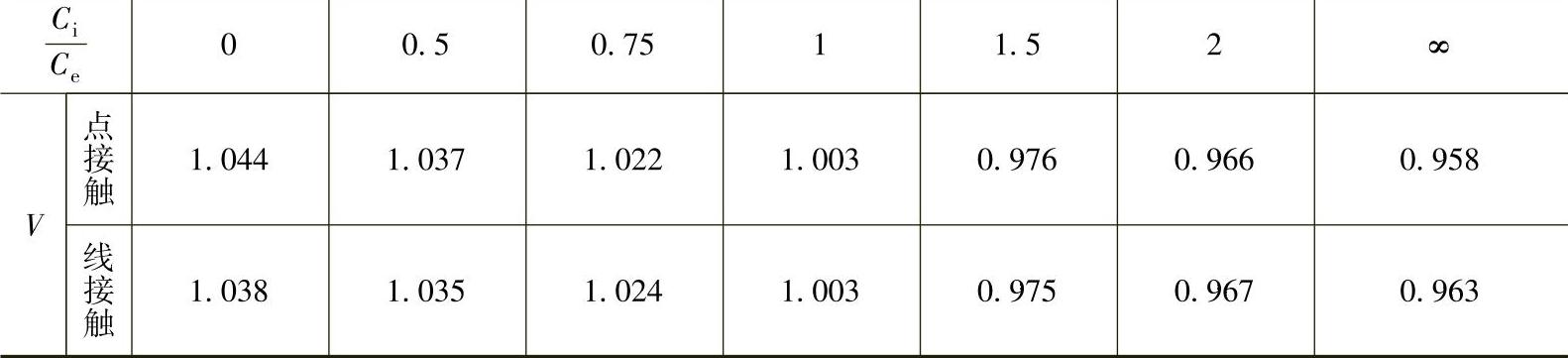
由表列数值可看出旋转系数V最大为1.044(点接触)和1.038(线接触),而实际轴承中,内外圈强度不可能达到这样的数值。因此在实际计算中取V=1,而在当量动载荷计算公式(2-274)中省略不写。
有关滚动轴承应用手册的文章

如果轴承的实际载荷条件与确定额定静载荷的假定条件不同,则应将实际载荷换算为当量静载荷后才能与额定静载荷相比较。图中的曲线表示,为了得到相同的当量静载荷P0的Fr与Fa相对关系。用角注Ⅰ、Ⅱ表示轴承中的两列,并且假定Ⅰ列承受较重的载荷,即假定Ⅰ列的塑性变形量较大,因此只用QmaxⅠ来计算轴承的当量静载荷。......
2023-06-26

所以韦布尔的理论不能直接用来解决滚动轴承的疲劳问题。对滚动轴承接触疲劳起决定作用的,是接触物体内部的剪应力τzy。额定滚动体载荷与轴承寿命的关系 实验证明,在滚动过程中,疲劳裂纹一般发生在与滚动方向平行的平面内。......
2023-06-26

滚动轴承承受的载荷是通过滚动体由一个套圈传向另一个套圈的。即αi=αe由作用于滚动体上载荷的平衡可知,外圈对滚动体作用的载荷Qe与内圈对滚动体的载荷Qi数值相等,方向相反。所以由式(2-1)可得 7307B角接触轴承承受纯轴向载荷Fa=1kN,求作用于每个钢球上的滚动体载荷是多少?图2-4 圆锥滚子轴承的滚动体负荷外圈作用于滚动体上的载荷为内圈作用于滚动体上的载荷分为两部分。......
2023-06-26

把在这种塑性变形条件下确定的轴承静承载能力称为额定静载荷,用C0表示。额定静载荷是在假定的载荷条件下决定的,对向心轴承,额定静载荷是指径向载荷,对向心推力轴承是指使轴承中半圈滚道受载的载荷的径向分量,对推力轴承是指中心轴向载荷。......
2023-06-26

轴承所承受的载荷,主要与各类传动中的作用力有关。从动轮的轴向力方向与主动齿轮相反。图2-58 直齿圆锥齿轮传动图2-59 斜齿圆锥齿轮传动在计算斜齿圆锥齿轮传动的向心力Fs和轴向力FA时必须首先规定如何确定螺旋角的方向及齿轮的旋转方向。因此带作用于轴上的向心力Fs与初拉力、包角和转速有关。......
2023-06-26

多数情况下,可以把双支承轴的结构作为静定问题处理,利用力的平衡方程计算出支承反力,把得出的支承反力作为轴承载荷进行寿命计算。在大多数轴承应用场合下,把双支承轴作为静定问题,已能足够精确地确定轴承所承受的载荷。在这种支承结构中如果轴的刚性较大,仅考虑轴承的变形时,可用下述方法计算轴承载荷。由第2章第3节所述可知,各列承受的载荷大小与轴向载荷Fa和径向载荷Fr的相对数值有关。......
2023-06-26

滚动轴承的寿命是轴承质量的综合反映,因此各国都非常重视滚动轴承的寿命试验工作。大量的寿命试验数据表明,滚动轴承的疲劳寿命是相当离散的。针对轴承疲劳寿命相当离散的特征,表征一批轴承的寿命,必须用数理统计的方法,用寿命试验数据计算出一定使用概率下的特征寿命值。可靠度Re用寿命试验数据得出的L10t与理论计算值L10相比,可得出该批轴承的可靠度。......
2023-06-26

在应力场计算模型中,提取转子发动机各受热零部件在机械载荷下的轴向变形量。由此可以说明,气缸的轴向机械变形量主要是由螺栓预紧力引起的。再对比图3.37与图3.21,气缸的机械变形变化趋势与螺栓预紧力的变化趋势大致相同。图3.39参考点处的前后端盖参考点轴向距离变化分布根据上述机械变形计算结果可知,在螺栓预紧力和缸内气体压力的作用下,气缸轴向方向的尺寸会发生不同程度的减小。......
2023-06-23
相关推荐