滚动轴承额定动载荷的重要性

6.3.1 确定滚动轴承额定动载荷的基本原理

（1）统计处理滚动轴承接触疲劳问题的基本假设 由上节所述可知，滚动轴承的疲劳寿命是相当离散的。“事物发展的根本原因，不是在事物的外部而是在事物的内部，在于事物内部的矛盾性”。对于宏观上看来完全相同的轴承，在相同的外部运转条件下寿命相当离散这一问题，必须从材料内部去寻找原因。

韦布尔（W.Weibull）在大量实验研究的基础上，用数理统计方法处理材料强度问题，创立了材料强度统计理论。但是韦布尔是研究脆性物体的静破坏强度，因此假定一出现裂纹就引起材料破坏。对于滚动轴承的疲劳破坏来说，常常是从宏观来看，接触表面并未出现裂纹，但在表层下已有裂纹出现。所以韦布尔的理论不能直接用来解决滚动轴承的疲劳问题。

伦得伯格（G.Lundberg）和帕尔格恩（A.Palmgren）在韦布尔理论的基础上，提出了滚动轴承动载荷容量的理论，其基本假设如下：

1）滚动轴承的材料不是均质的，材料内部有强度弱点存在。在非金属夹渣和金属晶体结构有缺陷的地方，就形成了材料强度的弱点。载荷作用时，在材料弱点的周围就引起应力集中。在载荷的反复作用下，在弱点周围出现局部的塑性变形和滑移，最终在弱点邻域形成内部裂纹。在继续运转的过程中，内部裂纹逐步扩展至接触表面，产生表层金属剥落。

对滚动轴承接触疲劳起决定作用的，是接触物体内部的剪应力τ_zy。它与滚动方向平行，并在距接触表面深度为z₀处达到最大值。在滚动过程中τ_zy在±τ₀之间变化。因此在研究接触疲劳问题时假定：材料因疲劳而破坏的概率与τ₀有关。τ₀愈大，材料的破坏概率愈大，使用概率愈小。

2）并非材料内部一出现裂纹就导致材料破坏。内部裂纹扩展至接触表面形成疲劳剥落还有一个过程，因此材料的破坏概率与最大切应力τ_zymax=τ₀的深度z₀有关。z₀愈大，材料的破坏概率愈小。

3）材料的疲劳破坏是逐渐产生的，因此破坏概率与应力循环次数N有关，N愈大，破坏概率愈大。

4）对承受载荷的接触物体，仅在应力幅最大处的邻域中，破坏的危险性最大。因此，破坏概率与材料弱点的数目有关。在应力所及的体积内，弱点数量愈多破坏概率愈大。从统计观点来看，体积愈大则所包含的弱点数量就愈多。因此可把应力所及的体积大小作为弱点数量多少的度量，即应力体积愈大，材料的破坏概率愈大。

在上述几点假设的基础上，提出了统计处理接触疲劳问题的指数方程为

式中 S——材料能经受N（百万次）应力循环的使用概率；

τ₀——接触表面下与滚动方向平行的切应力幅值；

z₀——τ₀所处的深度；

V——应力所及的体积；

c、e、h——待定指数，其中e为韦布尔分布斜率。

在滚动轴承中滚动体与内、外圈都接触，情况比较复杂。为了简化起见，可近似假定：滚动体由于与内圈滚道接触的破坏概率与内圈滚道的破坏概率相等，滚动体由于与外圈滚道接触的破坏概率与外圈滚道的破坏概率相等。在下面的讨论中，只讨论内圈和外圈的破坏概率。

（2）额定滚动体载荷与轴承寿命的关系 实验证明，在滚动过程中，疲劳裂纹一般发生在与滚动方向平行的平面内。由第2章2.4节可知切应力幅τ₀和z₀：

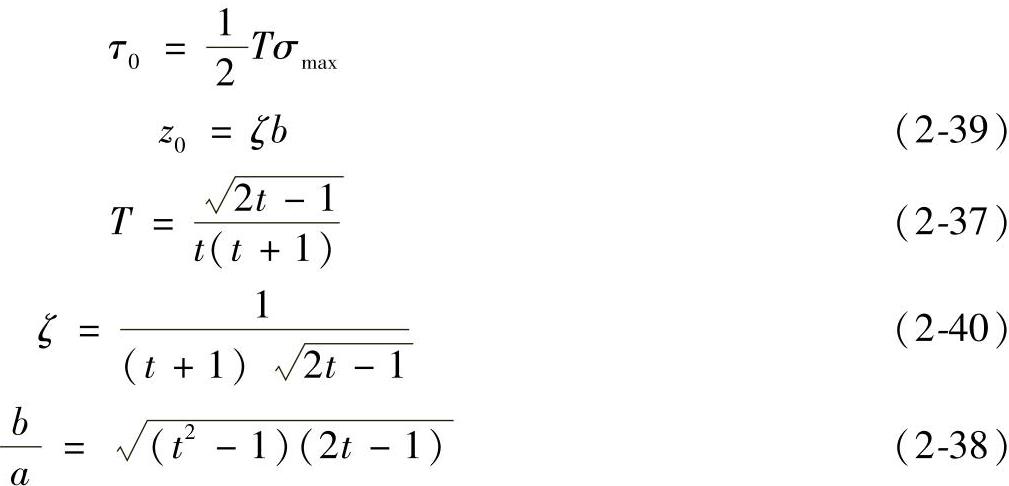
式中 σ_max——接触面上最大压应力；

T、ζ——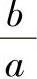的函数；

t——辅助参数。

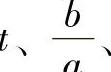T的数值可由表2-6查出。

由赫兹（Hertz）理论可

式中 Q——滚动体载荷（N）；

Σρ——曲率总和；

E——材料弹性模量（N/mm²）；

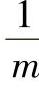——材料的泊桑比；

μ、ν——决定接触椭圆长、短半轴的系数。与函数F（ρ）有关。

在这里是假设两接触物体的材料相同，所以取相同的E和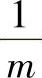值。

1）应力体积V。对应力所及体积，伦得伯格（G.Lundberg）、帕尔格恩（A.Palmgren）提出：

V∝az₀l （2-173）

式中 l——滚道长度。

显然，a、z₀、l三个量，分别表示应力在接触体的宽度、深度和长度三个方向的扩展。

对点接触可取：

V∝πD_naz₀ （2-174）

对线接触可取：

式中 l_we——滚子的有效接触长度；

D_n——接触处滚道直径。

2）应力循环次数N。N是以百万次为单位的应力循环次数，用L表示轴承以百万转为单位的寿命，u表示滚动接触次数，则

N∝uL

将上述τ₀、z₀、V、N代入式（2-169）中，并引入滚动体直径，使

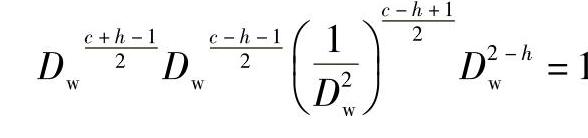
可得

式（2-176）对点接触和线接触都适用。

对点接触将式（2-170）代入式（2-176）中可得

对线接触：因为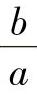很小，取极限值可得

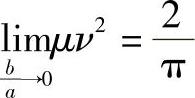
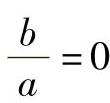时T和ζ的值用T₀ζ₀表示，可得

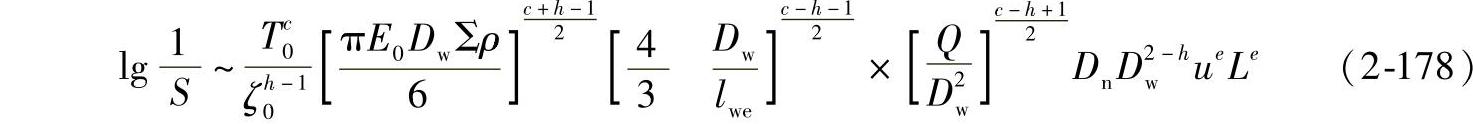
在实际应用中，S为某一常数，在确定额定动载荷时，取S=0.9。

对点接触，式（2-177）可写为

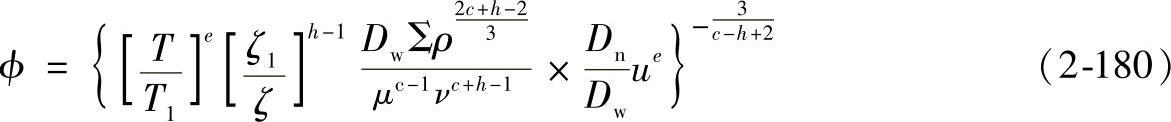
式中，T₁、ζ₁分别为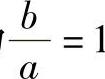时的T、ζ之值；A₁为常数。

把L=1（百万转）时的滚动体载荷称为额定滚动体载荷，并用Q_c表示，则由式（2-179）可得

由式（2-179）和式（2-181）可得点接触时，滚动体载荷与轴承寿命的关系为

对线接触，式（2-178）可改写为

当取L=1时可得额定滚动体载荷为

式中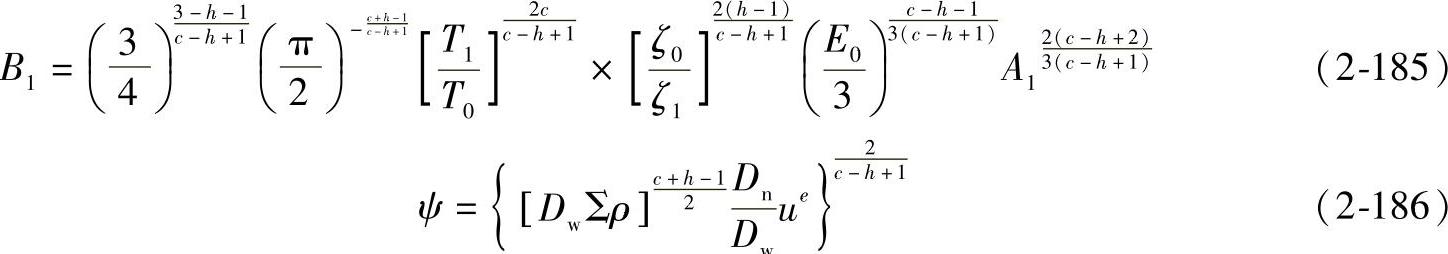

由式（2-183）和式（2-184）可得

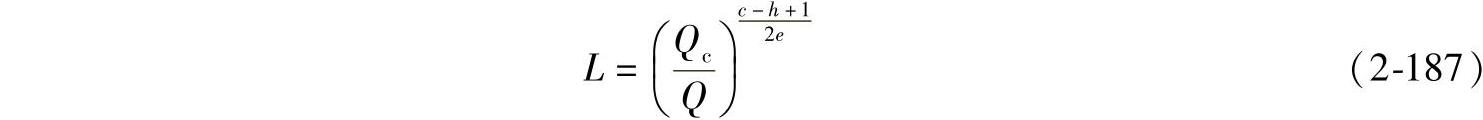
把式（2-182）和式（2-187）写为统一形式，可得

对点接触：

对线接触：

（3）寿命计算公式中指数的确定 寿命计算公式（2-188）中的指数是由大量试验决定的。

1）韦布尔分布斜率e。e表示材料的强度离散特性，因此对于用相同材料制造的不同类型的轴承，e值应大体相同。通过大量的轴承试验统计得出e的数值在1.1左右。为了推导公式方便起见，一般对点接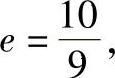触取对线接触取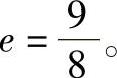

2）滚动体直径D_w的指数。为了决定D_w的指数，用1500套D_w=1.5～25mm范围内的球轴承进行试验，得出D_w的指数为1.8，即在式（2-179）中，D_w的指数为

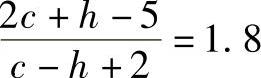
3）寿命指数ε。大量的球轴承的寿命试验证明，对球轴承可取ε=3；用180套线接触的双列球面滚子轴承进行试验，证实对线接触可取ε=4。

4）由已知的e、ε和D_w的指数，可计算出其他指数值，列于表2-16中。

将表2-16的各指数值代入式（2-180）、式（2-181）、式（2-184）～式（2-186）中可得

表2-16 指数值

对点接触：Q_c=A₁φD_w^1.8 （2-191）

对线接触：

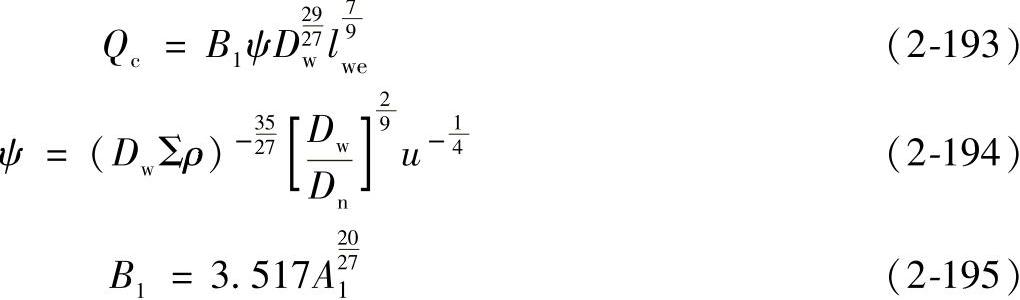
（4）额定滚动体载荷Q_c引入与接触面形状有关的函数F（ρ）

图2-40和图2-41为球轴承和球面滚子轴承曲率半径的表示方法，其中：

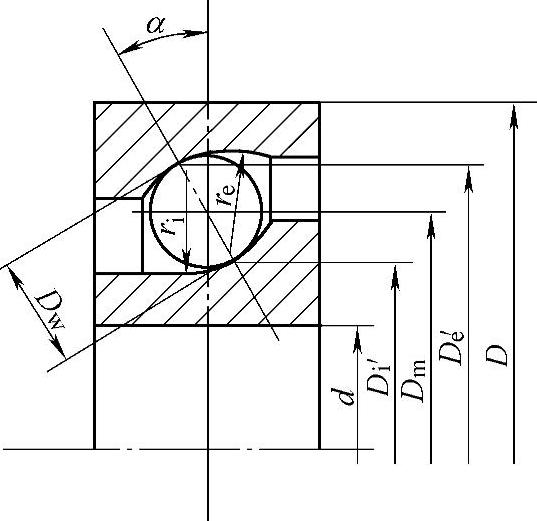
图2-40 球轴承

图2-41 球面滚子轴承

滚道直径和滚动体中心圆直径之间的关系为

D_n=D_i=D_PW-D_Wcosα （2-16）

D_n=D_e=D_PW+D_Wcosα （2-15）

由此可得

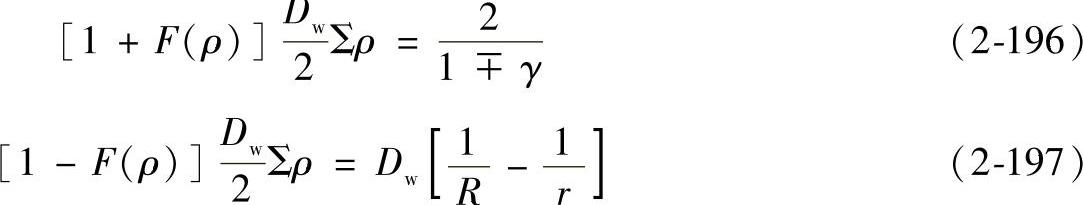
轴承中内、外圈滚动接触次数为

将式（2-196）和式（2-197）、式（2-147）、式（2-148）代入式（2-192）和式（2-194）中可得

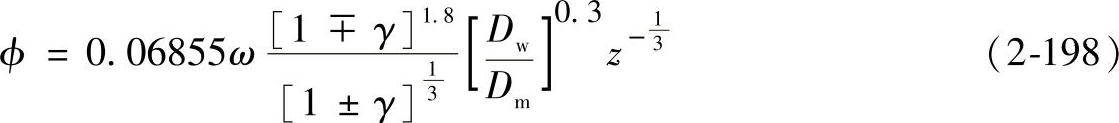
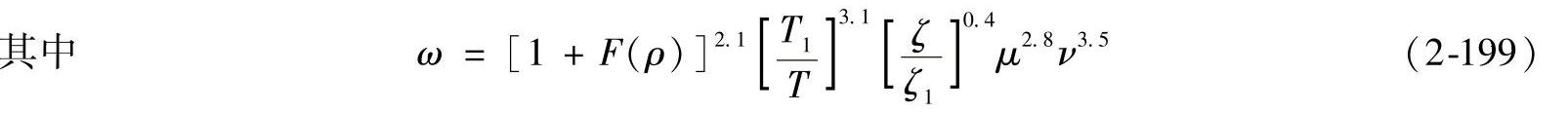
因为线接触时F（ρ）=1，所以

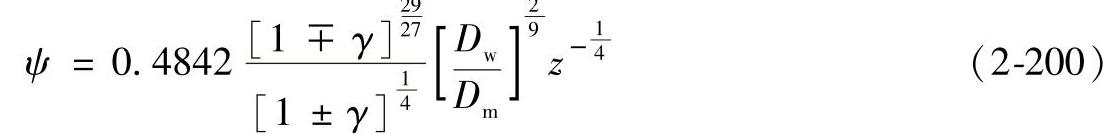
引入函数：

根据Lundberg和Palmgren的假设，再引入

f=1.3Ω^-0.41

如图2-42所示，则

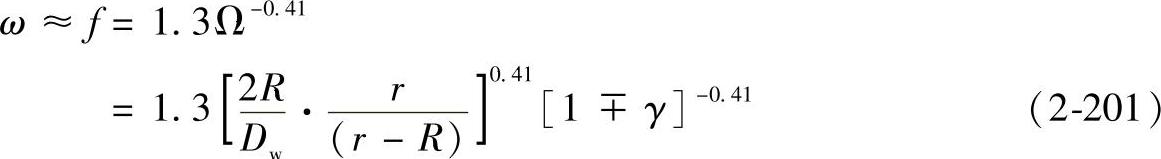
将式（2-198）、式（2-200）和式（2-201）代入式（2-191）、式（2-193）中可得额定滚动体载荷的计算公式为

对点接触：

对线接触：

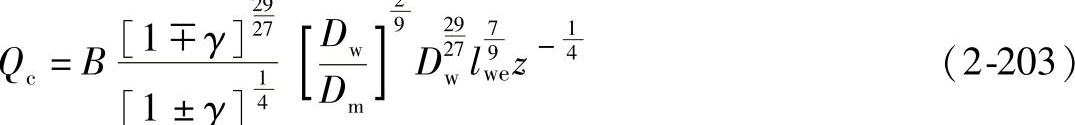
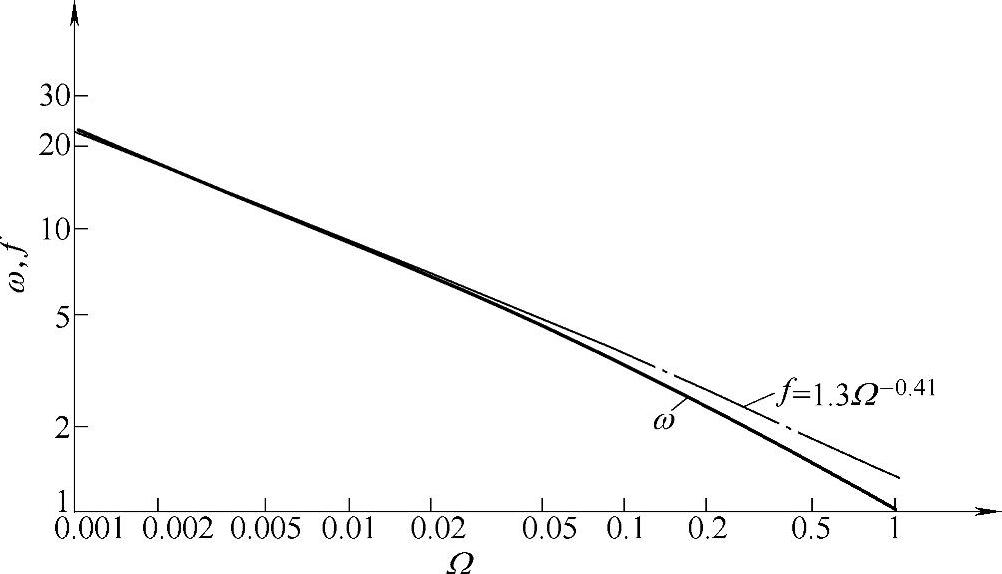
图2-42 函数ω与Ω的关系图

以上各式，上面的符号适用于内圈，下面的符号适用于外圈。

对于用轴承钢制造的，硬度符合标准规定的轴承，由大量实验得出：

A=98 B=551

（5）平均滚动体载荷Q_i、Q_e只有在中心轴向载荷的作用下，轴承中各滚动体才承受相同的载荷。在径向载荷或径、轴向载荷同时作用时，轴承中各滚动体所承受的载荷是不相同的。因此在确定额定滚动体载荷时必须引入“平均”载荷的概念。

为了推导方便，假定：内圈旋转、外圈静止。

根据载荷分布理论，在轴承中滚动体载荷与滚动体所处的位置有关，即

对点接触：

对线接触： t=1.1

当内圈旋转时，内圈各点都经过载荷区，承受相同的变动载荷。按照疲劳累积损伤原理，内圈的平均滚动体载荷，对点接触应为立方平均值，对线接触应为4次方的平均值。

用Q_i表示内圈平均滚动体载荷，则

点接触 s=3

线接触 s=4

将式（2-77）代入式（2-204）中可得

对点接触：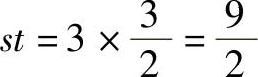

对线接触： st=4×1.1=4.4

当内圈旋转、外圈静止时，外圈滚道各点承受不变的载荷，但其数值与各点所处的圆周位置有关。整个外圈的使用概率等于外圈各部分使用概率的乘积。

对于给定的轴承来说，在式（2-177）和式（2-178）中变量只有Q和L，因此式（2-177）和式（2-178）可写为

对点接触：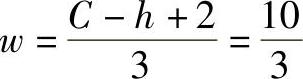

对线接触：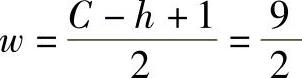

式（2-207）对外圈每一部分都适用，因此对整个外圈来说，有

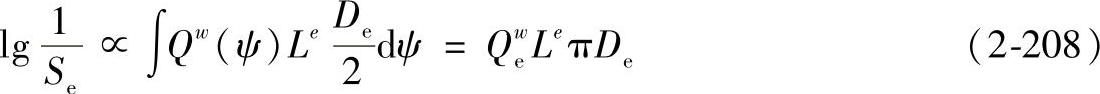
式中 S_e——整个外圈的使用概率；

Q_e——外圈平均滚动体载荷。

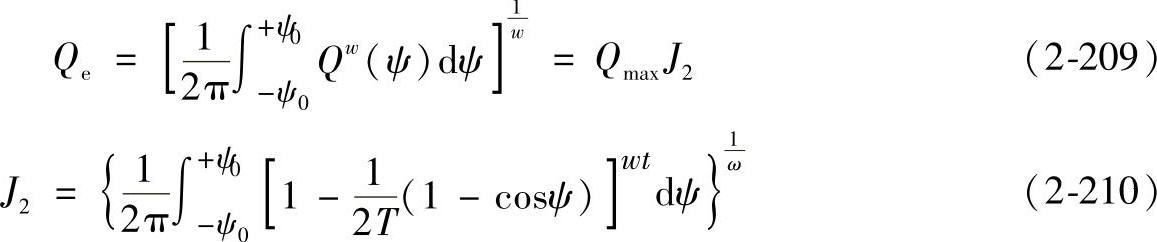
对点接触：

对线接触：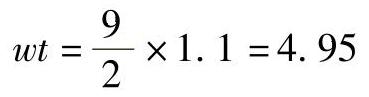

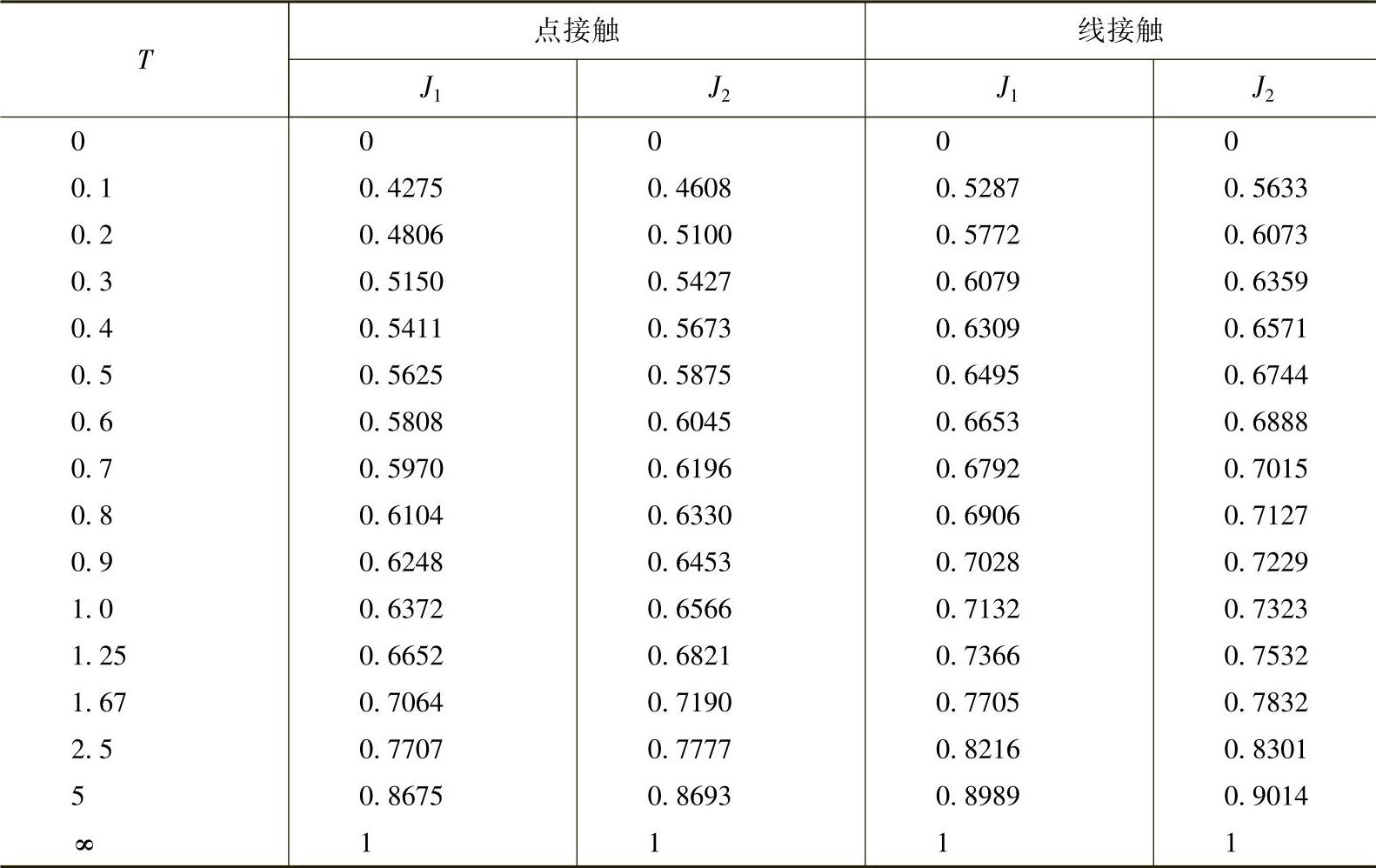
由式（2-206）和式（2-210）可知，J₁、J₂是载荷分布参数T的函数，其数值列于表2-17中。

表2-17所列之值是用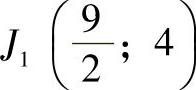代替J₁（4.4；4），用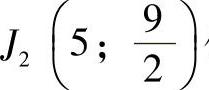代替J₂计算出来的，其误差甚小，可略去不计。

角标1表示旋转套圈，角标2表示静止套圈。

由载荷分布理论可得

将式（2-84）代入式（2-205）和式（2-209）中可得

表2-17 单列轴承的J₁、J₂

6.3.2 决定轴承额定动载荷的方法

（1）定义 轴承的额定动载荷是在假定的运转条件下确定的轴承承载能力，这些假定条件是：

1）内圈相对于载荷向量旋转，外圈相对于载荷向量静止。

2）使用概率S=90%。

3）额定寿命为L=1（百万转）。

4）对向心和向心推力轴承，假定内、外套圈仅有纯径向位移，即轴承内只有半圈滚道承受载荷，载荷分布参数T=0.5。对推力和推力向心轴承，假定内外圈仅有纯轴向位移，即为中心轴向载荷。

由以上假定条件可得额定动载荷C的定义为：一批相同轴承的额定动载荷是在内圈旋转外圈静止的条件下，其中90%的轴承寿命能够达到或超过1百万转时所能承受的载荷。对向心和向心推力轴承，额定动载荷是使滚道半圈受载的载荷的径向分量。对推力和推力向心轴承是中心轴向载荷。

（2）内圈额定载荷C_i，外圈额定载荷C_e轴承中滚动体和内外圈都接触，因此首先由额定滚动体载荷Q_c决定内圈额定载荷C_i和外圈额定载荷C_e，然后由概率乘积定律计算轴承的额定动载荷C。

在式（2-211）和式（2-212）中，如果Q_i和Q_e分别代表内、外圈的额定滚动体载荷Q_ci和Q_ce，则式中的F_r相应为内、外圈的额定载荷C_i、C_e，即

由表2-12和2-17中可查出

对点接触：J_r（0.5）=0.2288 J₁（0.5）=0.5625

J₂（0.5）=0.5875

对线接触：J_r（0.5）=0.2453 J₁（0.5）=0.6512

J₂（0.5）=0.6750

（注：此处的J₁（0.5）和J₂（0.5）是由精确计算而得）

将点接触和线接触情况下的J_r（0.5）、J₁（0.5）、J₂（0.5）的数值代入式（2-213）和（2-214）中可得

点接触：C_i=0.407Q_cizcosα （2-215）

C_e=0.389Q_cezcosα （2-216）

线接触：C_i=0.3767Q_cizcosα （2-217）

C_e=0.3634Q_cezcosα （2-218）

（3）轴承额定动载荷C由轴承载荷分布理论可知，轴承中滚动体载荷与径向载荷

F_r成正比，所以式（2-207）可写为

如果用S_i表示内圈的使用概率，S_e表示外圈的使用概率，S表示整个轴承的使用概率，对内圈可得

如取 S_i=0.9 L=1

则 F_r=Ci

所以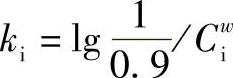

对外圈可得

如取 S_e=0.9 L=1

则 F_r=Ce

所以

对整个轴承来说

S=S_iS_e

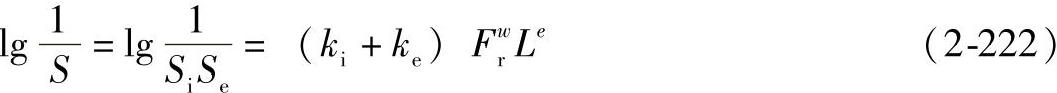
如取 S=0.9 L=1

则 F_r=C

由式（2-220）、式（2-221）、式（2-222）可得

（4）多列轴承的额定动载荷 如果轴承中有i列滚动体，则整个轴承的使用概率是各列使用概率的乘积。用角标1、2、3…i表示轴承中的各列；C₁、C₂、C₃…表示各列的额定动载荷；F_r表示整个轴承承受的径向载荷。如假定各列承受的载荷相同，则各列承受的载荷为，由式（2-219）可得

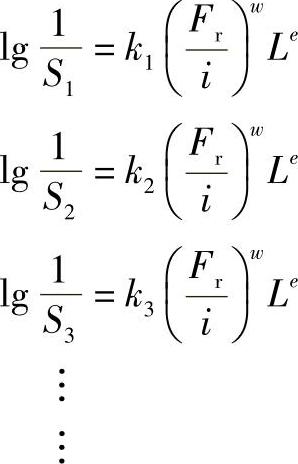
而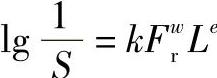

如取 S₁=S₂=S₃=…=S=0.9

L=1

则各上式中的常数可用下列各式计算：

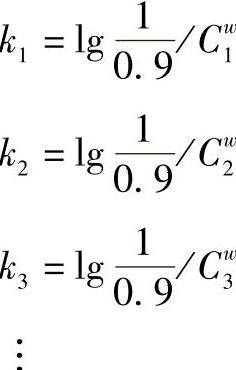
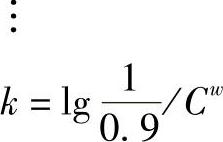
由概率乘积定律可得

S=S₁S₂S₃…S_i

所以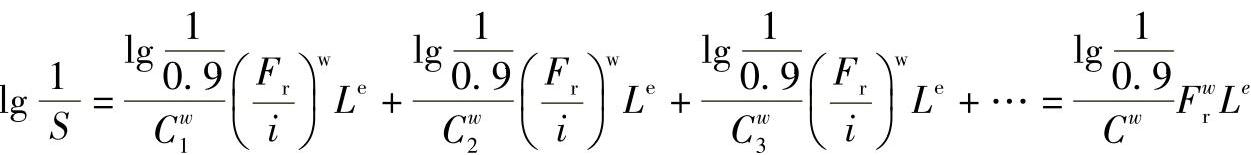

由此可推得

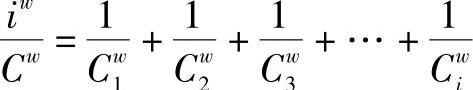
如果轴承中各列的额定动载荷相同，即

C₁=C₂=C₃=…

则可得

对点接触：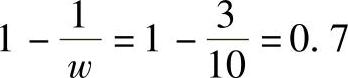

对线接触：

所以双列轴承的额定动载荷并不是单列轴承额定动载荷的两倍，对点接触是2^0.7=1.62倍，对线接触是2^7/9=1.71倍。

由式（2-224）和式（2-226）可得轴承额定动载荷的一般表达式为

6.3.3 球轴承的额定动载荷

上述各节点接触的公式都适用于球轴承。

（1）向心和向心推力球轴承的额定动载荷将式（2-202）、式（2-215）、式（2-216）代入式（2-224）中可得

各种向心球轴承中的应力状态与轴承的结构有关。由于制造误差等因素使轴承的额定动载荷比理论值略低，因此在额定动载荷计算公式中引入一经验系数λ，其数值列于表2-18中。

实验表明，当滚动体直径D_w﹥25.4mm时，额定动载荷不再与D_w^1.8成正比，因此引入经验函数F（D_w）。

当D_w≤25.4mm时F（D_w）=D_w^1.8

当D_w﹥25.4mm时F（D_w）=3.647D_w^1.4

将λ和F（D_w）代入向心球轴承额定动载荷计算公式可得：

表2-18球轴承的系数λ

式中

对向心和向心推力球轴承，当f_i﹤0.52，f_e﹤0.53时，由于摩擦增大，轴承载荷能力并不能增加。因此当f_i≤0.52，f_e≤0.53时应取f_i=0.52，f_e=0.53代入上列各式中。如果f_i﹥0.52，f_e﹥0.53则轴承额定动载荷将有所降低，在计算中应将r_imax、r_emax、D_wmin代入式中。

向心和向心推力球轴承的f_c值可由表2-19中查出。表2-19中的f_c适用于：

对向心和向心推力球轴承：

f_i≤0.52，f_e≤0.53

对调心型球面球轴承：

f_i≤0.53

（2）推力和推力向心球轴承的额定动载荷 承受中心轴向载荷的轴承中，各滚动体承受相同的载荷，根据力的平衡可得：

F_a=Qzsinα （2-230）

在式（2-230）中，如果Q代表额定滚动体载荷Q_c，则F_a即代表内、外圈的额定载荷C_i、C_e。

即 C_i=Q_cizsinα（2-231）

C_e=Q_cezsinα（2-232）

另外 C=g_cC_i （2-224）

将式（2-202）代入式（2-231）、式（2-232）、式（2-224）中，并对α=90°时，引入

表2-19 向心和向心推力球轴承的f_c

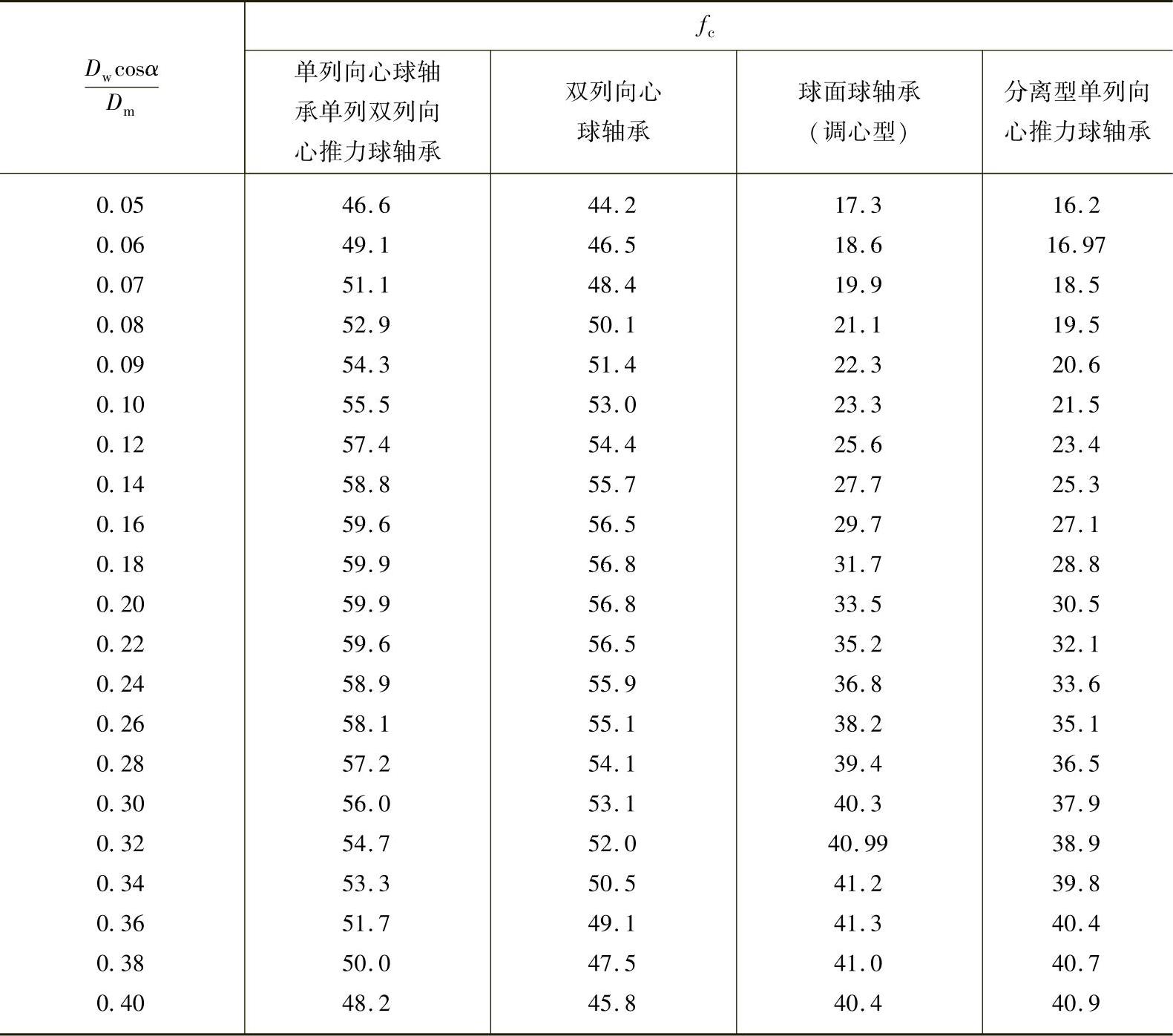
注：1.D_m为钢球中心圆直径；

对表中未给出的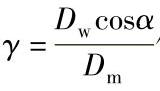值，可用线性插入法求出f_c值。

2.当计算成对安装的两个相同的单列向心球轴承的额定动载荷时，可以作为双列向心球轴承考虑。当计算背对背配置（外圈宽端面相对）或面对面配置（外圈窄端面相对）安装的两个相同的单列向心推力球轴承的额定动载荷时，可以作为一个双列向心推力球轴承来考虑。当计算串联配置（外圈宽窄端面相对）安装的两个或多个相同的单列向心推力球轴承的额定动载荷时，如果这组轴承经过精确制造和仔细安装，使其载荷均等分布，则其额定动载荷为轴承个数的0.7次方乘以一个单列向心推力球轴承的额定动载荷值。

1）当α=90°时

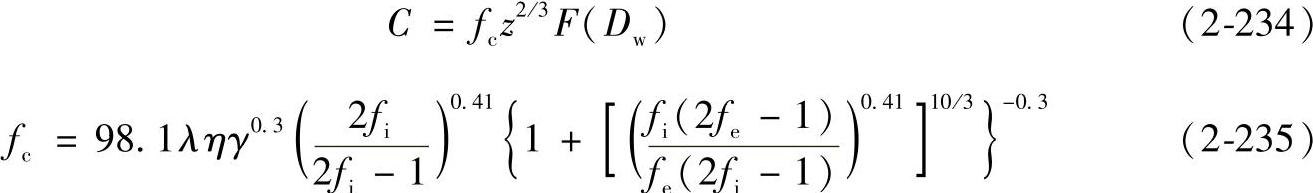
2）当α≠90°时

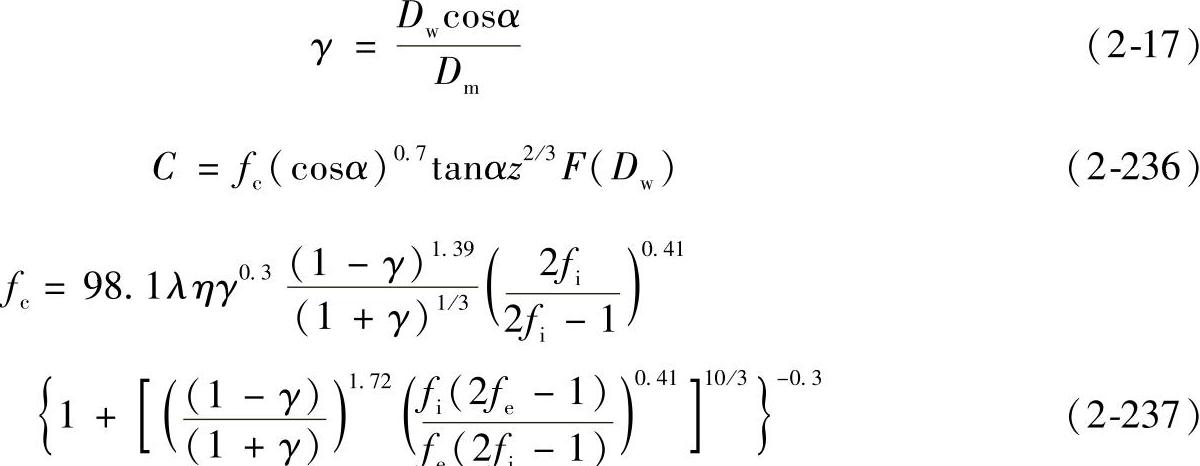
在式（2-234）和式（2-236）中

当D_w≤25.4mm时F（D_w）=D_w^1.8

D_w﹥25.4mm时F（D_w）=3.647D_w^1.4

在式（2-235）和式（2-237）中，λ的数值可由表2-18中查出。

在推力轴承中由于制造误差，如滚道壁厚差等，使轴承中载荷分布不均匀，因而使轴承的实际载荷能力比理论计算的额定动载荷低。一般是在f_c的计算式中，引入两个经验系数λ和η。降低系数η的数值与接触角有关，有

对球轴承：

对滚子轴承：

η=1-0.15sinα （2-239）

（3）对于单向承受轴向载荷且钢球直径相同的双列或多列推力球轴承，其额定动载荷可由概率乘积定律求出。

如用C₁、C₂、C₃…C_n分别表示各列的额定动载荷值，z₁、z₂、z₃…z_n表示各列的滚动体数，C表示整个轴承的额定动载荷，则

z=z₁+z₂+z₃+…+z_n

由式（2-219）可得

而

如取

S₁=S₂=…=S=0.9

L=1

则可得

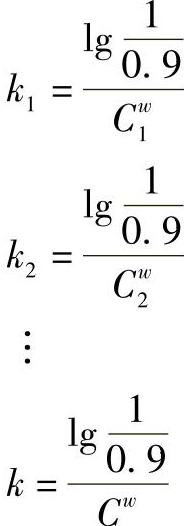
根据概率乘积定律可得

S=S₁S₂…S_n

将k₁、k₂……k值代入即可得

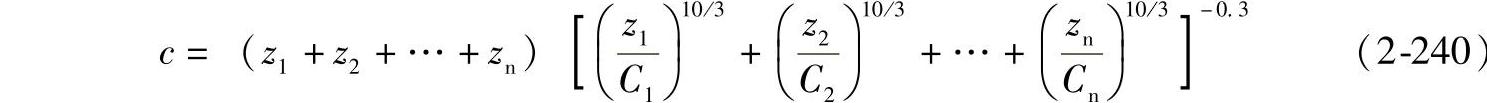
推力轴承的系数f_c值列于表2-20中。

表2-20 推力球轴承的系数f_c

表2-20所列之值适用于f_i=f_e≤0.54的推力球轴承。

如果沟曲率半径大于0.54D_w，应由式（2-235）或式（2-237）计算f_c值。

6.3.4 滚子轴承的额定动载荷

（1）线接触滚子轴承的额定动载荷理论计算公式 滚子轴承的接触形式很多，在确定其额定动载荷时既要考虑接触形式的影响，又要考虑制造、安装误差的影响。

对滚动体与两套圈滚道均为线接触的滚子轴承，其额定动载荷的理论计算公式可由下述方法确定。

向心滚子轴承：

将式（2-203）代入式（2-217）和式（2-218）中计算出C_i和C_e，然后由式（2-224）可得

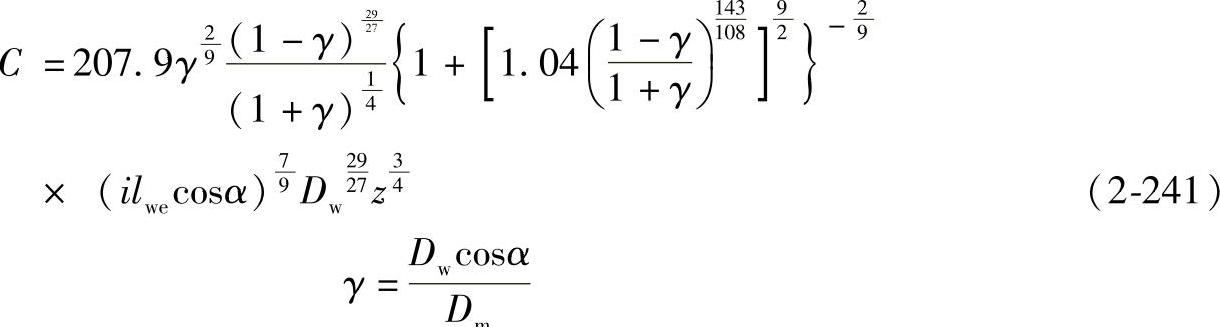
推力滚子轴承：

在中心轴向载荷的作用下，轴承中各滚动体承受相同的载荷，根据力的平衡条件可得

F_a=zQsinα

如果上式中Q代表额定滚动体载荷Q_c，则F_a即为内、外圈的额定载荷C_i、C_e，且

C_i=zQ_cisinα （2-231）

C_e=zQ_cesinα （2-232）

将式（2-203）代入式（2-231）、式（2-232）、式（2-224）中可得

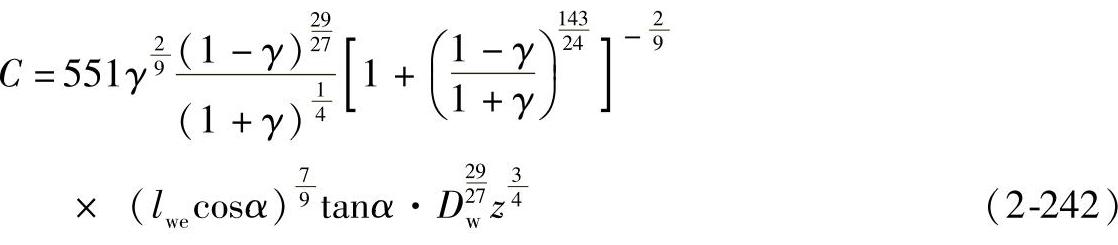
对于α=90°的推力滚子轴承，如将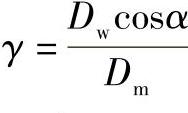代入式（2-242）中，而且因为

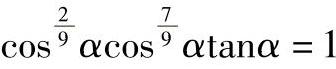
所以α=90°的推力滚子轴承的额定动载荷计算式为

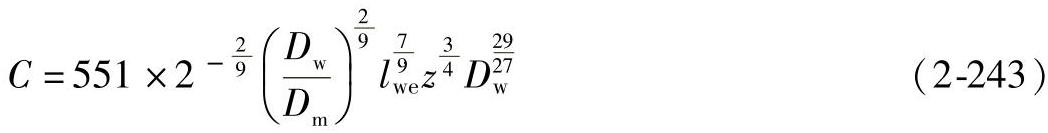
（2）滚子轴承的接触类型 滚子和滚道的母线为直线时，称为线接触。当滚子的母线为曲线（带凸度的滚子），或滚道的母线为曲线（带凸度的滚道）时，滚子与滚道的接触类型与滚动体载荷有关。对于给定的凸度值，对应有一个最佳滚动体载荷，即在此载荷的作用下，载荷沿滚动体长度方向均匀分布，不产生边缘应力。如实际滚动体载荷大于该凸度值相应的最佳滚动体载荷，则将产生边缘应力，使轴承寿命降低。如果实际滚动体载荷小于最佳滚动体载荷，则不发生边缘应力，但滚子在长度方向将有一部分不承受载荷，因而没有完全利用轴承的载荷能力。

由轴承的载荷分布理论可知：在向心轴承中，滚动体载荷与滚动体所处的圆周位置有关。因此对某一给定的凸度值来说，在轴承一转中，滚动体与滚道的接触类型也可能是不同的。在同一轴承中，滚动体与内、外圈滚道的接触类型也可能是不同的。

对某一确定的应用场合来说，滚子轴承的最佳设计方案是在给定的载荷作用下，使承受最大滚动体载荷的滚子与滚道接触处不产生边缘应力。对于通用轴承来说，首先假定作用于轴承上的载荷与额定动载荷的比值，然后确定其凸度值。

一般，滚子与滚道的接触类型可按接触椭圆长轴与滚子有效接触长轴的关系来确定。

1）线接触。线接触是指当不承受载荷、安装同心度良好时，滚子和滚道沿它们的母线全长接触。或者在载荷作用下，其接触椭圆长轴2a﹥1.5l_we的情况（l_we为滚子有效接触长度）。

2）点接触。点接触是指当不承受载荷、安装同心度良好时，滚道和滚子中部一点接触。或者当承受载荷时，承受最大滚动体载荷的滚子与滚道接触处的接触椭圆长轴小于滚子有效接触长度，即2a﹤l_we。

3）修正线接触。修正线接触是指修改滚子或滚道两端部母线的形状，使承受最大滚动体载荷的滚子端部的接触应力，接近于其余部分的接触应力，或其接触椭圆长轴在l_we﹤2a﹤1.5l_we的范围内。

滚子轴承中可能出现的几种接触类型和相应的条件列于表2-21中。

表2-21 滚子轴承的接触类型

（3）降低系数λ、η大量的实验数据表明，滚子轴承的实际承载能力比理论计算的额定动载荷低，因此在理论计算公式中引入一降低系数λ。降低系数λ的数值与轴承结构形式、滚子引导方式、接触类型等许多因素有关。各种轴承的λ值，列于表2-22中。

在推力滚子轴承中，由于制造误差和安装误差等原因还需要引入降低系数η。

η=1-0.15sinα （2-239）

（4）修正系数ν由表2-16中可知，式（2-188）中的寿命指数，点接触时ε=3，线接触时ε=4。

表2-22 λ、ν的数值

①ISO/R281原规定的数值与λν=0.73相对应，1971年TC₄决定提高到与λν=0.83相应的数值。

②ISO/R281只规定滚子轴承的

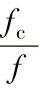值，但Palmgren在1964年版本中对球面滚子轴承的数值单独给出。

滚子轴承的结构形式很多，接触类型比较复杂，有线接触的也有点接触的。在同一轴承中滚动体可与一套圈为点接触，而与另一套圈为线接触。对同一套圈而言，在不同载荷范围内可以由点接触转变为线接触。显然，对滚子轴承来说寿命指数ε在3～4之间变化。

为了简化滚子轴承的寿命计算，对滚子轴承的寿命指数统一取为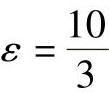，而在线接触滚子轴承额定动载荷理论计算式（2-241）和式（2-242）中引入修正系数ν。即如用C_l表示式（2-241）和式（2-242）中的线接触滚子轴承额定动载荷的理论计算值，则对所有接触类型的滚子轴承的额定动载荷的理论值可用下式表示：

C=νC_l （2-244）

确定修正系数ν时，应使轴承在常用的寿命范围内，即在100（百万转）﹤L﹤10000（百万转）的范围内误差最小。

在式（2-188）中，Q_c与额定动载荷C成正比关系，因而在相同的轴承载荷作用下，可得

式中P为轴承当量动载荷，见本章第4节。

对于滚子与两套圈滚道均为线接触的情况，寿命指数应为4，则上式可写为

如将寿命指数改为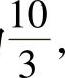则可得

由式（2-244）、式（2-245）、式（2-246）可得

如取 L=500百万转

则可得：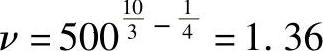

如果滚动体与两个滚道都为点接触，则在一定的载荷作用下，将由点接触转变为线接触。假定在L=100百万转时，两个套圈同时发生转变，则寿命指数ε将由3转变为4。如用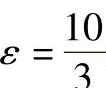来代替将有5%的误差，由式（2-247）可得

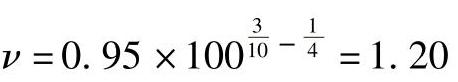
如果滚动体与一套圈为点接触，与另一套圈为线接触。假定点接触的套圈在L=100百万转时发生点接触向线接触的转变，则这种情况下由式（2-247）可得

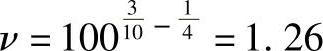
各种情况下的ν值列于表2-22中。

（5）滚子轴承额定动载荷计算公式 如将λ、η、ν引入线接触滚子轴承额定动载荷理论计算式中，则可得滚子轴承额定动载荷的一般计算公式。

向心滚子轴承：

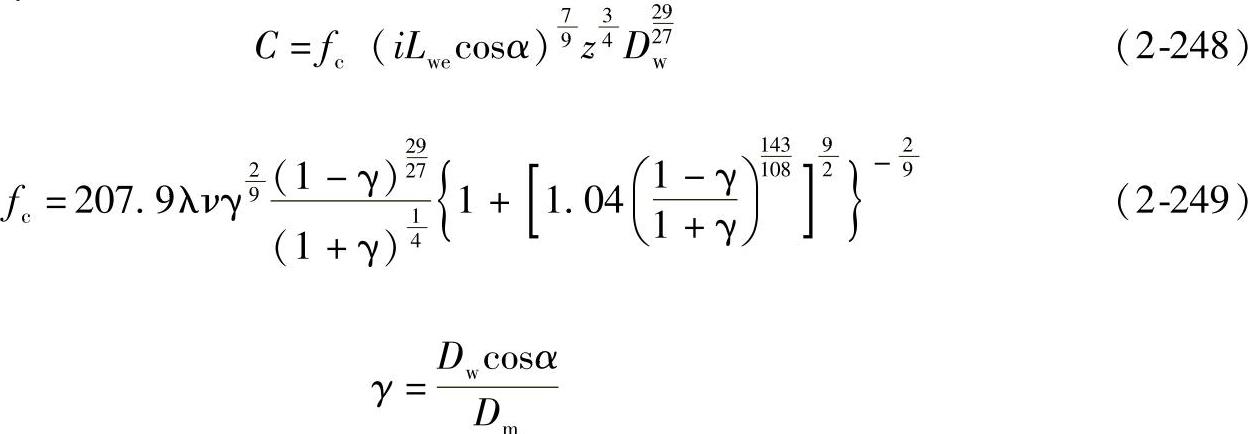
推力向心滚子轴承：α≠90°

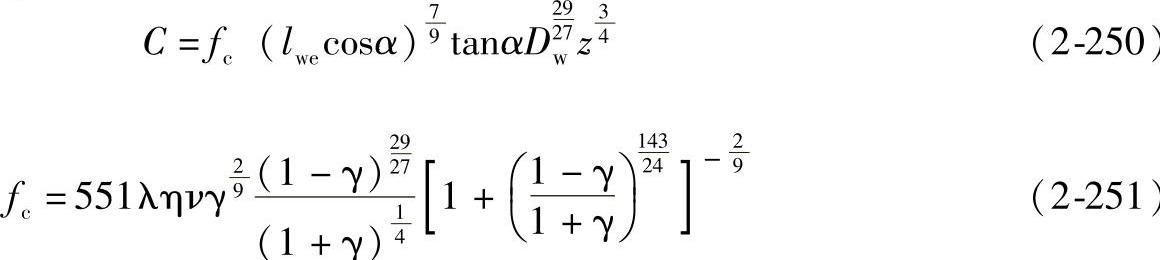
推力滚子轴承：α=90°

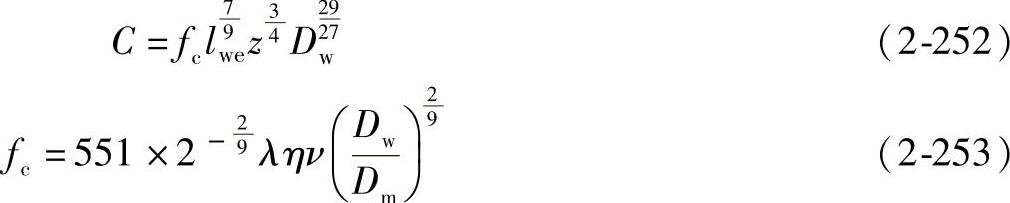
多列单向推力滚子轴承：

对于单向承受轴向载荷的双列和多列推力滚子轴承，可用与式（2-240）相同的推导过程，求得额定动载荷的计算公式。

如果z₁、z₂、z₃、…、z_n为各列的滚动体数：l_we1、l_we2、l_we3、…、l_wen为各列滚动体的有效接触长度；C₁、C₂、…、C_n为各列的额定动载荷。则整个推力轴承的额定动载荷可由下式计算：

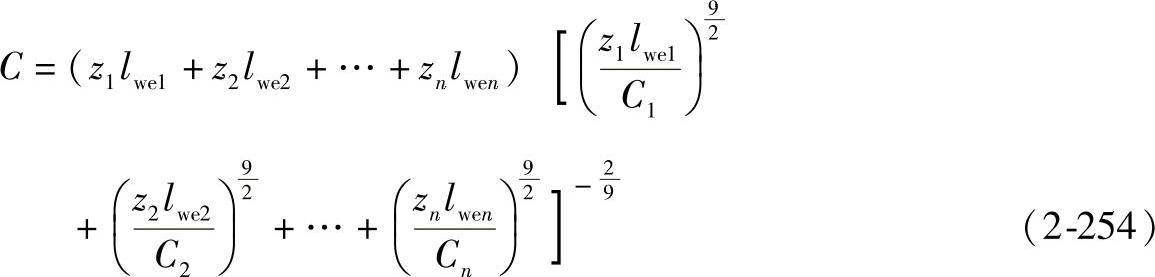
向心滚子轴承和推力滚子轴承的f_c值列于表2-23和表2-24中。

表2-23 向心滚子轴承的f_c

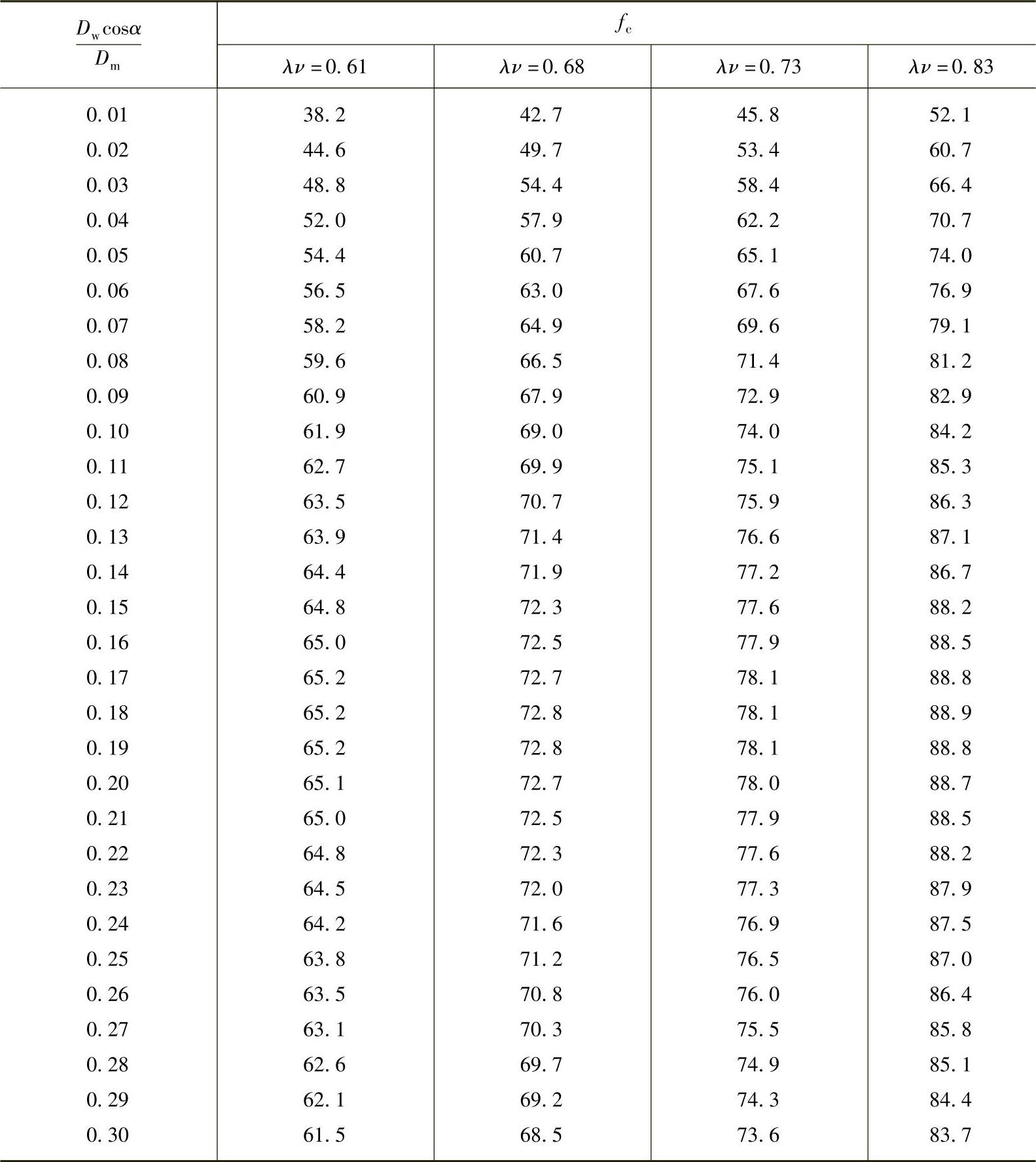
表2 - 24 推力滚子轴承的fc

① 适用于45°﹤α﹤60°。

② 适用于60°﹤α﹤75°。

③ 适用于75°﹤α﹤90°。

表中未列之值可用线性插入法求得。

表列之值是相应于取λν=0.73的数值，在ISO/R281中推荐的数值相应为λν=0.68，后来于1971年决定提高至此表所列数值。

表2-23中λν=0.83栏的f_c值适用于：

1）滚子与两套圈滚道均为修正线接触的短圆柱滚子轴承，滚子由保持器精确引导，并由任一套圈的两个挡边对其端面精确引导。

2）滚子与两套圈滚道均为修正线接触的圆锥滚子轴承，其滚子由一挡边精确引导。

3）对称球面滚子与两套圈滚道均为修正线接触的向心球面滚子轴承，其对称球面滚子由轴向浮动挡圈精确引导。

与上述情况不同的向心滚子轴承，可由表2-22查出λν值，再由式（2-251）计算出f_c值。或由表2-23中查出相应的f_c值。

ISO281/I—1977标准中建议对短圆柱滚子轴承、圆锥滚子轴承、球面滚子轴承取统一的f_c值，因此表2-23所列的λν=0.83之值，可以认为是这三类轴承的最大值。

表2-24所列的值是最大值，仅适用于在轴承载荷作用下，最大载荷滚子与滚道接触处应力均匀分布的情况。如果在载荷作用下，滚子与滚道接触的某些部分存在应力集中的情况，则应取比表列较低的数值。例如，存在边缘应力的滚子轴承；滚子没有精确引导的轴承，滚子长度大于滚子直径2.5倍的轴承；滚子过长引起较大滑动的轴承都应取比表列较低的数值。

各类轴承f_c的计算公式列于表2-25中。

表2-25 滚动轴承额定动载荷计算公式表

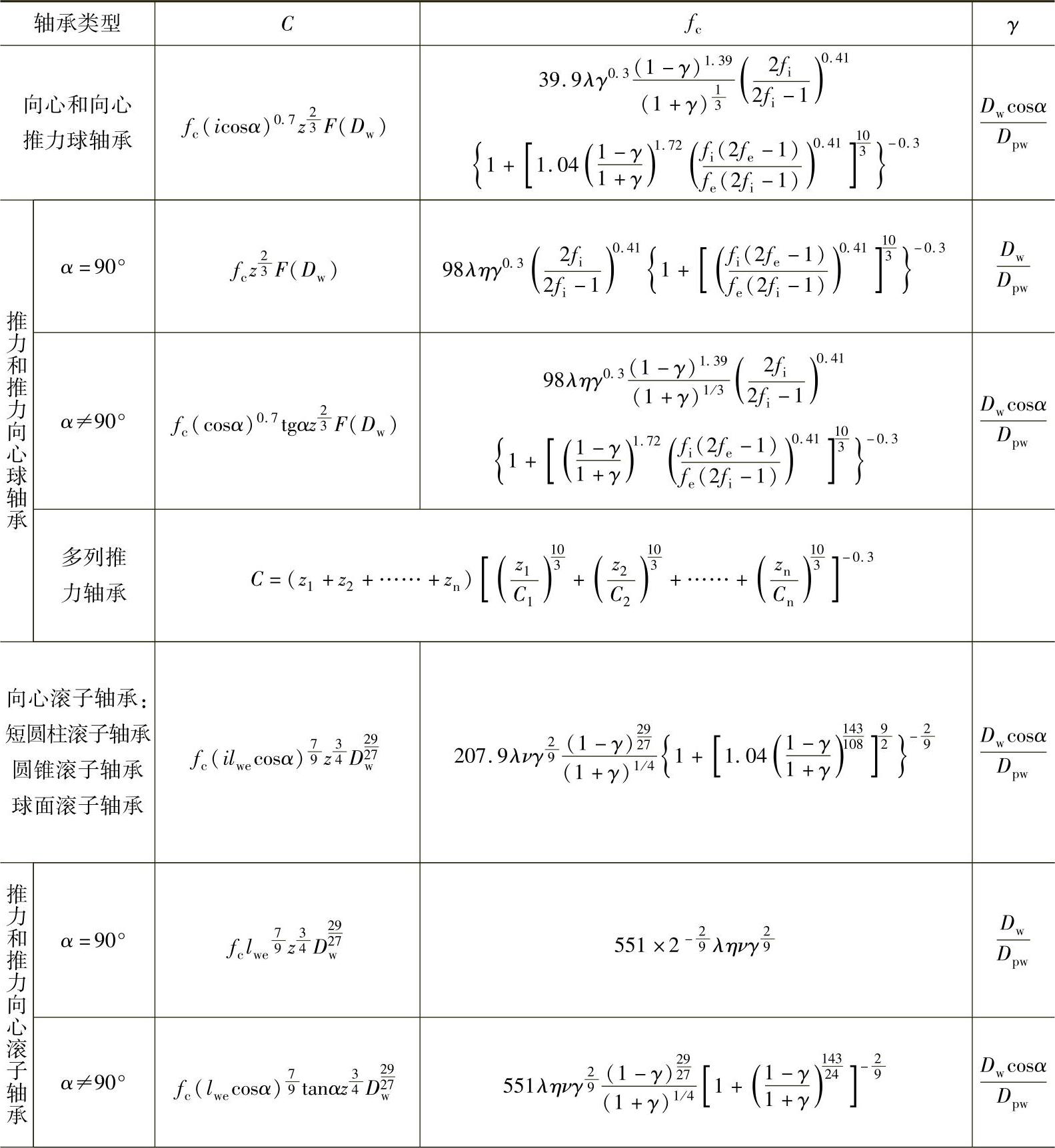
（续）

注：1.当D_w≤25.4mm F（D_w）=D_w^1.8

当D_w﹥25.4mm F（D_w）=3.647D^1.4

2.对球轴承

对滚子轴承η=1-0.15sinα

3.λ、ν的数值可由表2-18和2-22查出

表中所用符号：

C——轴承额定动载荷（kN）

α——接触角

z——一列轴承中滚动体数

i——滚动体列数

D_w——滚动体直径（mm）

l_we——有效接触长度（mm）