首页理论教育滚动轴承疲劳寿命的基本规律与优化方法

滚动轴承疲劳寿命的基本规律与优化方法

2023-06-26 理论教育版权反馈

【摘要】：纵坐标表示每套轴承的实际寿命，横坐标表示按寿命长短排列的轴承序号。针对轴承疲劳寿命相当离散的特征，为表征一批轴承的寿命，必须用数理统计方法计算在一定使用概率下的寿命。式2-166叫作滚动轴承疲劳寿命的韦布尔分布。滚动轴承额定动载荷的理论，是建立在轴承寿命符合韦布尔分布的基础上。

6.2.1 疲劳寿命的基本规律

大量的轴承寿命试验数据证明，滚动轴承的疲劳寿命是相当离散的。一批结构尺寸、材料、热处理、加工方法相同的轴承在相同的使用条件下，其寿命相差很大，最低寿命和最高寿命可以相差几十倍甚至上百倍。图2-37是一组20套轴承的寿命试验结果。纵坐标表示每套轴承的实际寿命，横坐标表示按寿命长短排列的轴承序号。由图中可明显看出，最高寿命和最低寿命相差是很大的。

从大量的轴承寿命试验结果来看，绝大多数的试验都有如图2-37所示的趋势。因此，可将轴承寿命离散情况用图2-38所示的一般规律表示。

图2-38中横坐标表示能达到或超过寿命L_s的轴承相对数量S，纵坐标表示与S相对应的轴承寿命L_s（以90%轴承能达到或超过的额定寿命L作为1表示的寿命）。

由图2-38可看出：

1）一批数量相当多的轴承，100%能够达到的寿命为零（对有限数量的轴承来说有一最低寿命L₀存在）。

2）能够达到无限长寿命的轴承相对数量为零，即没有任何一个轴承可以无限期的运转下去。

针对轴承疲劳寿命相当离散的特征，为表征一批轴承的寿命，必须用数理统计方法计算在一定使用概率下的寿命。一般是从图2-38中取两个特殊点的寿命来表征一组轴承的寿命。即额定寿命和中值寿命。

有关轴承寿命的名词定义是：

1）一个轴承的寿命：是指一个轴承中，任一滚动体或任一滚道出现疲劳剥落前运转的总转数，或在一定转速下的工作小时数。

2）额定寿命L：一批相同轴承的额定寿命，是指其中90%的轴承在疲劳剥落前能够达到或超过的总转数，或在一定转速下的工作小时数。

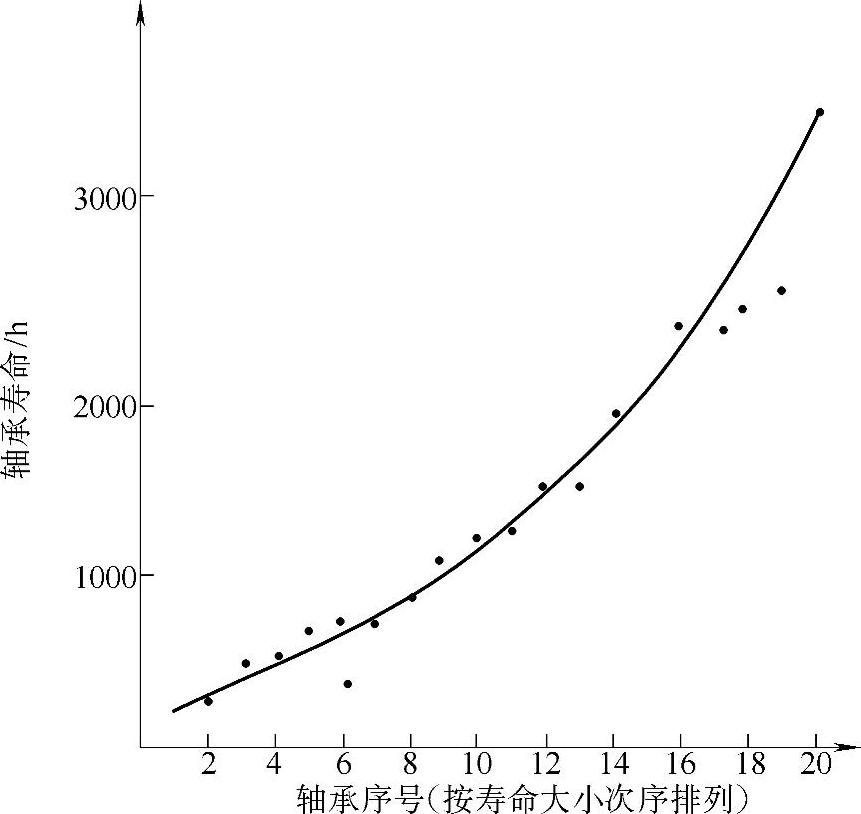
图2-37 轴承疲劳寿命试验结果

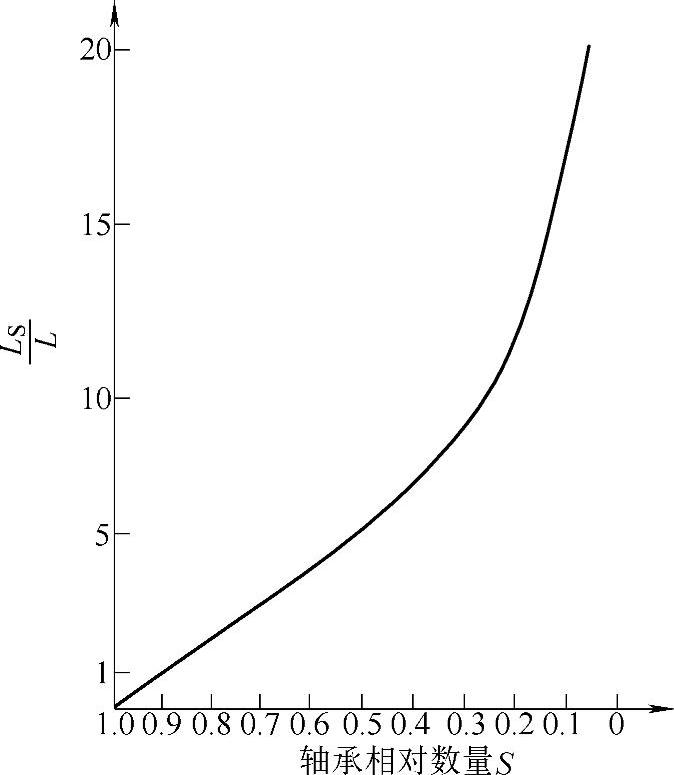
图2-38 轴承疲劳寿命的一般规律

3）中值寿命L_m：一批相同轴承的中值寿命，是指其中50%的轴承在疲劳剥落前能够达到或超过的总转数，或在一定转速下的工作小时数。中值寿命L_m不是一批轴承寿命的数学平均值。

一般中值寿命L_m是额定寿命的五倍左右。

4）使用概率S：是指一批相同的轴承，能够达到或超过寿命L_s的轴承相对数量。

式中 N_S——达到或超过L_s的轴承数量；

N——试验轴承的总数。

对于一个轴承来说，使用概率S可看作是该轴承能够达到或超过L_s的概率。或叫做使用可靠性（可靠度）。

5）破坏概率F：是指一批相同轴承中，未达到L_s寿命而疲劳破坏的轴承相对数量。

在选用轴承时，主要是计算在给定工作条件下的额定寿命。一般取S=0.9的寿命作为额定寿命，对一个轴承来说，达到额定寿命的可靠性为90%。

6.2.2 滚动轴承疲劳寿命的韦布尔分布

图2-38的曲线可看作是一指数曲线，可用下式表示：

如在公式两边取对数，则可得

式中 S——使用概率，即达到或超过L_s寿命的轴承相对数量；

L_s——与S相对应的轴承寿命。习惯上角注用1-S的数值标注，如L₁₀表示使用概率为90%的寿命，L₅表示使用概率为95%的寿命；

e——韦布尔分布斜率；

A——常数。

式2-166叫作滚动轴承疲劳寿命的韦布尔分布。如果在双对数坐标纸上，取纵坐标为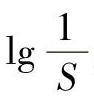，横坐标为L_s，令

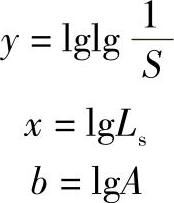
则式（2-166）变为

y=ex+b

显然上式为一直线方程，e为该直线的斜率。所以韦布尔分布式（2-166）在双对数坐标中为一直线。e可由下式计算：

e值表示一批相同轴承寿命离散的程度，e值愈小，表示该批轴承寿命愈离散，因此e也称为离散指数。一般：

对球轴承取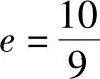

对滚子轴承取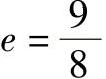

图2-39为两种球轴承韦布尔分布的实例。是瑞典SKF轴承公司的实验结果。

利用式（2-166）可以计算出任意使用概率下的寿命。

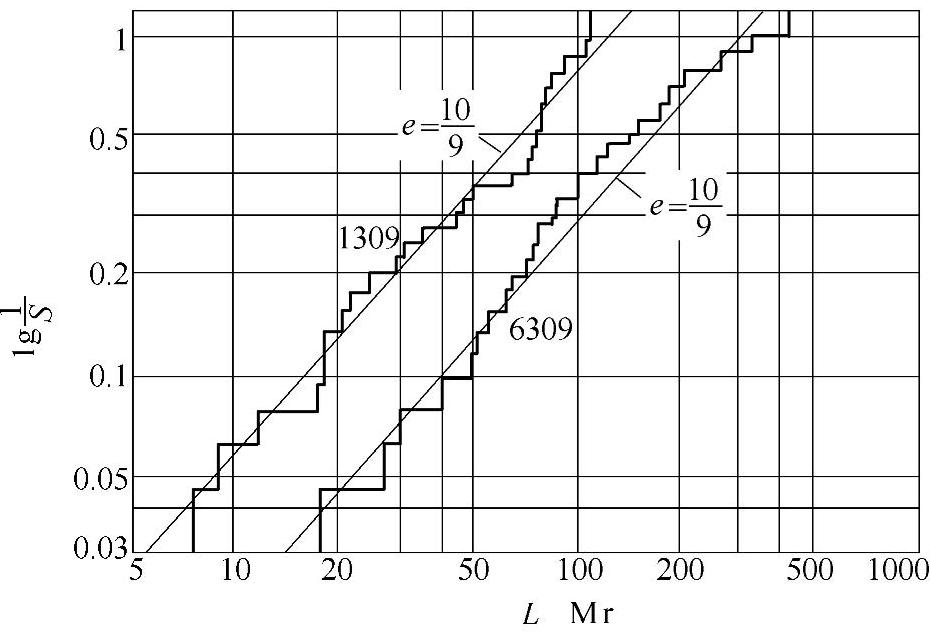
图2-39 滚动轴承疲劳寿命的韦布尔分布

在式（2-166）中如取

S=0.9 则L_s=L

由此可得：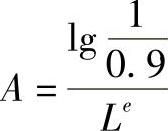

代入式（2-166）中可得

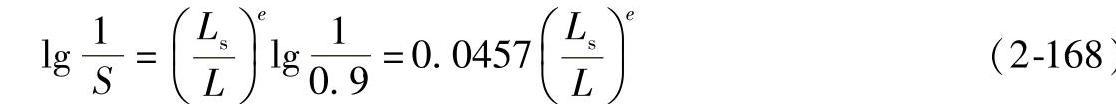
在式（2-168）中如果已知额定寿命L和韦布尔分布斜率e，则很容易计算出任意使用概率下的寿命。

T.Tallian分析了2250套轴承寿命试验数据，证实在0.4﹤S﹤0.93范围内，轴承寿命很好地符合韦布尔分布，因此式（2-168）可在S=0.4到S=0.93的范围内应用。滚动轴承额定动载荷的理论，是建立在轴承寿命符合韦布尔分布的基础上。

式（2-168）可有下列两种用途：

1）一般选用轴承时，是根据滚动轴承样本所列的额定动载荷数据，计算可靠性为90%的寿命，即额定寿命L。如果按照实际需要，对轴承寿命可靠性的要求不是90%，则可用式（2-168）计算任意可靠性要求的轴承寿命（可靠性要求高于93%的轴承寿命计算方法见本章第7节）。

【例10】根据轴承使用条件，6307轴承的额定寿命为6000h，如果可靠性要求为S=0.80，轴承的寿命为多少？

【解】将S=0.80 L=6000 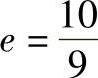代入式（2-168）可得

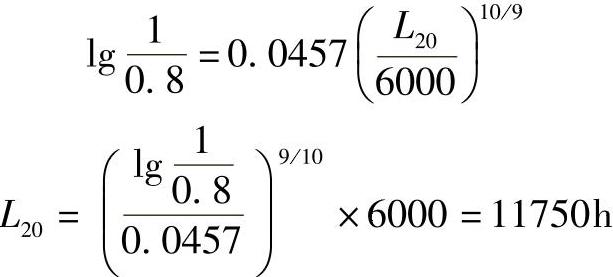
2）当许多台同一种机器同时运转时，根据在运转一定时间后轴承损坏的数量，可以估计剩余轴承的运转时间。

【例11】 100个调心滚子轴承，在给定的使用条件下运转2000h后，有20个轴承已疲劳破坏。估算再运转1000h后可能还有多少个轴承破坏。

【解】 20个轴承疲劳破坏以后，还有80个轴承在继续运转，因而达到2000h寿命的使用概率为

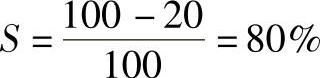
如设再运转1000h后的使用概率为S₁，则

L_s1=（2000+1000）h=3000h

对滚子轴承取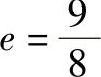

由式（2-168）可得

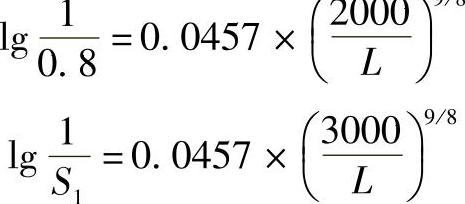
由以上两式可得

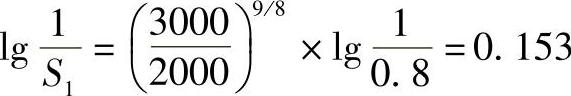
所以S₁=0.70

因此，再运转1000h后还可能再有10个轴承疲劳破坏。

【例12】某车间有一组球轴承在相同的使用条件下运转，其额定寿命为L=1000h。在运转1500h后有些轴承已经破坏，试估算剩余轴承的90%不破坏的话，预计还能再运转多少时间？

【解】假设：在运转L_a=1500h后，未破坏的轴承的相对数量为S_a，则剩余轴承中90%不破坏的相对数量为S_b=0.9S_a，与S_b对应的寿命为L_b

由式（2-168）可得

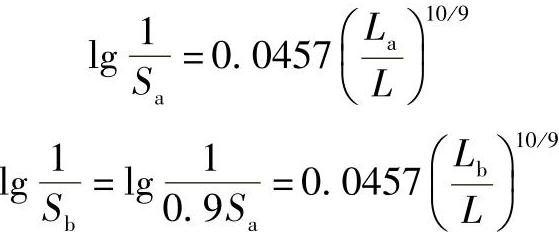
而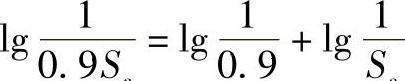

所以由上列两式可得

L_b=（L_a^10/9+L^10/9）^9/10=（1500^10/9+1000^10/9）^9/10h

=2340h

因此，在运转1500h后，剩余轴承的90%还能再运转：2340h-1500h=840h。