角接触球轴承的接触角变化探究

2023-06-26 理论教育版权反馈

【摘要】：向心球轴承和角接触球轴承的接触角是随载荷而变化的，尤其是名义接触角很小时，接触角变化比较显著。图2-34为名义接触角为α0的角接触球轴承，在承受轴向载荷Fa后接触角变化的情况。图2 - 34 角接触球轴承的接触角变化o′i是内、外圈相对移动后，内圈滚道的曲率中心。

向心球轴承和角接触球轴承的接触角是随载荷而变化的，尤其是名义接触角很小时，接触角变化比较显著。

图2-34为名义接触角为α₀的角接触球轴承，在承受轴向载荷F_a后接触角变化的情况。在轴向载荷F_a作用之前，接触角为α₀，在F_a作用之后，内外圈在轴向相对移动了δ_a。

图2-34中，o_i、o_e分别为轴向载荷作用之前，内、外圈滚道的曲率中心。

图2 - 34 角接触球轴承的接触角变化

o′_i是内、外圈相对移动后，内圈滚道的曲率中心。

由几何关系可得

o_io_e=r_i+r_e-D_w=qD_w

o′_io_e=r_i+r_e-D_w+δ_n=qD_w+δ_n

其中，δ_n为钢球与内外圈接触处总的弹性变形量。

由本章第2节可知

δ_n=KQ^2/3

式中，K为常数。如忽略在接触处法向平面内滚道曲率的影响，而且在轴向平面内，内、外圈滚道的沟曲率半径相同，则

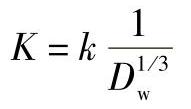
其中，k值可由表2-7或图2-16中查出。

Q为滚动体载荷，在中心轴向载荷F_a的作用下

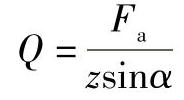
由图2-34的几何关系可得

o_io_ecosα₀=o′_io_ecosα

将上述K、Q的数值代入可得

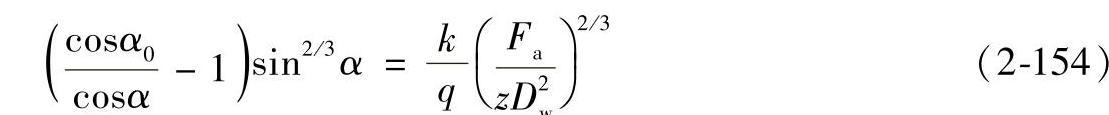
对一定型号的角接触球轴承，如已知F_a，则可由式（2-154）确定实际接触角α的数值。

对于径向游隙G_r=0的向心球轴承，其初始接触角α₀=0，这时，式（2-154）可写为

经三角函数变换，有

利用级数展开式：

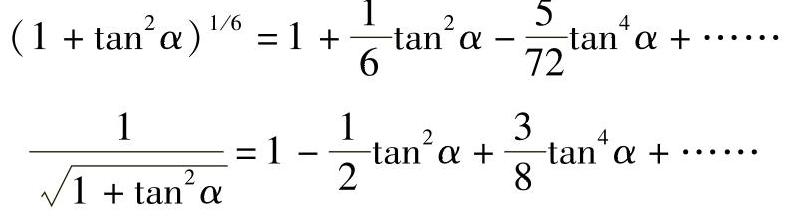
略去高阶微量则可得

同时承受径向载荷和轴向载荷时，角接触球轴承中，接触角随滚动体所处的位置而不同。