首页理论教育单向推力轴承载荷分布优化分析

单向推力轴承载荷分布优化分析

2023-06-26 理论教育版权反馈

【摘要】：单向推力轴承可以承受偏心载荷，如图2-29所示。因此在这种情况下，各滚动体承受的载荷是不相同的。如引入载荷分布参数T，则那么式可改写为将式代入可得图2 - 29 单向推力轴承的载荷分布对球轴承：对滚子轴承：t=1.1由轴承受力平衡可得将式代入，并引入载荷分布积分Ja、JM可得式中由式和式可得在表2-14中列出了与JM、Ja的对应关系。因此单向推力球轴承仅能承受的偏心载荷。

当α=90°的推力轴承承受一中心轴向载荷时，各滚动体承受相同的载荷。

单向推力轴承可以承受偏心载荷，如图2-29所示。偏心载荷可以分解为一个中心轴向载荷F_a和在通过轴承中心线和载荷作用线平面内的力矩M，而

M=eF_a （2-104）

在中心轴向载荷F_a的作用下，轴承轴圈相对座圈轴向移动了δ_a，在力矩M的作用下，两套圈相对转动了θ角。因此在这种情况下，各滚动体承受的载荷是不相同的。

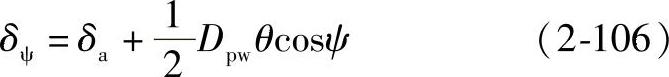
如引入载荷分布参数T，则

那么式（2-106）可改写为

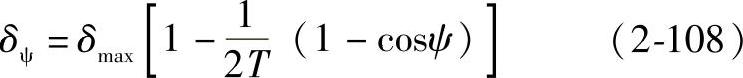
将式（2-58）代入可得

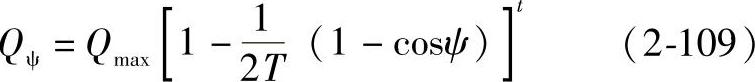
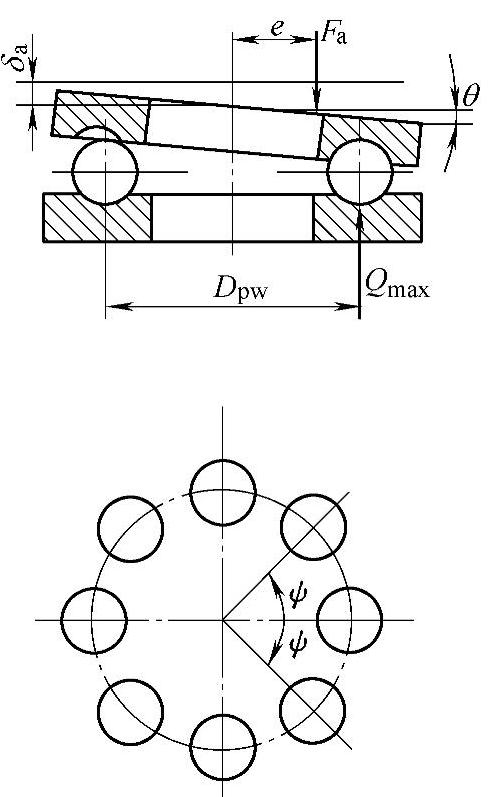
图2 - 29 单向推力轴承的载荷分布

对球轴承：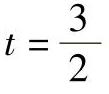

对滚子轴承：t=1.1

由轴承受力平衡可得

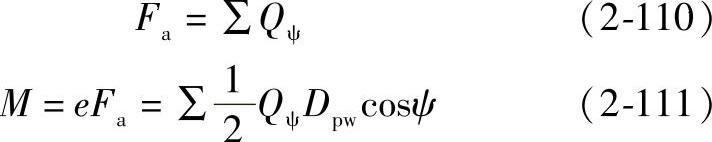
将式（2-109）代入，并引入载荷分布积分J_a、J_M可得

式中

由式（2-112）和式（2-113）可得

在表2-14中列出了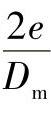与J_M、J_a的对应关系。J_M、J_a的数值同样可在图2-30中查出。

表2-14 单向推力轴承（α=90°）载荷分布积分J_M、Ja

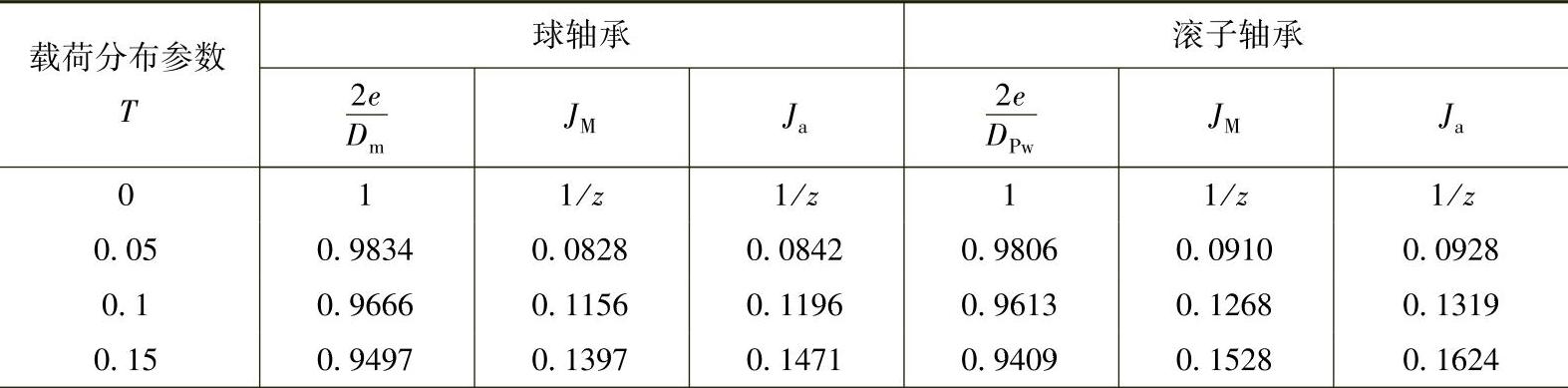
（续）

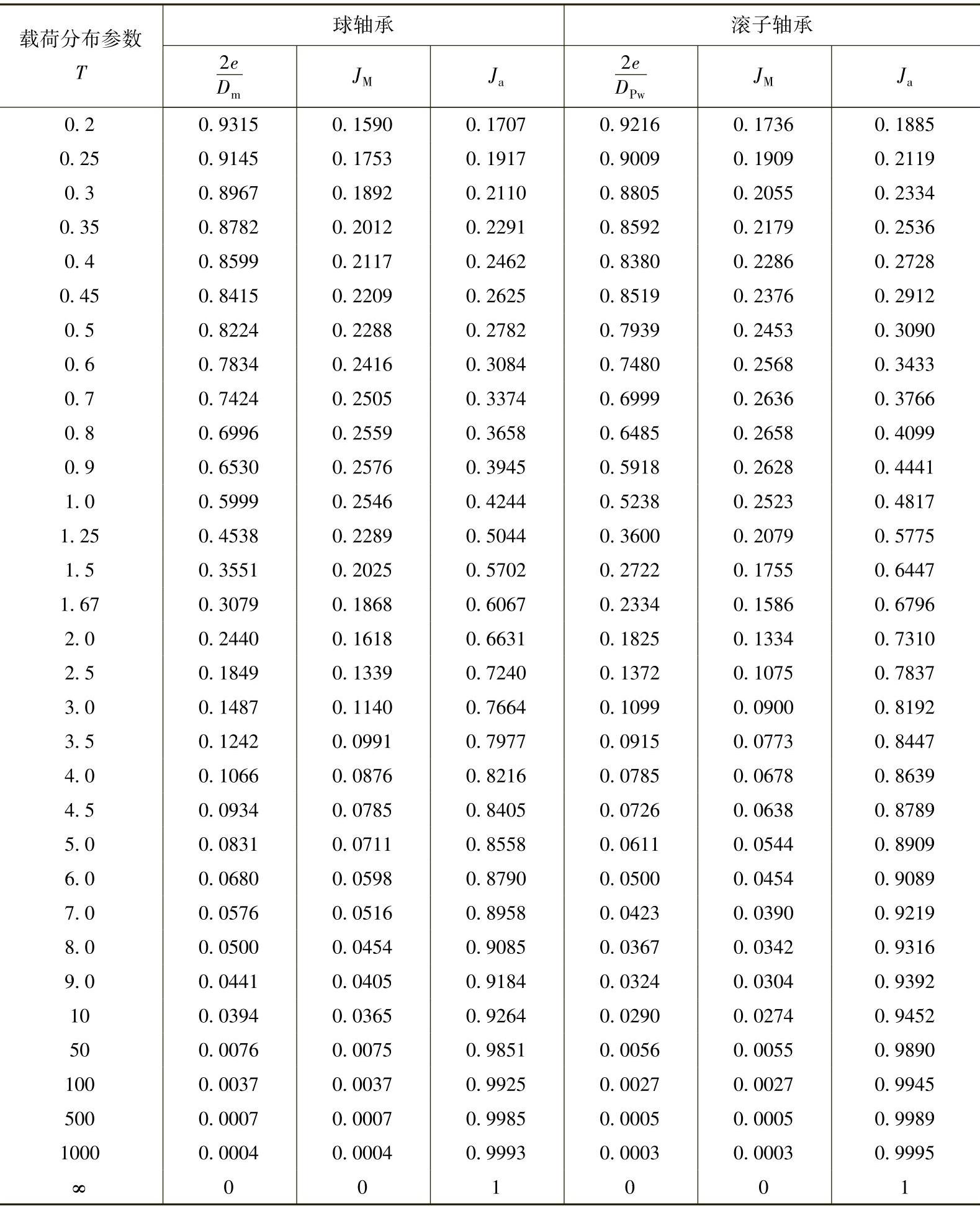
由表2-14所列之值可得（对单向推力轴承）当时

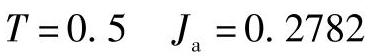
在这种情况下，轴承中仅由半圈滚道承受载荷，由式（2-112）可得

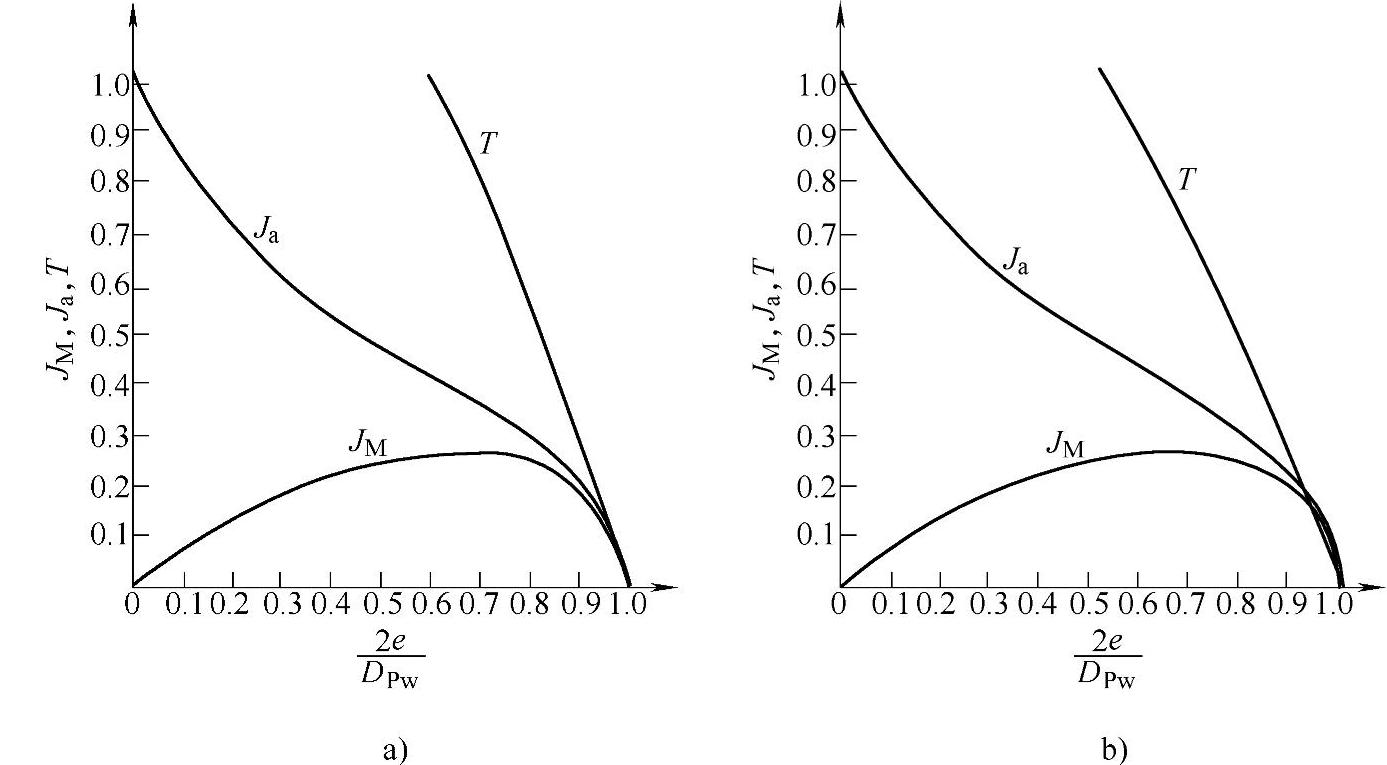
图2 - 30 单向推力轴承的载荷分布积分J_M、Ja

a）球轴承 b）滚子轴承

当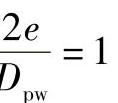时，轴承中仅有一个滚动体承受载荷。如果2e﹥D_pw，则轴承套圈将倾斜分离。因此单向推力球轴承仅能承受的偏心载荷。