单列角接触球轴承 单列角接触球轴承有以下几种结构形式：1）分离型角接触球轴承。图1-18 角接触球轴承a）单列角接触球轴承 b）双列角接触球轴承 c）角接触球轴承结构2）非分离型角接触球轴承。双列角接触球轴承 双列角接触球轴承的特点是可以同时承受径向和轴向载荷的联合载荷，限制轴的两方向的轴向位移。图1-21 两面带防尘盖和两面带密封圈的双列角接触球轴承图1-22 有装球缺口的双列角接触球轴承的安装......
2025-09-29
角接触轴承载荷分布优化分析
【摘要】：角接触球轴承和圆锥滚子轴承可以同时承受径向载荷和轴向载荷，如图2-23所示。但是单个角接触球轴承和圆锥滚子轴承不能单独承受纯径向载荷。图2 - 23 角接触球轴承图2 - 24 角接触轴承内圈载荷分布图此类轴承中的载荷分布与载荷角β有关。轴承中任一滚动体承受的载荷，由滚动体与滚道接触处的变形量来决定。表2-12 单列角接触轴承的载荷分布积分Jr、Ja 单列圆锥滚子轴承32315承受的径向载荷Fr=40kN，轴向载荷Fa=15kN，试计算轴承中最大滚动体载荷Qmax。
角接触球轴承和圆锥滚子轴承可以同时承受径向载荷和轴向载荷，如图2-23所示。但是单个角接触球轴承和圆锥滚子轴承不能单独承受纯径向载荷。
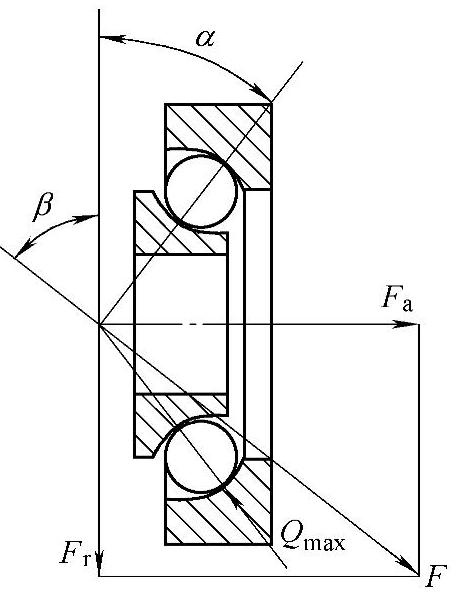
图2 - 23 角接触球轴承
图2 - 24 角接触轴承内圈载荷分布图
此类轴承中的载荷分布与载荷角β有关。如果β小于某一数值，则轴承中仅有一部分套圈滚道承受载荷，如果β超过某一数值，则套圈滚道的整个圆周都承受载荷。
图2-24是角接触球轴承内圈滚道所受载荷的示意图。轴承中任一滚动体承受的载荷，由滚动体与滚道接触处的变形量来决定。
如果在径向载荷Fr和轴向载荷Fa作用下，轴承内圈中心相对于外圈中心平移了δa和δr，则内圈滚道上距最大载荷滚动体为ψ处的A点将移至A1点，如图2-25所示。在此处，滚动体与内、外圈滚道总的弹性变形量为
δψ=δasinα+δrcosαcosψ （2-73）
ψ=0处为承受载荷最大的滚动体与套圈滚道的接触处。在这里，最大的弹性变形量为
δmax=δasinα+δrcosα （2-74）
如引入载荷分布参数T，则
那么式（2-73）可改写为
图2 - 25 角接触轴承套圈相对移动图
载荷分布参数T表示轴承中载荷区范围的大小，如图2-26所示。
图2 - 26 角接触轴承载荷分布与T的关系
T﹤1仅有部分滚道承受载荷；
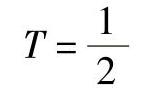δa=0，在这种情况下内、外圈滚道仅有相对径向位移，轴承中仅有半圈滚道承受载荷；
T≥1整个滚道都承受载荷；
T=∞ δr=0，在这种情况下，内、外套圈仅有相对轴向位移，所有滚动体都承受载荷。
如将式（2-58）代入式（2-76）中可得
式中，对球轴承
，对滚子轴承t=1.1。
由轴承受力平衡可得
(https://www.chuimin.cn)
式中 Jr——载荷分布的径向积分；
Ja——载荷分布的轴向积分；
ψ0——为载荷区弧度之半。
在式（2-76）中，如δψ=0，则可得
在T≤1时
cosψ0=1-2T （2-82）
当T﹥1时
ψ0=π
由式（2-78）和式（2-79）可得
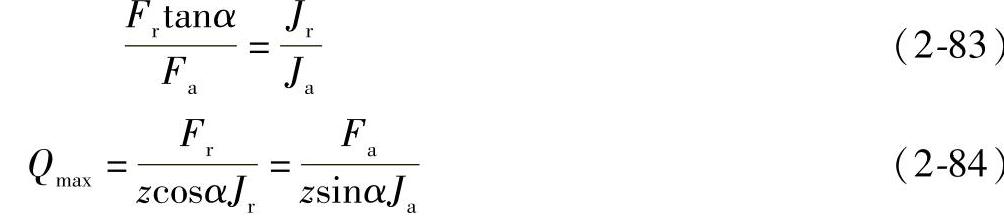
单列角接触轴承的Jr、Ja与载荷分布参数T和
之间的关系，列于图2-27和表2-12中。表列之值适用于承受载荷后接触角α不变化的轴承。对于在承受载荷后接触角变化的轴承，如将实际接触角代入，则表列之值可近似使用。
图2 - 27 角接触轴承的Jr、Ja
a）点接触 b）线接触
对于角接触轴承，为了保持至少有半圈滚道承受载荷，即T=0.5时，所需的轴向载荷为：
对球轴承：Fa=1.22Frtanα
对滚子轴承：Fa=1.26Frtanα
如果轴向载荷低于上述之值，则轴承中载荷区将减小，承受载荷的滚动体数量也减少。如果Fa=Frtanα，则轴承中只有一个滚动体承受载荷。
表2-12 单列角接触轴承的载荷分布积分Jr、Ja
【例8】 单列圆锥滚子轴承32315承受的径向载荷Fr=40kN，轴向载荷Fa=15kN，试计算轴承中最大滚动体载荷Qmax。32315轴承的结构尺寸为：Dw=14.989mm，z=19，α≈10°30′
【解】 首先计算出
由图2-27或表2-12可查得
Jr=0.244
由式（2-84）可得
相关文章
- 详细阅读
-
小流量工况下叶片载荷分布优化详细阅读
由图5.2可知，NPSHa=1.89m时，空泡集中在叶片吸力面进口靠前盖板附近，并且空化区域较小。NPSHa=1.48m［对应图5.1中的B点］时，叶片表面压力分布仍较均匀，叶片进口附近低压区范围缩小，即叶片进口处叶片载荷接近零，出口处压力降低。NPSHa=0.86m［对应图5.1中的C点］时，叶片表面压力分布发生变化，即叶片载荷在S=0～0.2处变小。......
2025-09-29
-
如何选用轴承的接触疲劳寿命？详细阅读
事实上，在安装、润滑、密封正常的情况下，绝大多数滚动轴承的破坏是接触疲劳破坏。因此一般情况下可按接触疲劳寿命选用轴承。如引入转速系数fn、寿命系数fh则可较快地算出轴承的寿命。要求轴承寿命过短，则使用中需经常拆换轴承。......
2025-09-29
-
如何选用适合额定静载荷的轴承？详细阅读
对于低速旋转或缓慢摆动的轴承，应按额定静载荷和接触疲劳寿命两种方法分别计算，选取尺寸较大的轴承。在按额定静载荷选用轴承时，还应注意与轴承相配合部件的刚性。表1-17 允许静载荷系数fs由式求出C0值，查附录和轴承样本，即可确定应选用的轴承代号。如果硬度低于上述范围，则可用上述公式近似确定轴承的额定动载荷和额定静载荷。......
2025-09-29
-
叶片载荷分布在设计流量工况下的设计优化详细阅读
图5.5叶轮中间截面上叶片载荷分布由图5.5可知，NPSHa=2.09m［对应图5.1中的A点］时，叶轮叶片表面压力分布较均匀，在叶片进口吸力面处压力最小，出口处压力最大。NPSHa=1.27m［对应图5.1中的C点］时，叶片表面压力分布发生变化，即叶片载荷在S=0～0.3处明显变小。当NPSHa=1.07m［对应图5.1中的D点］时，叶片表面压力分布变化较显著，即叶片载荷在S=0～0.6处变得较小，尤其是在S=0.4～0.6处接近零，叶片前端60%的部分基本不做功，造成离心泵扬程突降。......
2025-09-29
-
如何计算滚动轴承的载荷传递——滚动体载荷详细阅读
滚动轴承承受的载荷是通过滚动体由一个套圈传向另一个套圈的。即αi=αe由作用于滚动体上载荷的平衡可知，外圈对滚动体作用的载荷Qe与内圈对滚动体的载荷Qi数值相等，方向相反。所以由式（2-1）可得 7307B角接触轴承承受纯轴向载荷Fa=1kN，求作用于每个钢球上的滚动体载荷是多少？图2-4 圆锥滚子轴承的滚动体负荷外圈作用于滚动体上的载荷为内圈作用于滚动体上的载荷分为两部分。......
2025-09-29
-
载荷和驱动分析详细阅读
图2.3三个工作室的相位关系α1、α2、α3分别表示三个工作室相应的偏心轴转角，它们之间的关系为图2.3三个工作室的相位关系α1、α2、α3分别表示三个工作室相应的偏心轴转角，它们之间的关系为pg1、pg2、pg3分别表示三个工作室相应的气体压力，并分别作用于各自的转子工作面上，各自的总作用力均通过转子中心。......
2025-09-29
-
轴承接触角及表示方法简析详细阅读
图2-1所示为几类轴承接触角的表示方法。图2-2 圆锥滚子轴承和非对称球面滚子轴承的接触角a）圆锥滚子轴承 b）非对称球面滚子轴承在图2-2中：α——表示轴承的接触角，因为外圈滚道无挡边，所以也就是滚动体与外圈接触处的接触角；αi——表示滚动体与内圈滚道接触处的接触角；αd——表示滚动体与内圈滚道挡边接触处的接触角。向心球轴承和角接触球轴承，在轴向载荷作用下接触角将变大，详见本章第5节。......
2025-09-29
相关推荐