首页理论教育径向游隙对向心轴承载荷分布的影响分析

径向游隙对向心轴承载荷分布的影响分析

2023-06-26 理论教育版权反馈

【摘要】：表2-10 向心轴承JrJr与载荷分布参数T的关系也可由图2-22中查出。再由径向游隙Gr的数值计算出载荷分布范围角，最后计算出作用于每个滚动体上的载荷数值。Gr=0 Qmax=1.43kNGr=0.025mm Qmax=1.647kNGr=0.050mm Qmax=1.833kN而球轴承寿命与最大滚动体载荷的三次方成反比，因此，轴承中径向游隙的大小对轴承寿命的影响是很大的。

很明显，如果轴承中有径向游隙G_r，则轴承中承载区将减小，最大滚动体载荷将增加。如果在径向载荷F_r作用下，轴承内圈相对于外圈在径向平移了δ_r，如用G_r表示轴承的径向游隙，则

因此

引入

式中，T为向心轴承的载荷分布参数，如T=0.5则G_r=0；如T﹤0.5则G_r﹥0，说明轴承中有径向游隙；如T﹥0.5，则说明轴承中有负游隙，即G_r﹤0，轴承处于预紧状态。

将式（2-70）代入式（2-69）中，可得

由式（2-58）可推得

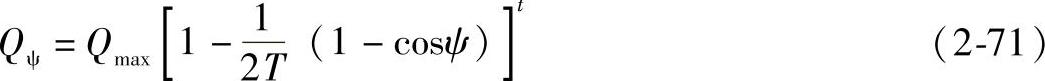
对球轴承：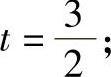

对滚子轴承：t=1.1。

由上式可得出承载范围的大小为

cosψ₀=1-2T （2-72）

如果计算出的则说明轴承中仅有一个滚动体承受载荷。

由轴承受力平衡可得

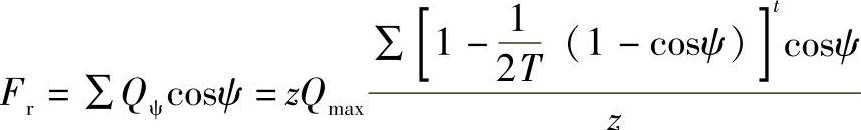
引入载荷分布积分Jr

则可得与式（2-65）相同的表达式：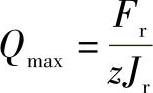

式中J_r的数值列于表2-10中。

表2-10 向心轴承Jr

J_r与载荷分布参数T的关系也可由图2-22中查出。

由式（2-70）可知，载荷分布参数T与径向游隙、最大载荷滚动体和套圈滚道的弹性变形量δ_max有关，因此如果已知径向载荷F_r和径向游隙G_r则可计算出作用于每个滚动体的载荷。步骤如下：首先决定轴承的弹性变形常数K，然后再求出轴承中最大的滚动体变形δ_max。再由径向游隙G_r的数值计算出载荷分布范围角，最后计算出作用于每个滚动体上的载荷数值。下面用例7说明决定滚动体载荷的方法。

【例7】深沟球轴承6208承受的径向载荷F_r=2.94kN，试计算在径向游隙为G_r=0.025mm和G_r=0.050mm时，作用于每个滚动体上的载荷。6208深沟球轴承中钢球直径为：D_w=12.7mm，钢球数为：z=9，沟曲率系数为：f_i=f_e=0.515。

图2 - 22 向心轴承的Jr

【解】 1）由表2-7和式（2-46）可查得弹性变形常数为

2）先假定最大滚动体载荷为

Q_max=1.47kN

由式（2-42）可算出

δ_max=0.000181×1470¹/3mm=0.0235mm

3）当径向游隙为：G_r=0.025mm时，由式（2-70）可得载荷分布参数T的第一次近似值为

4）由表2-10所示，用插入法求得与T相对应的J_r值为

J_r=0.1975

5）由式（2-65）可计算出Q_max的第一次近似值为

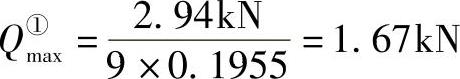
6）根据Q_max的第一次近似值可再假定：

Q_max=1.667kN

则可得出

δ_max=0.0255mm

由δ_max计算出

T=0.3356

由表2-10查出

J_r=0.1977

再由式（2-65）可得Q_max的第二次近值为

Q^②_max=1.653kN

7）根据Q_max的第二次近似值再假定：

Q_max=1.647kN

则可求得

δ_max=0.0253mm

T=0.3348

J_r=0.1975

再由式（2-65）计算出Q_max的第三次近似值为

Q^③_max=1.654kN

因此取Q_max=1.647kN，已足够准确。

8）

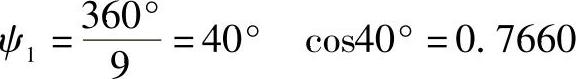
由式（2-71）可得

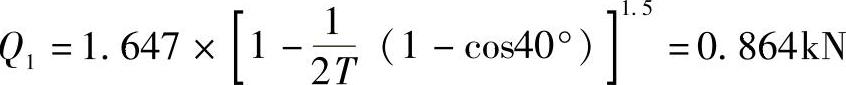
9）由式（2-72）可算出载荷分布范围角为

ψ₀=70°45′

而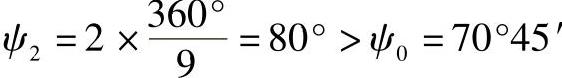

所以 Q₂=Q₃=0

10）与上述相同的步骤可计算出径向游隙G_r=0.50mm时各滚动体上的载荷分布：

Q_max=1.833kN

Q₁=0.750kN

Q₂=Q₃=0

在径向游隙G_r=0.025mm和G_r=0.050mm两种情况时各滚动体载荷的数值列于表2-11中。

表2 - 11 不同径向游隙时的滚动体载荷

对比例6的结果和表2-11中滚动体载荷的数值可知，随着径向游隙的增大，最大滚动体载荷的数值也增大。

G_r=0 Q_max=1.43kN

G_r=0.025mm Q_max=1.647kN

G_r=0.050mm Q_max=1.833kN

而球轴承寿命与最大滚动体载荷的三次方成反比，因此，轴承中径向游隙的大小对轴承寿命的影响是很大的。