轴承钢的热处理工序为淬火→冷处理→回火→稳定化处理等几步。要求轴承的套圈在热处理后变形小，只允许出现轻微的脱碳，因此在大批量生产时，要采用自动化程度较高的热处理操作系统。轴承的热处理主要是淬火＋低温回火处理，获得回火马氏体＋细小的碳化物颗粒＋极少量的残留奥氏体。采用网带炉处理轴承钢的热处理工艺参数见表7-9。表7-12轴承零件淬火处理后常见的质量缺陷和防止措施（续)6)轴承零件的冷处理。......
2023-08-18
点接触轴承弹性变形常数K计算方法
【摘要】：对点接触由式可得各类轴承弹性变形常数K的计算公式列于表2-5中。式可简化为式可简化为对钢制滚动轴承，如果内外圈滚道沟曲率系数相同，则式可简化为其中如果f已知，则由式可求出F（ρ），由表2-2查出与F（ρ）相应的Cδ，即可由式计算出k值。由不同的f计算出的k值列于表2-7和图2-16中。
式（2-29）和式（2-36）计算出的弹性趋近量δ，是滚动体与一个套圈滚道接触处的弹性变形量。滚动体与内、外圈滚道接触处总的弹性变形量为
δn=δi+δe （2-41）
式中 δi——滚动体与内圈滚道接触处的弹性趋近量；
δe——滚动体与外圈滚道接触处的弹性趋近量；
δn——滚动体与两套圈滚道接触处总的弹性变形量。
对点接触由式（2-29）可得
各类轴承弹性变形常数K的计算公式列于表2-5中。对一个给定的轴承来说，因为主曲率已知，所以K是一常数。
在球轴承中，与轴向平面垂直的主平面内的曲率较小，如果忽略该平面内滚道的主曲率，则可使公式简化。式（2-18）可简化为
式（2-20）可简化为
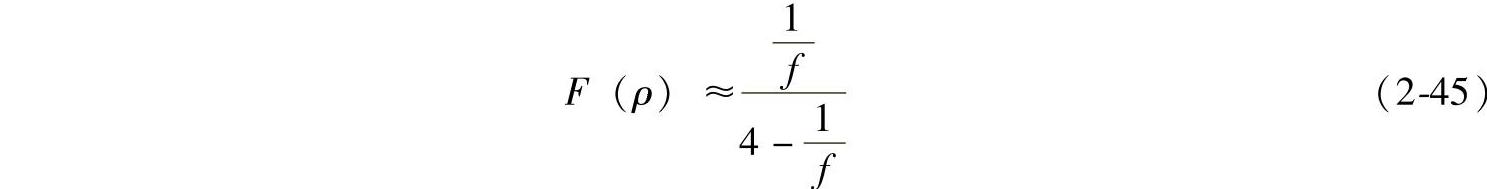
对钢制滚动轴承，如果内外圈滚道沟曲率系数相同，则式（2-43）可简化为
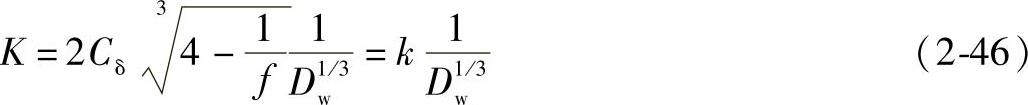
其中
如果f已知，则由式（2-45）可求出F（ρ），由表2-2查出与F（ρ）相应的Cδ，即可由式（2-47）计算出k值。
由不同的f计算出的k值列于表2-7和图2-16中。
表2-7 k值表
表2-7中的数值是Q的单位为N时的数值，图2-16中的纵坐标是Q的单位为kgf时的k值。
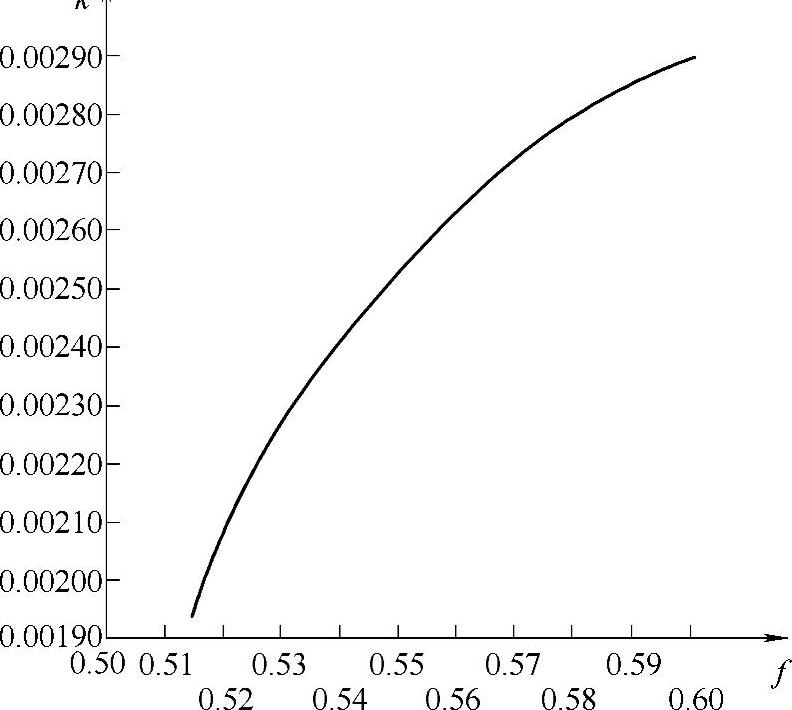
图2 - 16 球轴承的k与f关系图
对线接触，如为钢制的轴承，则由式（2-36）可得
式中：
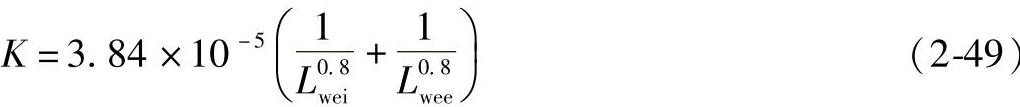
式（2-48）和式（2-49）中，Q的单位是N。
有关滚动轴承应用手册的文章
- 详细阅读
-
常数和位点的结合计算方法详细阅读
图2.2.52-en与不同浓度dsDNA相互作用的常规脉冲伏安图及摩尔结合分数Xb与[DNA]的非线性拟合曲线常规脉冲伏安法经常应用于测定电活性小分子和生物大分子之间的结合常数，因为常规脉冲伏安法的极限电流能准确地反应具有电活性分子的游离态和dsDNA结合态配合物之间的形态转换[26，45]。......
2023-06-22
-
滚动轴承的塑性变形及其优化详细阅读
随着载荷的增大，塑性变形量也逐渐增大。实验证明，即使在很小的载荷作用下，轴承中也产生塑性变形。图2-51 δ与Q2/3的关系图图2-52 塑性变形δs与载荷Q的关系图2.塑性变形的计算公式滚动轴承中塑性变形的计算公式为对点接触：式中 δs——滚动体和一个滚道接触处总的塑性变形量；Q——滚动体载荷；Dw——滚动体直径；ρⅠ1；ρⅡ1；ρⅠ2；ρⅡ2——接触物体Ⅰ、Ⅱ在主平面1、2中的主曲率。......
2023-06-26
-
角接触球轴承的单个使用、DT配置和四点接触球详细阅读
在轴承实际使用中，如果作用于轴承上的载荷小于上述各公式估算出的Frmin或Famin，则为了防止轻载打滑，必须对轴承进行预紧。表2-63 最小轴向载荷系数Ka[1]通过滚动体中心与轴承轴线垂直的平面称为轴承的径向平面。包含轴承中心线的平面称为轴向平面。[3]式中对点接触所以取ε=3而对线接触：，，ε=4但是因为滚子轴承的接触形式很多，既有点接触，又有线接触，为统一滚子轴承的寿命计算方法，取ε=。......
2023-06-26
-
滚动轴承的当量动载荷计算方法详细阅读
由上节所述可知，滚动轴承的额定动载荷是在假定的运转条件下确定的。在此假定载荷的作用下，轴承的寿命和实际载荷条件下的寿命相同，因此把此假定载荷称为当量动载荷，用P表示。式或式是滚动轴承当量动载荷计算的基本公式。图2-43和图2-44的曲线还可以表示为了得到相同的当量动载荷P，径向载荷Fr与轴向载荷Fa之间的关系。因此在确定这些类型轴承的当量动载荷P时，必须考虑接触角的变化。......
2023-06-26
-
双支承轴轴承载荷计算方法详细阅读
多数情况下，可以把双支承轴的结构作为静定问题处理，利用力的平衡方程计算出支承反力，把得出的支承反力作为轴承载荷进行寿命计算。在大多数轴承应用场合下，把双支承轴作为静定问题，已能足够精确地确定轴承所承受的载荷。在这种支承结构中如果轴的刚性较大，仅考虑轴承的变形时，可用下述方法计算轴承载荷。由第2章第3节所述可知，各列承受的载荷大小与轴向载荷Fa和径向载荷Fr的相对数值有关。......
2023-06-26
-
土木工程材料的变形性质及弹性模量详细阅读
常见土木建筑工程材料的弹性模量如表1.2所示。表1.2几种常用土木材料的弹性模量2.塑性变形当外力除去后，材料仍保留一部分残余变形且不产生裂缝的性质称为塑性。图1.4低碳钢的变形曲线3.徐变材料在恒定应力作用下，其应变随时间而缓慢增长，这种现象称为材料的徐变或蠕变。......
2023-09-01
-
建筑力学第3版：组合变形的计算方法及应用详细阅读
当这六种力（或力矩）中只有某一个作用时，杆件就会产生基本变形。图10-1杆件同时有两种或两种以上的基本变形的组合时，称为组合变形。图10-2对发生组合变形的杆件计算应力和变形时，可先将荷载进行简化或分解，使简化或分解后的静力等效荷载，各自只引起一种简单变形，分别计算，再进行叠加，就得到原来的荷载引起的组合变形时应力和变形。当然，必须满足小变形假设及力与位移之间呈线性关系这两个条件才能应用叠加原理。......
2023-08-26
相关推荐