如何选用轴承的接触疲劳寿命？

在滚动轴承中，承受载荷而又相对运动的接触表面（滚道或滚动体表面），由于接触应力反复作用，首先在接触表面下一定深度处形成裂纹，继而发展至接触表面，使表面金属成片状疲劳剥落。事实上，在安装、润滑、密封正常的情况下，绝大多数滚动轴承的破坏是接触疲劳破坏。因此一般情况下可按接触疲劳寿命选用轴承。

1.3.1 滚动轴承疲劳寿命计算方法

按接触疲劳寿命选用轴承的基本公式为

对球轴承：

对滚子轴承：

式中 L——额定寿命（百万转）；

C——额定动载荷（kN）；

P——当量动载荷（kN）。

在实际计算中，以百万转为单位不太方便，一般用工作小时数表示轴承的寿命。这时

式（1-1）和式（1-2）可改写为

对球轴承：

对滚子轴承：

式中 L_h——额定寿命（h）；

n——轴承工作转速（r/min）。

在车辆用轴承中，一般用公里（km）数表示轴承的寿命，这时式（1-1）和式（1-2）可改写为：

对球轴承：

对滚子轴承：

式中 L_k——以公里数表示的寿命（km）；

D——车轮直径（mm）。

如引入转速系数f_n、寿命系数f_h则可较快地算出轴承的寿命。还可利用简化的图表来查出轴承的寿命。下面介绍几种简化计算的图表。

（1）转速系数f_n、寿命系数f_h在式（1-3）、式（1-4）中引入转速系数f_n和寿命系数f_h，有

对球轴承：

对滚子轴承：

对球轴承：

对滚子轴承：

这样式（1-3）、式（1-4）可改写为

在表1-2中列出了球轴承和滚子轴承f_n、f_h和L_h的换算公式。

表1-2 寿命系数和转速系数的换算公式

表1-3列出了n与f_n的对应表。

表1-4列出了L_h与f_h的对应表。

表1-3 转速系数f_n

（续）

（续）

表1-4 寿命系数f_h

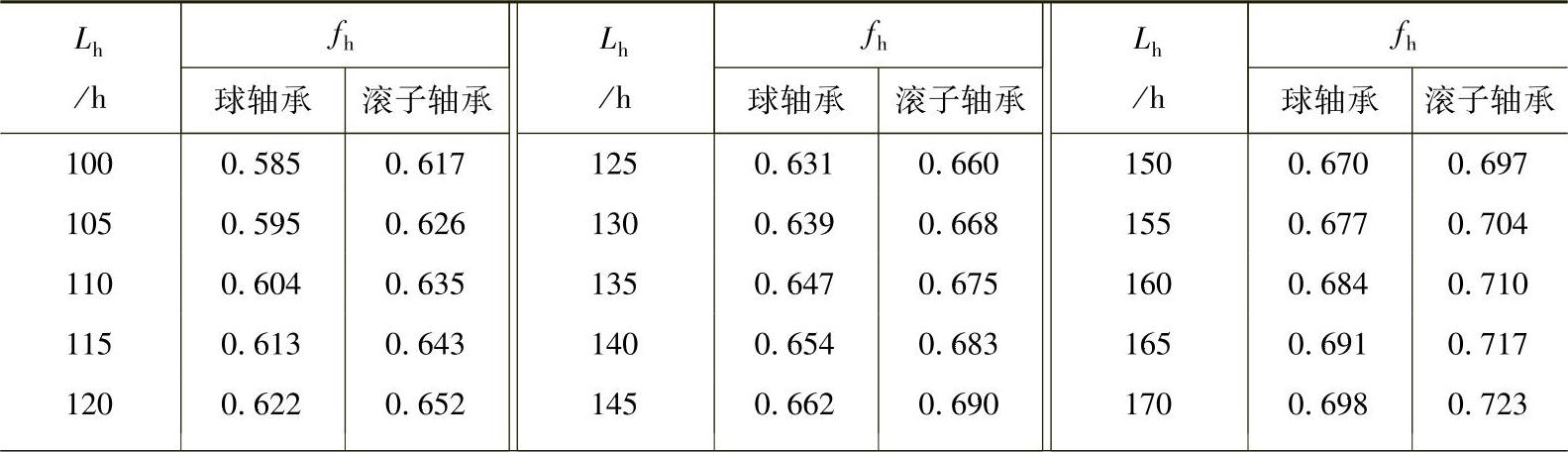
（续）

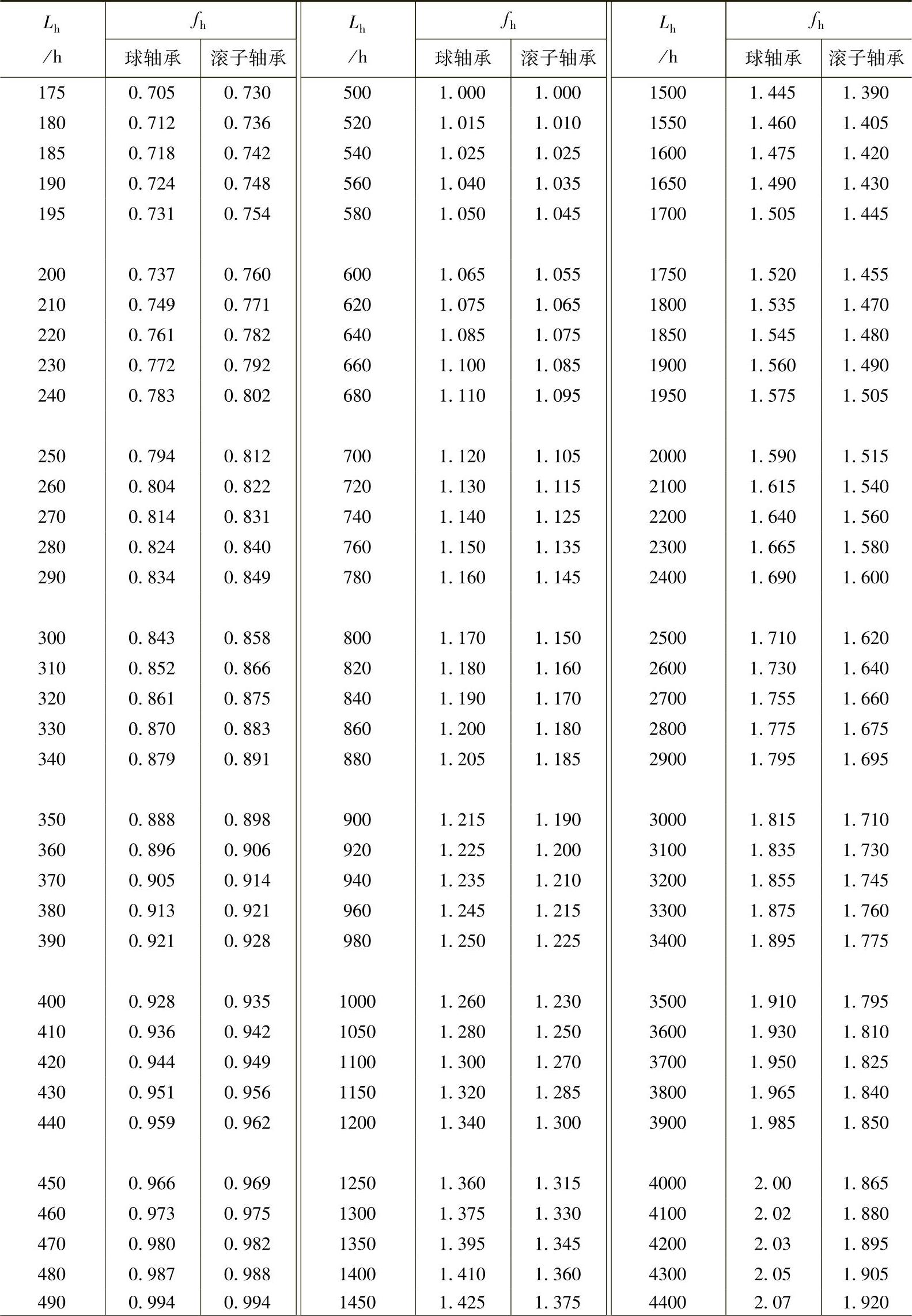
（续）

注：L_h为额定疲劳寿命。

（2）已知轴承寿命L_h和轴承转速，直接查出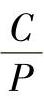值 由式1-11可知，当量动载荷P的值可以由作用于轴承上的载荷算出。只要知道轴承转速n和要求的轴承寿命L_h，则可很快地由表1-5中查出所需球轴承的C值，由表1-6中查出所需的滚子轴承C值，因而可由附录或轴承样本中查出所需的轴承代号。

（3）已知L（百万转）直接查出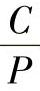值 如果知道了以百万转为单位的轴承寿命L值，则可更快速地从图1-1中或表1-7中查出所需的C值，从而从附录或轴承样本中查出具体的轴承代号。

表1-5 与L_h、n相应的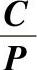（球轴承）

（续）

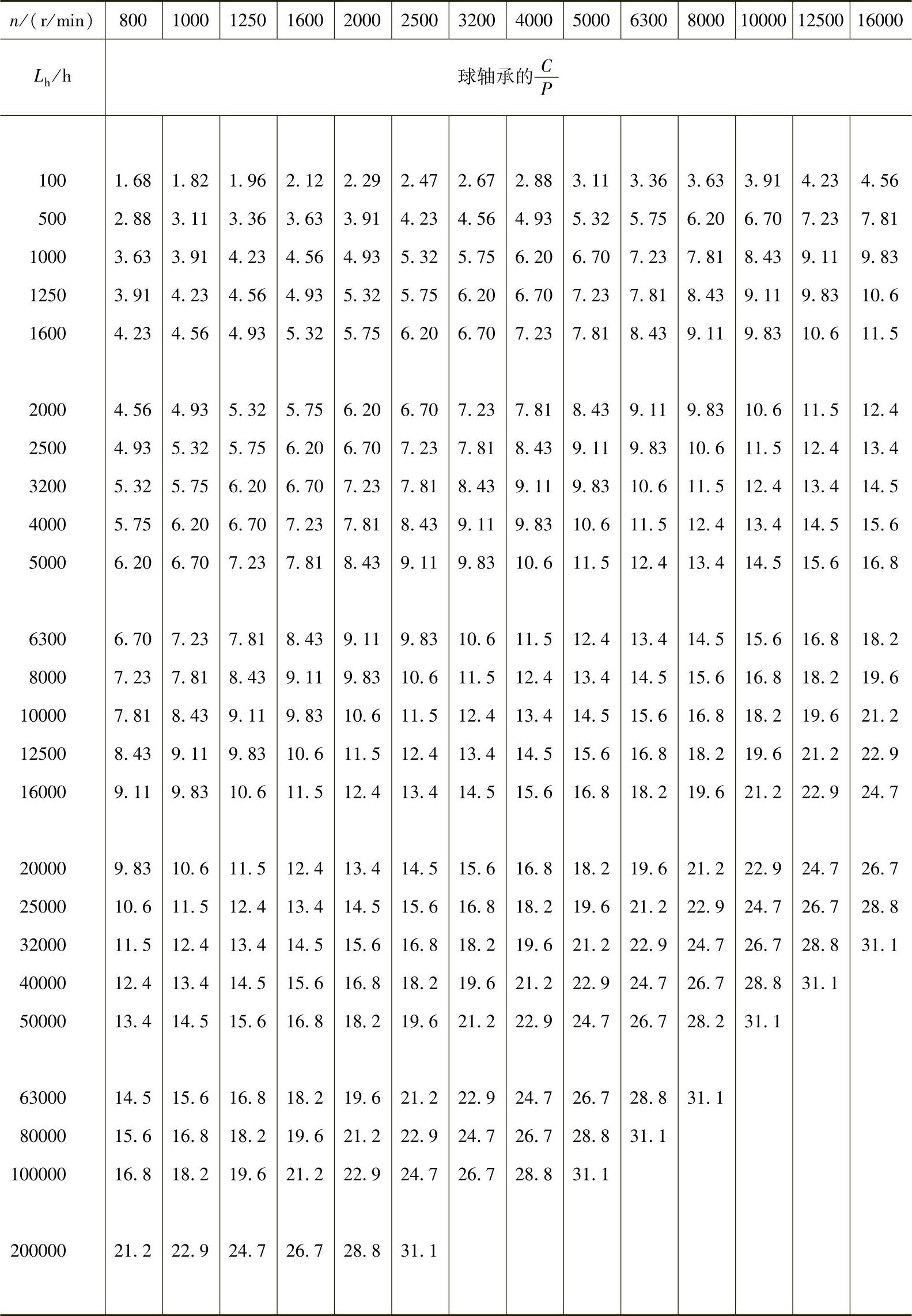
表1-6 与L_h、n相应的（滚子轴承）

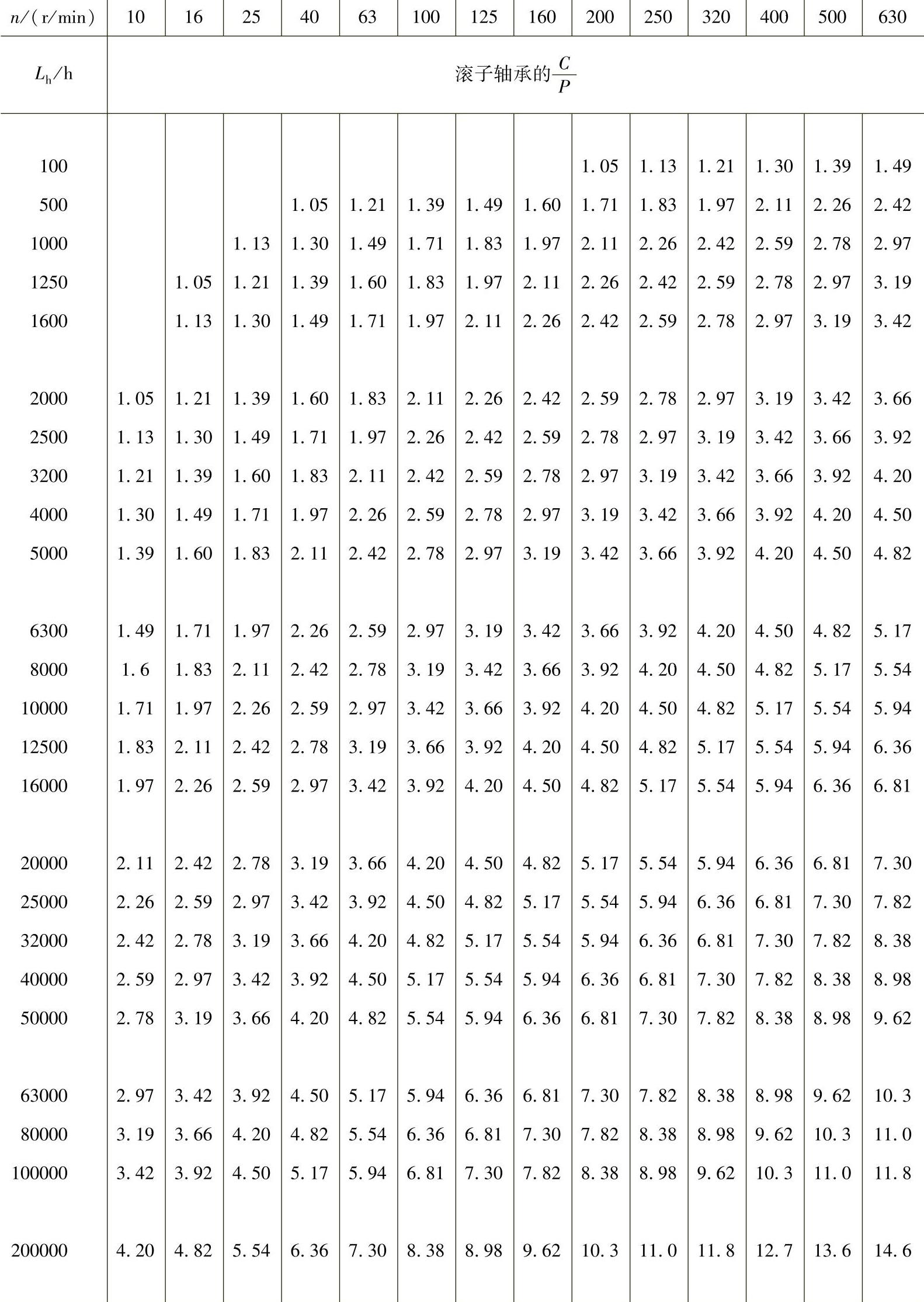
（续）

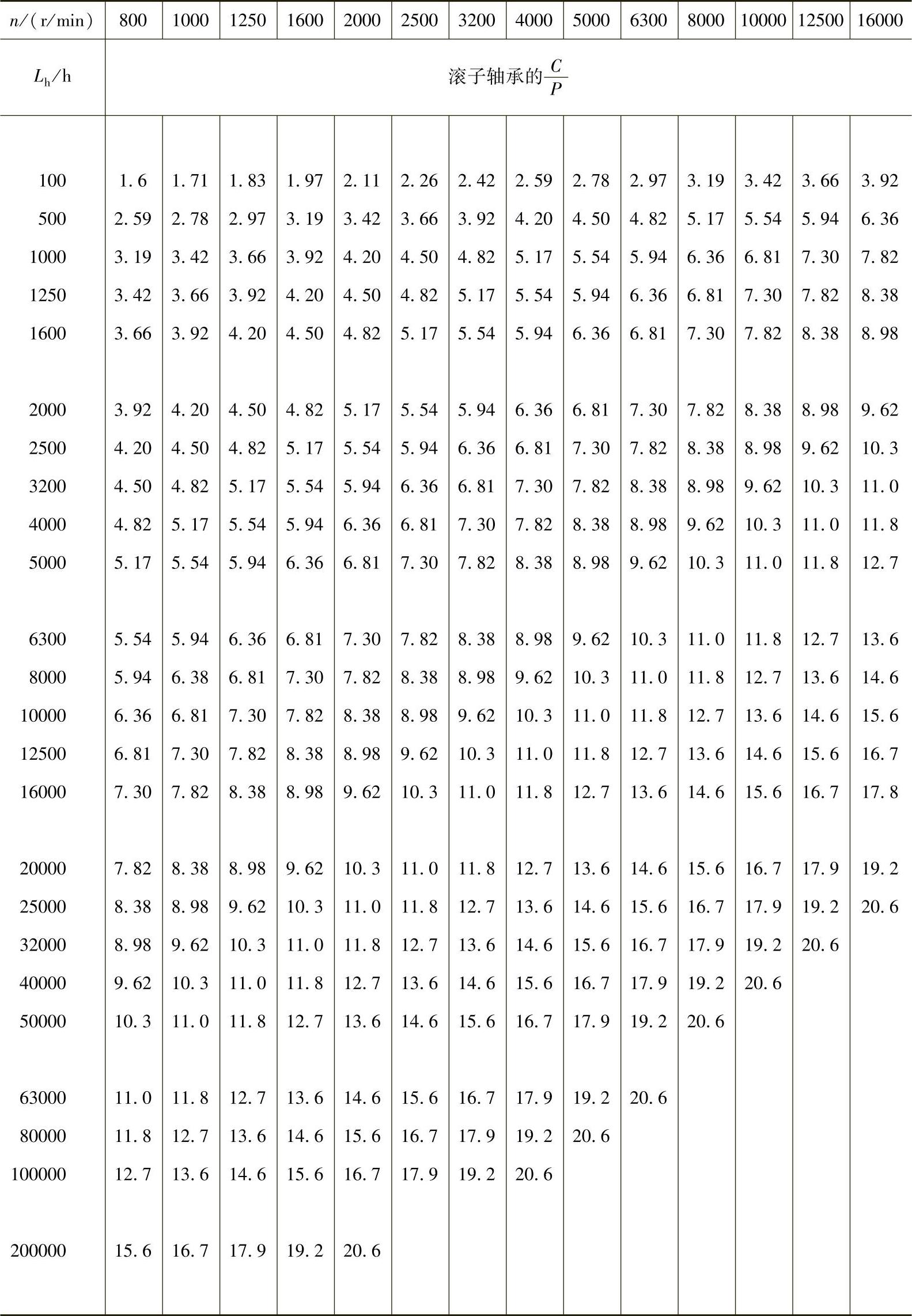
表1-7 L与相应值

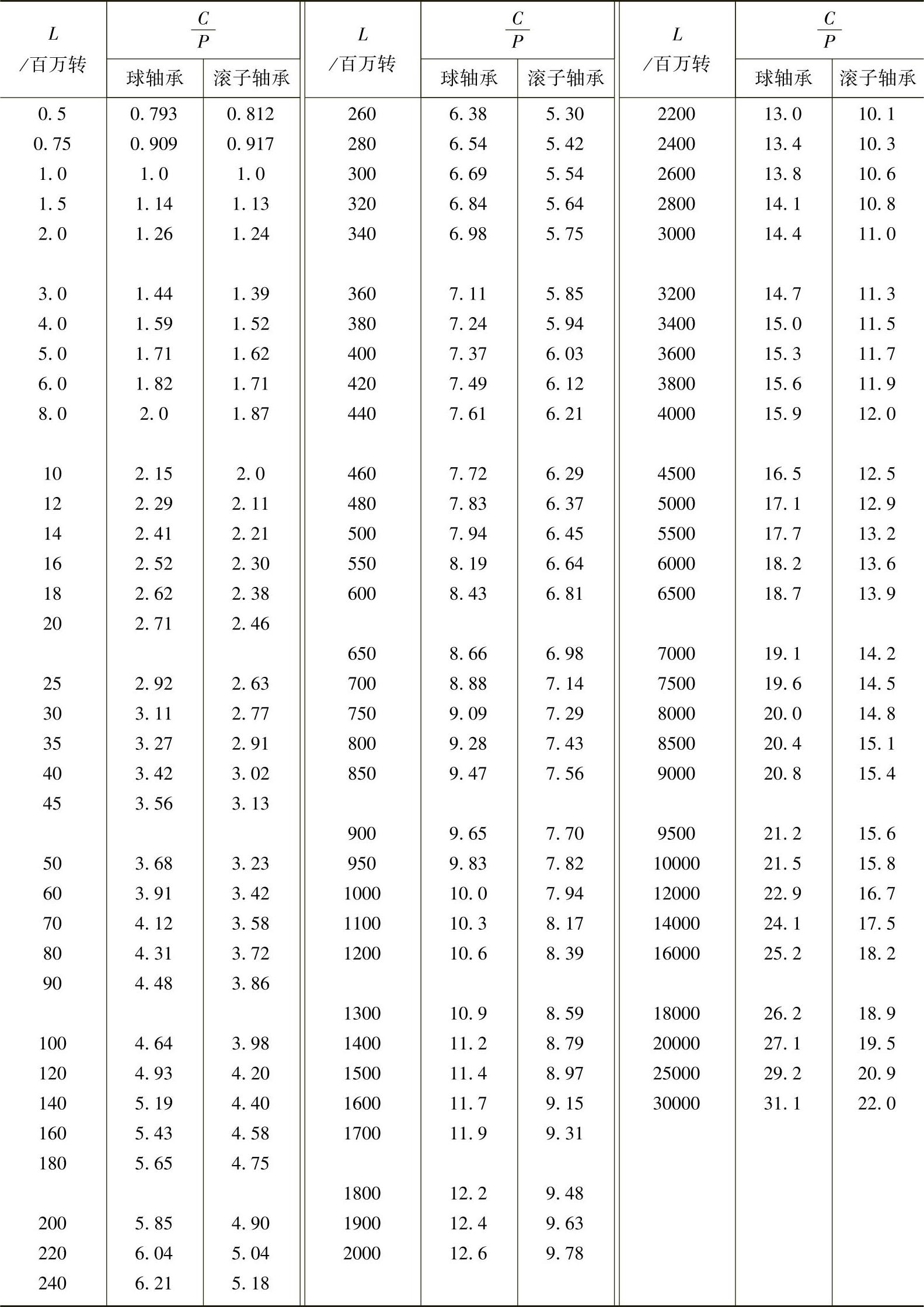
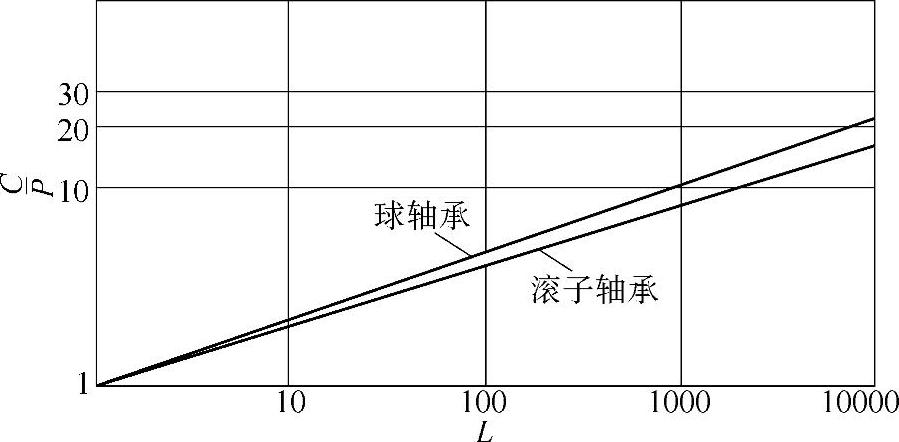
图1-1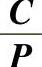与L关系图

1.3.2 滚动轴承的使用寿命

在选择轴承时，应合理地提出对使用寿命的要求。要求轴承寿命过长，则所选轴承结构尺寸大，机械笨重，不经济。要求轴承寿命过短，则使用中需经常拆换轴承。一般是根据机器的大修期确定使用寿命的要求。表1-8列出了各种工作条件下，轴承使用寿命的推荐值。

表1-8 各种机械轴承使用寿命的推荐值

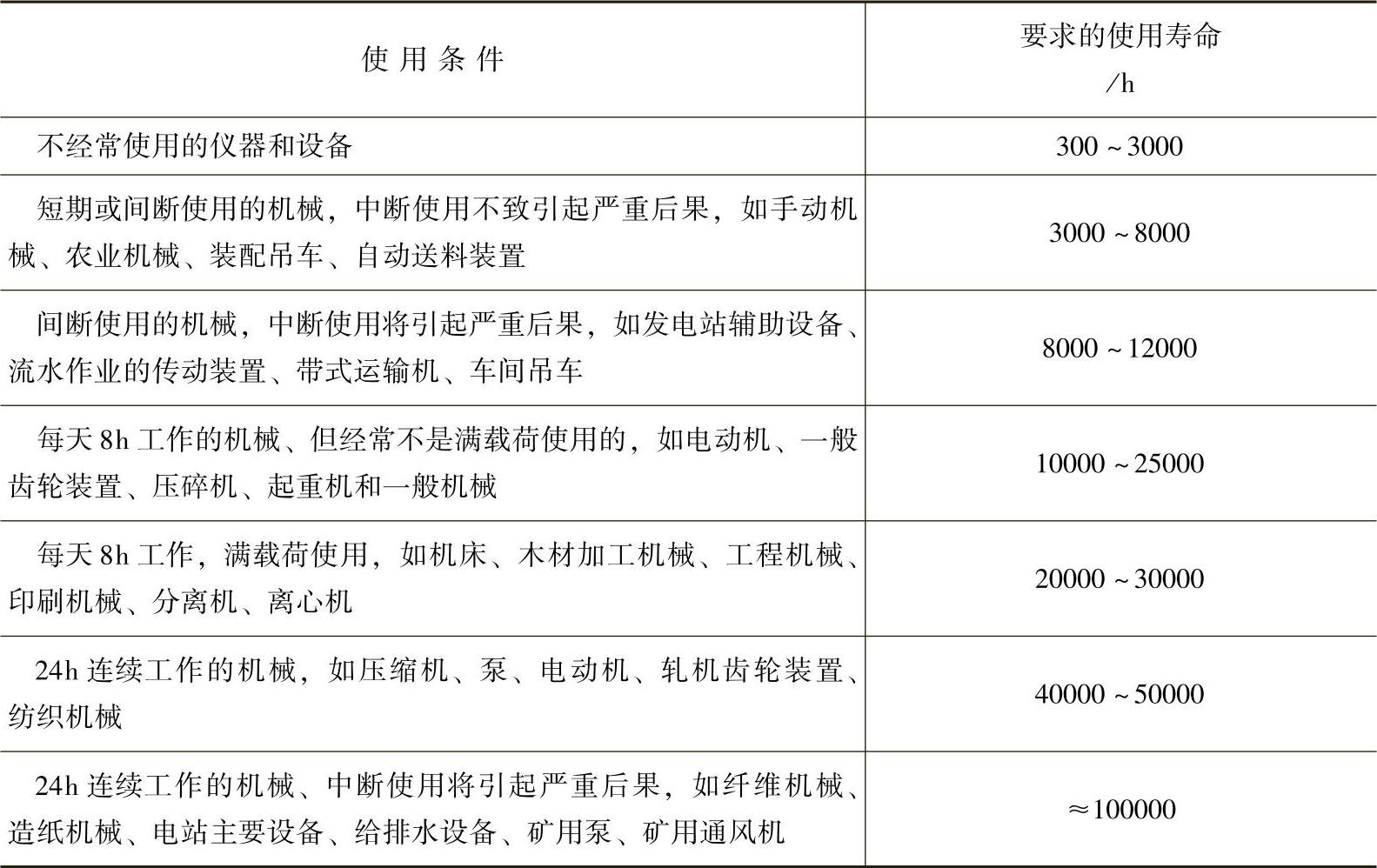
表1-8是SKF公司推荐的各种机械设备中轴承寿命的推荐值。

用寿命系数f_h是FAG公司的习惯用法。表1-9推荐了各种机械选用轴承时推荐的f_h值。表1-10是各种工况下推荐的f_h值。

表1-8、表1-9、表1-10推荐的使用寿命值，均系国外几家大轴承公司，根据多年选用轴承经验提供的。取值时应参考我国同类机械的使用经验确定。

表1-9 f_h参考值

表1-10 与工作状况和对机械影响程度有关的f_h参考值

1.3.3 当量动载荷P的计算方法

同时在径向载荷F_r和轴向载荷F_a作用下时，需将实际作用于轴承上的载荷转换成当量动载荷P，才能进行轴承寿命计算。当量动载荷是一假定载荷，在此载荷的作用下，轴承的寿命与实际载荷作用下的寿命相同。尤其对于向心球轴承和角接触球轴承，在计算当量动载荷时还需考虑在实际轴向载荷F_a的作用下引起的轴承接触角的变化。关于当量动载荷P的详细情况将在第2章第6节予以介绍。

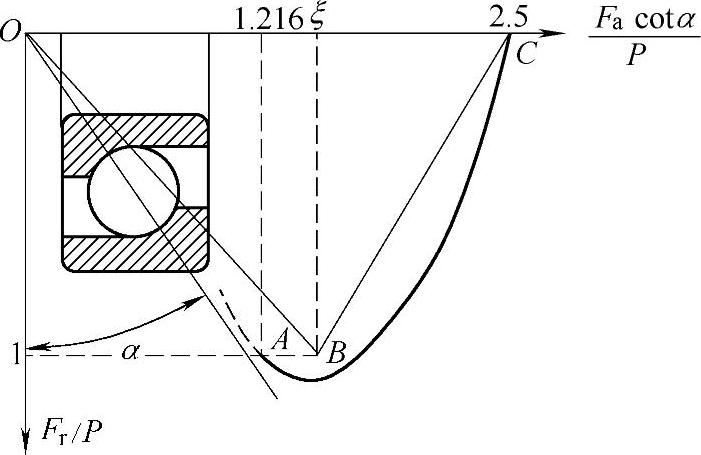
图1 - 2 轴承的等寿命曲线

（1）滚动轴承的等寿命曲线及当量动载荷计算公式根据Lundberg-Palmgren关于滚动轴承寿命的理论，可以作出各类轴承的等寿命曲线，如图1-2所示。图中横坐标用表示，纵坐标用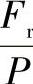表示。凡径向载荷F_r和轴向载荷Fa的不同组合落在曲线AC上时，各点的轴承寿命相同。图1-2所示为角接触球轴承的等寿命曲线。为了简化当量动载荷的计算，用折线AB、BC代替曲线AC。A点的坐标为：

（球轴承）或1.266（滚子轴承）。由此可得出

对球轴承：

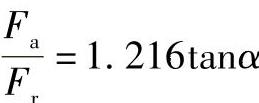
对滚子轴承：

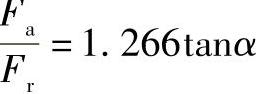
这正好符合滚动轴承中半圈滚道受载时的受载情况（详见第2章第3节）。

B点的坐标为

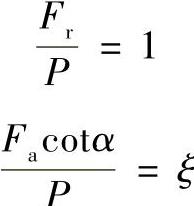
ζ是与轴承结构和类型有关的参数。对深沟球轴承：ζ=1.1；对角接触球轴承：ζ=1.25；对圆锥滚子轴承：ζ=1.5。当F_a与F_r的比值稍大于半圈滚道受载时，对轴承寿命没有影响。当F_a与F_r的比值小于A点的值时，轴承不能正常工作，此段曲线用虚线表示。

由图1-2中可得出当量动载荷P的简化计算公式，用判断参数e表示折线AB和BC相交点的情况：

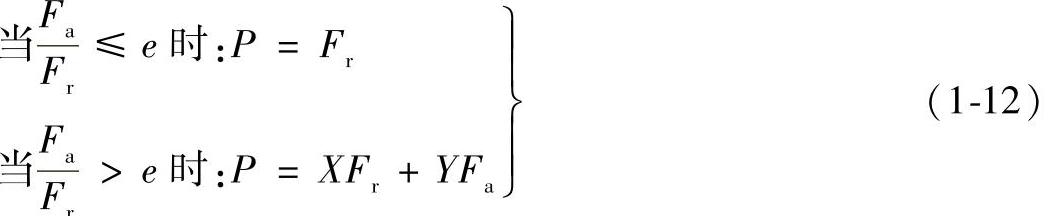
式中 X——径向系数；

Y——轴向系数；

e——判断参数，与ζ和接触角有关；

α——轴承的实际接触角。球轴承的α值随轴向载荷而变化，可借助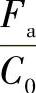的数值来间接反映接触角的大小，详见第2章第6节。

在附录中，对每种型号的轴承给出了具体的径向系数X、轴向系数Y和判断参数e的数值，因而可以进行当量动载荷P的计算。

深沟球轴承和角接触球轴承的当量动载荷的计算，要考虑在轴向载荷作用下接触角的变化，大致可分以下几个步骤：

1）计算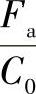值。C₀为额定静载荷。如果轴承代号尚未确定，可暂估一个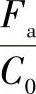的数值，待型号选定后再验算所估之值是否合适。

2）由附录所列的e、X、Y表中选取对应的e值。

3）判断F_a/F_r是大于或小于e值，再查出相应的X、Y值。

4）由式（1-12）计算出当量动载荷P。

滚子轴承由于接触角不随轴向载荷而改变，因而轴承代号选定后即可由附录中查出相应的X、Y、e值。

（2）相对安装两个角接触球轴承或圆锥滚子轴承的轴向载荷计算 角接触球轴承和圆锥滚子轴承在同时承受径向载荷和轴向载荷时，其载荷作用中心不是在轴承几何宽度中心线与轴中心线的交点，而是在各个滚动体载荷向量与轴中心线的汇交点，如图1-3所示。

图1-3中，两个轴承分别用轴承Ⅰ和轴承Ⅱ表示，a_Ⅰ和a_Ⅱ分别表示载荷作用中心距离轴承外圈大端面的距离。

角接触球轴承和圆锥滚子轴承，在承受径向载荷F_r的同时，将产生一内部轴向载荷，驱使内、外套圈相分离。当两个角接触球轴承或圆锥滚子轴承相对安装时，一个轴承的内部轴向载荷将是另一轴承外加轴向载荷的一部分。因此在计算角接触球轴承或圆锥滚子轴承的轴向载荷时，必须考虑这种内部轴向载荷。

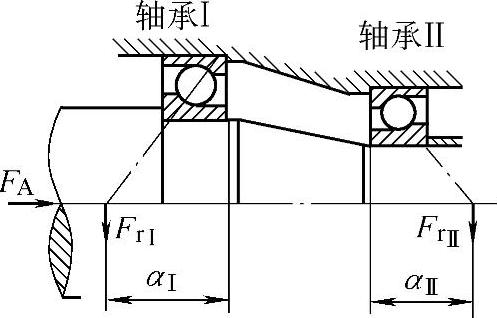
图1 - 3 角接触球轴承的载荷作用中心

根据滚动轴承中载荷分布理论（详见第2章第3节），内部轴向载荷S为

对角接触球轴承：

S=1.216tanα·F_r

对圆锥滚子轴承：S=1.266tanα·F_r

因为角接触球轴承的接触角α是随F_a而变化的，而其判断参数：e=1.25tanα。圆锥滚子轴承的接触角α是不变化的，而其轴向系数为：Y=0.4cotα。而e值和Y的数值均可由附录或轴承样本中查到。因此为简化计算，内部轴向载荷S的计算公式为

表1-11列出不同安装情况下，轴承Ⅰ和轴承Ⅱ轴向载荷的计算公式。表中上部分是角接触球轴承的示意图，下部分是圆锥滚子轴承的示意图。

由第2章第3节滚动轴承中载荷分布理论可知，角接触球轴承和圆锥滚子轴承在承受径向载荷时要产生内部轴向力趋使轴承套圈相互分离，内部轴向力S为

式中 S——轴承中的内部轴向力；

J_a（T）——载荷分布的轴向积分，可由表2-12查出；

J_r（T）——载荷分布的径向积分，可由表2-12查出；

T——载荷分布参数；

F_r——作用于轴承上的径向载荷。

表1 - 11 相对安装的角接触球轴承或圆锥滚子轴承轴向载荷的计算公式

注：表中：S_Ⅰ，S_Ⅱ——为轴承Ⅰ、Ⅱ的内部轴向力；F_aⅠ，F_aⅡ——为轴承Ⅰ、Ⅱ承受的轴向载荷；F_rⅠ，F_rⅡ——为轴承Ⅰ、Ⅱ承受的径向载荷；F_A——外加轴向载荷。

由S的计算公式中可看出：载荷分布参数T不同时，可得到不同的内部轴向力数值。在外加轴向载荷F_a的作用下，都可由内部轴向力与之平衡。为了保证角接触球轴承和圆锥滚子轴承的正常工作，轴承中至少应有一半滚动体承受载荷，即半圈滚道承受载荷，这时：T=0.5。

由表2-12可查得

对球轴承：

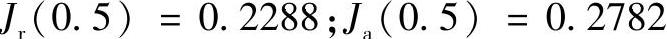
对圆锥滚子轴承：

因而可得，在T=0.5时：

对角接触球轴承：S=1.216tanα·F_r

对圆锥滚子轴承：S=1.266tanα·F_r

表1 - 12 载荷性质系数的近似值

滚动轴承中接触情况比较复杂。对球轴承来说都是点接触，对滚子轴承来说有的是线接触，有的是点接触。为了简化计算，统一取为：

S=1.25tanα·F_r

式中，α是指轴承的实际接触角。对圆锥滚子轴承来说α是指滚动体与外圈滚道接触处的接触角。这些内部结构参数在一般轴承参考资料中无法查到，而由附录A和轴承样本中可查出轴向系数Y和判断参数e的数值。因此可用下式计算出内部轴向力：

对圆锥滚子轴承：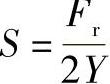

对角接触球轴承：S=eF_r

（3）变动工况下的当量动载荷计算 许多机械在工作中承受变动的载荷，有的转速和载荷都是变动的。由式（1-1）和（1-2）可知，球轴承的疲劳寿命与当量动载荷的3次方成反比，滚子轴承的疲劳寿命与当量动载荷的10/3次方成反比。因此对于重载荷来说，尽管作用的时间很短，但对轴承寿命却有较大的影响。所以在变动工况下必须用平均当量动载荷P_m来计算轴承寿命。

假定轴承在P₁作用下运转了N₁百万转后，将消耗轴承承载能力的，根据疲劳累积损伤原理，则在计算P₂、P₃相继作用了N₂、N₃百万转后疲劳破坏时可得

式中，L₁、L₂、L₃分别为在P₁、P₂、P₃…作用下轴承应达到的寿命。

对球轴承，由式（1-1）可得

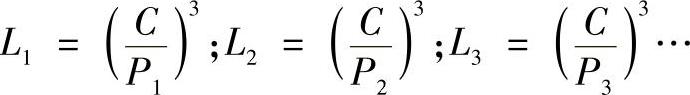
用L表示轴承的总寿命，P_m表示平均当量动载荷，则可得

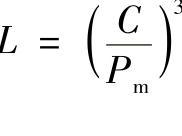
将上述L₁、L₂、L₃、……代入，则可得

对球轴承，平均当量动载荷P_m为

同理可得对滚子轴承有

图1-4所示的变工况情况，可按式（1-15）或（1-16）来计算平均当量动载荷。一般情况对滚子轴承来说，取指数为3误差很小，所以有的资料也推荐对球轴承和滚子轴承统一取指数为3来计算平均当量动载荷。

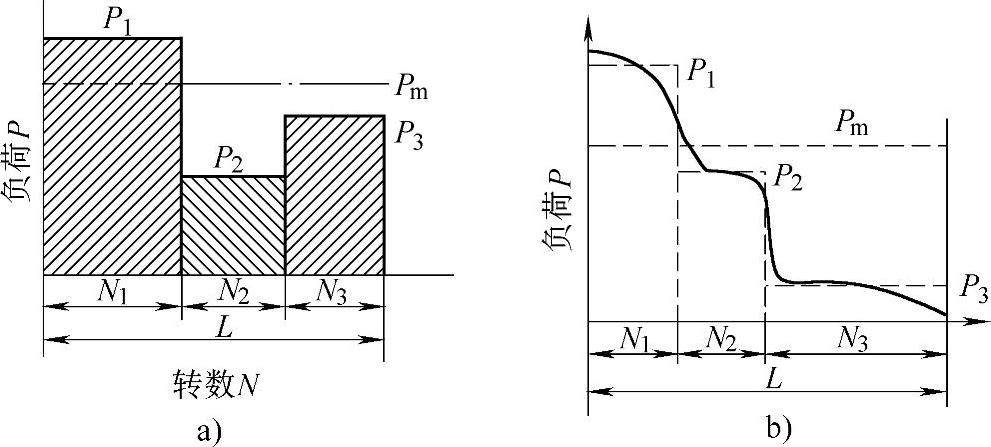
图1 - 4 变工况载荷图

如果当量动载荷随时间而周期变化，则式（1-15）、式（1-16）可写为

对球轴承

对滚子轴承：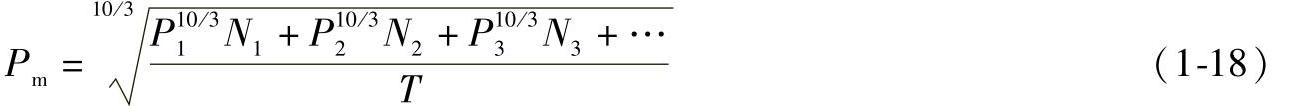

如果轴承依次在P₁、P₂、P₃…作用下运转，其相应转速为n₁、n₂、n₃、…，在每种工况下运转的时间与总的运转时间之比为a₁、a₂、a₃、…，则其平均当量动载荷为

对球轴承：

对滚子轴承：

式中：n_m=n₁a₁+n₂a₂+n₃a₃+…

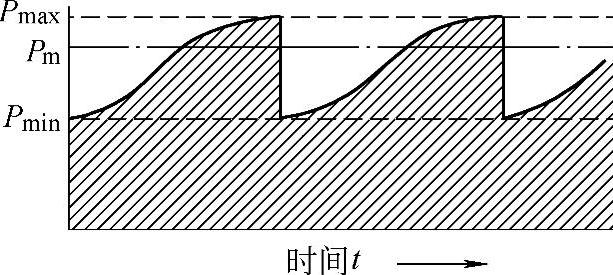
图1 - 5 载荷随时间变化图

如果轴承转速保持不变，而当量动载荷在P_min和P_max之间线性变化或近似线性变化，如图1-5所示，则平均当量动载荷为

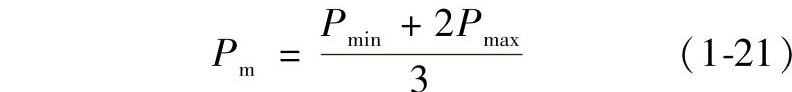
如果轴承载荷由方向和数值都不变化的载荷F₁（如转子重量）和数值不变的旋转载荷F₂（如不平衡量引起的离心力）组成，如图1-6a所示，则其平均载荷可由下式求出：

φ_m之值可由图1-6b中查出。

如果当量动载荷是随时间而变化的函数，其平均当量动载荷P_m可由积分方法求出。

图1 - 6 载荷图

对球轴承：

对滚子轴承：

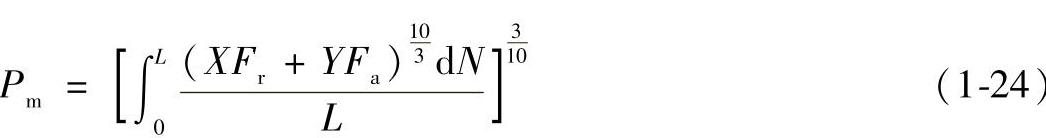
对于载荷变化复杂，而可以作出载荷图的情况，可以用图解法确定其当量动载荷。图解法求平均当量动载荷的步骤如下：

1）以适当比例作出当量动载荷图；

2）将载荷图分为足够小的区间，计算每一区间的末端的P³，然后以适当比例画出P³图；

3）计算出P³图所包围的面积，然后用该图的横坐标除之则可得P³的平均值；

4）计算平均当量动载荷：

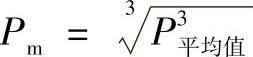
（4）载荷性质对当量动载荷的影响 作用于轴承上的载荷可分为：由轴承支承的物体重量；齿轮皮带等的传动力；回转体不平衡时引起的不平衡载荷和由于机器振动、冲击引起的附加载荷。一般，物体重量和齿轮、皮带的传动力是可以计算出来的，而由振动、冲击引起的附加载荷是很难精确计算出来的。通常是根据机械的工作情况乘以经验系数来计算的。这时当量动载荷为：

P=f_p（XF_r+YF_a） （1-25）

式中 f_p——载荷性质系数，可由表1-12中查出。

1.3.4 寿命修正系数a₁

式（1-1）、式（1-2）是可靠度为90%的计算寿命，即用此公式计算出的寿命，对一批相同的轴承来说，有90%以上的轴承可以达到或超过此寿命。换句话说，就是在达到此寿命之前可能有10%的轴承已破坏。对于一个轴承来说，达到此寿命的概率是90%。这样计算出的寿命为L₁₀。

Tallian分析了2250套轴承的寿命试验结果证实：Lundberg-Palmgren轴承寿命理论，在使用概率在93%和40%之间是与试验数据相符合的。但是随着科学技术的发展，对轴承可靠度的要求较高的应用场合愈来愈多。Tallian提出了可靠度要求高于90%时的可靠度寿命修正系数a₁值。

这时，寿命计算公式为

L_na=a₁L₁₀ （1-26）

式中L_na——任意可靠度要求时的轴承寿命，其中n表示可靠度要求。如可靠度99%时则为L_1a，可靠度为95%时，用L_5a表示；

a₁——可靠度寿命修正系数。

Tallian给出的a₁值如表1-13所示。此可靠度a₁的数值已纳入国际标准ISO281：1990和国标GB/T6391—2003中。

表1-13 可靠度寿命修正系数a₁

因此对高可靠度要求的轴承寿命计算公式为

对球轴承：

对滚子轴承：

1.3.5 影响滚动轴承疲劳寿命的其他因素

（1）温度 本章所介绍的滚动轴承疲劳寿命计算方法，是以额定动载荷C为基础的。而C是在轴承工作温度低于120℃的情况下确定的轴承承载能力，这里的温度是指在轴承外圈处测量的温度。因此如果轴承工作温度超过120℃，则在滚动体和滚道接触处的温度将超过轴承零件的回火温度，轴承零件将丧失原有的尺寸稳定性。所以一般轴承只能在工作温度低于120℃的条件下使用。

对于工作温度高于120℃的轴承，则需向轴承制造厂提出特殊要求，选用经特殊热处理的轴承。在高温条件下工作的轴承，轴承零件的硬度降低，因而使轴承的额定动载荷降低，即

C_T=f_TC （1-29）

式中 f_T——温度系数，列于表1-14中；

C_T——工作温度为T℃时轴承的额定动载荷；

C——由附录A或轴承样本中查出的额定动载荷

表1-14 温度系数fT

（2）游隙 额定动载荷C是在工作径向游隙G_r=0的条件下确定的。如果轴承的工作径向游隙G_r﹥0或G_r﹤0（负游隙，处于径向预紧状态），则将对轴承的承载能力有所影响。

滚动轴承的疲劳寿命与最大滚动体载荷Q_max有很大关系。如果Q_max显著增加，则疲劳寿命将显著降低，因此影响Q_max的一切因素，都将对轴承疲劳寿命产生影响。轴承径向游隙是影响Q_max的一个重要因素。

如用L′表示工作径向游隙为G_r时的轴承寿命，则由第2章所述的额定动载荷理论（见第2章第6节）可推得对球轴承：

对滚子轴承：

式中 L——由式（1-1）和式（1-2）计算出的寿命；

J_r（0.5），J_r（T）——载荷分布积分，可由第2章表2-12查出；

J₁（0.5），J₁（T）——可由第2章表2-17中查出。

根据计算结果，一般载荷分布参数T≈0.7～0.8轴承寿命最长，这时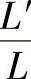约在1.1左右，即轴承工作径向游隙比Gr=0略小时轴承寿命最长。在载荷分布参数T﹤0.5和T﹥0.8的范围内，轴承寿命下降很快。尤其是在负游隙时，轴承发热量大，使轴承寿命下降更快。

（3）硬度

轴承零件的硬度一般为58～64HRC。轴承的额定动载荷C是在此硬度范围内确定的。如果轴承零件的实际硬度低于上述范围，则额定动载荷应降低，降低的数值应通过大量实验来确定。

轴承零件硬度低于HRC58时，据相关资料介绍，轴承额定动载荷降低为

注：由于滚动轴承弹性流体动力润滑研究工作的进展，高质量轴承材料的研究工作取得的成果及环境污染的改善，ISO281：1990引入了寿命修正系数a_xyz，国标GB/T 6391—2003也采用了此系数，详见第2章第7节。

式中 C′——实际硬度下的额定动载荷；

C——由附录或轴承样本中查出的额定动载荷；

HRC——实际洛氏硬度值。

1.3.6 滚动轴承寿命计算举例

【例1 - 1】 某机构中决定选用深沟球轴承作支承，已知轴颈直径d=35mm，承受径向载荷F_r=1.0kN，轴向载荷F_a=0.85kN，轴承转速n=1800r/min，工作中有轻微振动，可取载荷性质系数f_p=1.1。轴承工作温度低于120℃，要求额定寿命L_h﹥5000h。决定轴承代号。

【解】 根据附录所列的几种深沟球轴承的C_0r值，可暂取：

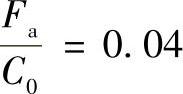
由表中可查出与相对应的值为

e=0.24 X=0.56 Y=1.8

而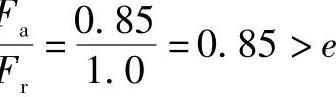

由式（1-25）可算出当量动载荷为

P=f_p（XF_r+YF_a）=1.1×（0.56×1.0+1.8×0.85）kN

=2.299kN

由表1-3查出n=1800r/min时有

f_n=0.265

由表1-4查出L_h=5000h时有

f_h=2.15

由式（1-11）可算出所需额定动载荷为

由附录中查出与之相近的为：6207深沟球轴承，其额定动载荷C_r、额定静载荷C_0r和极限转速n_j分别为

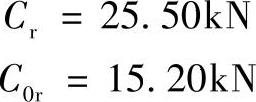
脂润滑时：n_j=8500r/min

油润滑时：n_j=11000r/min

外形尺寸为

d=35mm D=72mm B=17mm

所以选取6207深沟球轴承可以满足所列条件。

【验算】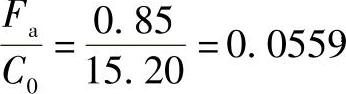

由附录A深沟球轴承中用插入法可求得

X=0.56 Y=1.694

因而可算出当量动载荷P为

P=1.1×（0.56×1.0+0.85×1.694）kN=2.199kN

由表1-2可算出寿命系数f_h值为

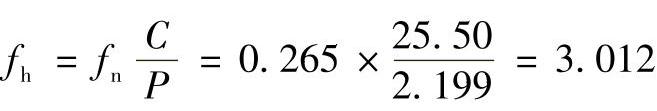
由表1-4可查出

L_h=14000h﹥5000h

由附录可查出

当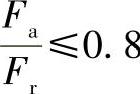时，当量静载荷P₀为

当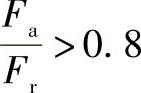

P_0r=F_r时，当量静载荷P₀为

P_0r=0.6F_r+0.5F_a

=0.6×1kN+0.5×0.85kN=1.025kN

因此P_0r﹤C_0r=15.20kN

而极限转速n_j=11000r/min﹥n=1800r/min所以选用深沟球轴承6207可以满足要求。

【例1 - 2】 一传动轴用两个圆锥滚子轴承支承，如图1-7所示，有

F_rⅠ=17kN

F_rⅡ=18kN

F_A=8kN

n=155r/min工作中有中等冲击，可选载荷性质系数f_p=1.5。工作温度低于120℃。

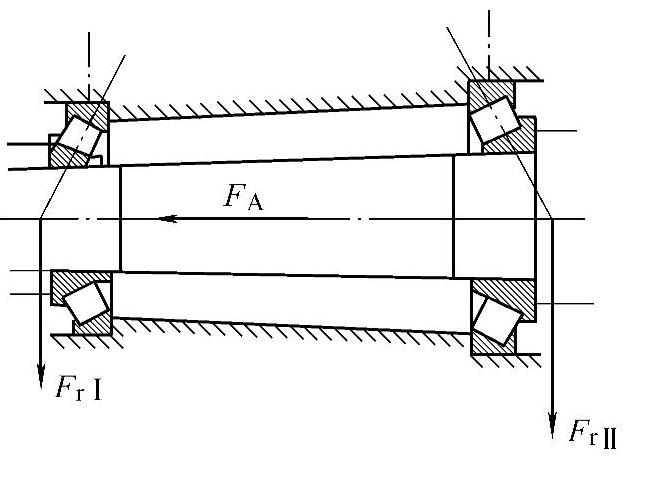
图1 - 7 支承受力简图

决定选用：轴承Ⅰ选用32018

轴承Ⅱ选用32022

【解】 由附录圆锥滚子轴承表中查出轴承Ⅰ、Ⅱ的各项参数列于表1-15中。

表1 - 15 参数表

由式（1-13），内部轴向载荷S为

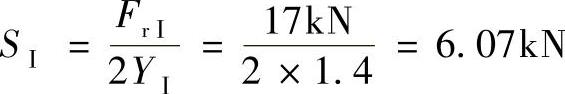
因而S_Ⅰ﹤S_Ⅱ

F_A﹥S_Ⅱ-S_Ⅰ

内部轴向载荷与外加在轴上的轴向载荷F_A符合表1-11中序号5的情况。

所以F_aⅠ=S_Ⅰ=6.07kN

F_aⅡ=S_Ⅰ+F_A=（6.07+8）kN=14.07kN

对轴承Ⅰ：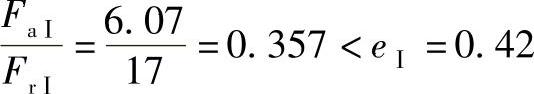

对轴承Ⅱ：

由附录圆锥滚子轴承部分可查得

当F_a/F_r≤e时：P_r=F_r

当F_a/F_r﹥e时：P_r=0.4F_r+YF_a

因此可以算出，当量动载荷为

P_Ⅰ=17kN×1.5=25.5kN

P_Ⅱ=1.5×0.4F_rⅡ+1.4F_aⅡ

=1.5×（0.4×18kN+1.4×14.07）kN=40.35kN

由表1-3中可得当转速n=155r/min时

f_n=0.631

由表1-2中可计算出

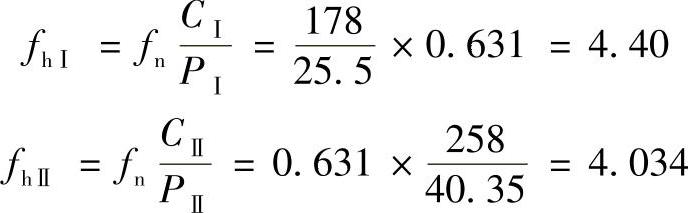
由表1-4中可查得

L_hⅠ=70000h

L_hⅡ=55000h

【例1 - 3】 在高可靠度要求的场合，一传动轴选用短圆柱滚子轴承N2320，在下表所列工况下运转，工作温度低于120℃。计算可靠度为99%时的寿命。

【解】 表1-16为轴承N2320的工作条件。

由公式（1-20）可得平均转速和平均当量动载荷为

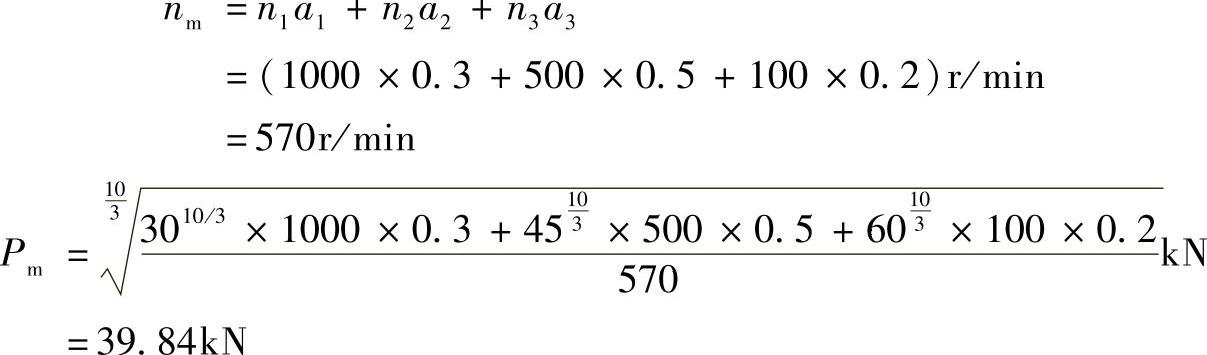
表1-16 轴承N2320的工作条件

由附录圆柱滚子部分查出N2320的额定动载荷为：C=435kN

由表1-13查出，可靠度为99%时的可靠度系数a₁=0.21

由表1-3查出与转速n_m=570r/min相应的转速系数为：f_n=0.427

由式（1-11）和表1-2中可计算出

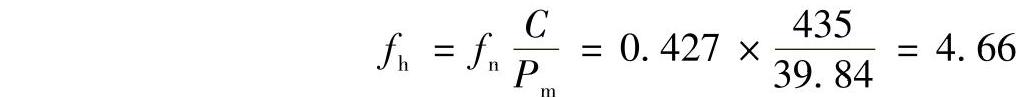
由表1-4可查得

L_h=85000h

再由式（1-26）可计算出可靠度为99%时的轴承寿命为

L_na=a₁L₁₀=0.21×85000=17850h