单变量配方是指只有一个助剂的加入量影响制品的性能的配方。此设计方法一般常用消去法来确定。这个起点一般为原来的生产配方,也可以是一个估计的配方。均分分批试验法是把每批试验配方均匀地同时安排在试验范围内,将其试验结果比较,留下好结果性的范围。该法由于试验结果、试验误差等原因,不易鉴别,所以一般工厂常用均分分批试验法,但当原材料添加量变化较小,而制品的物理性能却有显著变化时,用该法较好。......
2023-06-26
多因素变量配方是指一个配方中有两个或两个以上助剂的加入量影响制品性能的配方。随机确定其加入量,工作量十分繁重,采用科学设计方法,可以准确、快速地得到一个合理的配方。目前常用的多因素变量设计法主要有正交设计法和中心复合试验法,本书重点介绍正交设计法。
(一)正交设计法
正交设计法是一种应用数理统计原理进行科学地安排与分析多因素变量的一种试验方法。
正交设计法最大的优点在于可大幅度减少试验次数,尤其当试验中变量(因素)越多时,减少程度越明显,它可以在众多试验次数中,优选出具有代表性的试验,通过尽可能少的试验,找出最佳配方或工艺条件。有时最佳配方可能并不在优选的试验中,但可以通过试验结果处理,推算出最佳配方。
常规的试验方法为单因素轮换法,即先改变其中一个变量(因素),把其他变量(因素)固定,以求得此变量的最佳值;然后改变另一个变量(因素),固定其他变量(因素),如此逐步轮换,从而找出最佳配方或工艺条件。用这种方法对一个三个变量(因素)的配方,每个变量(因素)三个试验数值(水平)的试验次数为3×3×3=27;而用正交设计法,只需6次即可。
正交设计的核心是一个正交设计表,简称正交表。一个典型的正交表可由下式表达:
LM(bK)
式中 L——正交表的符号;
K——试验中变量的数目,习惯上称其为因素或因子,本书中统称为因素,K值的确定随不同试验而变;
b——每个因素所取的几个试验值数目,一般称为水平或位级,本书中统称为水平,水平值由经验确定,也可在确定前先做一些探索性小型试验,一般要求各水平值之间要有合理的差距;
M——试验次数,一般由经验确定。但作者总结大致规律如下(仅供参考):
对于二水平试验 M=K+1,对于三水平以上试验M=b(K-1);此规律并不全部适用,有时也有例外,如正交表L27(313),具体可参照标准正交表。
指标——正交表的最后一项为试验目的,即指标,它为衡量试验结果好坏的参数,如产品合格率、硬度、耐热温度、冲击强度、氧指数及体积电阻率等。
下面举一实例说明一个正交表的组成。如改善PVC加工流动性的一个试验,加工流动性好坏可用表观黏度表示。表观黏度即为指标,影响加工流动性的参数有三个,即温度(t)、剪切速率(.γ)和增塑剂加入量(RPH),此三个参数即为因素,每个因素取三个不同试验值,即为三水平,如T取150℃、160℃、170℃, .γ取5× 102s-1、1×103s-1、5×103s-1,RPH取20份、30份、40份。
常用的典型正交表如下:
二水平:L4(23)、L8(27)、L12(211)等;
三水平:L6(33)、L9(34)、L18(37)等;
四水平:L16(45)等。
具体正交表排布参见表1-2至表1-6。
表1-2 二水平L4(23)正交表
表1-3 二水平L8(27)正交表
表1-4 二水平L12(211)正交表
表1-5 三水平L9(34)正交表
表1-6 四水平L16(45)正交表
前面提过,一个最佳的配方可能在所做的实验中,也可能不在其中,这就需要对实验结果进行分析处理而找出最佳配方。
实验结果分析可以解决如下三方面的问题:
①对指标的影响,哪个因素主要,那个因素次要,分清主次关系;
②各个因素以哪个水平为最好;
③各个因素用什么样的水平组合起来,指标值最好。
目前常用的分析方法有两种,即直观分析法和方差分析法。
(1)直观分析法
计算每个水平实验取得指标的平均值,进行比较,找出每个因素的最佳水平;几个因素的最佳水平组合起来,即为最佳配方或工艺条件;另外,计算每个因素不同水平所取得不同指标值差,何种因素不同水平之间指标差大,即为对指标最有影响的因素。
具体方法参见下面4.中实例[例一]及实例[例二]。
直观分析法直观、简便,但不能区分因素与水平的作用差异。
(2)方差分析法
这是一种精确的计算方法,结果精确,但手段繁杂。其方法为通过偏差的平方和及自由度等一系列计算,将因素和水平的变化引起实验结果间的差异与误差的波动区分开来,这样来分析正交实验的结果,对下一步实验或投入生产的可靠性很大。
[例一]热固性塑料压制成型配方及工艺条件的确定
(1)设计正交表
指标——硬度合格率。
因素——模板温度、交联时间及交联剂用量三因素K=3。
水平——每个因素取二水平b=2,见表1-7。
表1-7 因素和水平表
实验次数——M=K+1=3+1=4次。
正交表——选L4(23),具体排布如表1-2所示。
(2)按正交表做试验
将结果填入L4(23)正交表中,如表1-8所示。
表1-8 三因素二水平L4(23)正交表
(3)试验结果分析
采用直观分析法。
①计算每一个因素不同水平二次试验的平均值,如下:
将上述计算结果列于表1-8中。表中Ⅰj代表正交表中第j列一水平指标之和;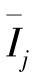 代表Ij的平均值;Ⅱj代表正交表中第j列二水平指标之和;
代表Ij的平均值;Ⅱj代表正交表中第j列二水平指标之和;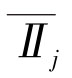 代表的Ⅱj平均值。由于因素A排在第一列,所以
代表的Ⅱj平均值。由于因素A排在第一列,所以 ,同理
,同理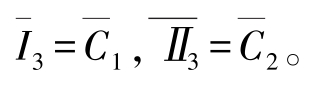
比较 与
与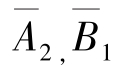 与
与 与
与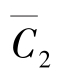 ,可以找出优化条件为
,可以找出优化条件为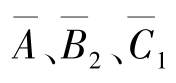 。这次试验不在我们设计正交试验中,而是通过综合比较推算出来的。
。这次试验不在我们设计正交试验中,而是通过综合比较推算出来的。
②还有一个比较三个因素哪一个对指标影响大的问题,可以通过计算极差(Rj)找出,极差值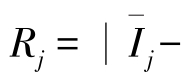
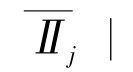 (绝对值),如
(绝对值),如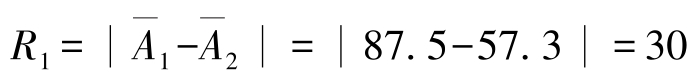 ,将计算结果列于表中,可以看出R1最大,说明模板温度对硬度合格率影响最大。
,将计算结果列于表中,可以看出R1最大,说明模板温度对硬度合格率影响最大。
[例二]PVC复合板配方正交设计
本配方的组分为:聚氯乙烯(PVC)、邻苯二甲酸二辛酯(DOP)、三碱式硫酸铅、石蜡、硬脂酸、氯化聚乙烯(CPE)及赤泥等。
(1)设计正交表
指标——冲击强度、弯曲强度、布氏硬度。
因素——PVC、DOP、硬脂酸不变,分别为100、5、0.4,将三碱式硫酸铅(即三盐、石蜡、CPE、赤泥定为四个因素,即K=4。
水平——每个因素定三个水平,即b=3,见表1-9所示。
表1-9 每个因素确定的三个水平值
注:实验次数M=3×(4-1)=9。
正交表——选L9(34)型正交表,排布参见表1-10。
(2)排布正交表
将试验结果列于表1-10所示的L9(34)型正交表中。
表1-10 L9(34)型正交表
(3)试验结果分析
采用直观分析法。以冲击强度指标为重点,比较其三水平的最佳值可知,A1、B3、C1、D3为最优化组合,此次正交试验A1B3C1D3存在于正交表列第7次试验中,也可直接从表1-10中直接观察到。
对于极差的大小,计算方法为选取极差大的两个水平相减。 R3=34.73-11.55=23.18为各列中最大的,这说明CPE用量是PVC冲击强度的主要因素。
(二)中心复合试验设计法
中心复合试验法是因在中心点做许多重复试验而得名。它是配方变量因素与因素之间关系的一种数学方程,因而又称为回归分析法。
例如,某一塑料制品性能的响应方程式(回归方程式)建立起自变量(即配方组分),再和因变量(塑料制品的物理性能)建立数学表达式。此数学方程式不但包括质的相互关系,还包括量的相互关系。
中心复合试验法可以解决如下几个方面问题。
①首先确定几个特定的配方因子变量之间是否存在相关性。如果没有相关性,就只好单独处理每个因子问题;如果存在相关性,则可找出合适的数学表达式。
②再根据用户提出的几种塑料制品性能指标值,预测出配方因子变量的值;或是相反预测,根据配方因子变量的值,预测出制品性能指标的范围。这两种都可以进行某种控制达到一定的精确度。
③另外还要找出这些因子之间的相互关系,找出哪些因子是重要的,哪些因子是次要的,哪些因子是可以忽略的。通过方程式求出所需性能的配方因子最佳组合,画出某种性能的等高线等。
一般说来,可用一个完全的二次多元式表示制品性能与添加剂用量的关系,然后再求出数个回归系数,进行线性变换,按设计表安排试验,在中心点做重复试验,再进行限制性统计检验。若有问题可改变数学模型进一步研究。
有关塑料配方设计的文章

单变量配方是指只有一个助剂的加入量影响制品的性能的配方。此设计方法一般常用消去法来确定。这个起点一般为原来的生产配方,也可以是一个估计的配方。均分分批试验法是把每批试验配方均匀地同时安排在试验范围内,将其试验结果比较,留下好结果性的范围。该法由于试验结果、试验误差等原因,不易鉴别,所以一般工厂常用均分分批试验法,但当原材料添加量变化较小,而制品的物理性能却有显著变化时,用该法较好。......
2023-06-26

PVC分子内含有的取代氯基,容易导致PVC脱HCl反应,从而引起PVC的降解反应。因此,纯PVC是无法用热塑性方法加工成型的,必须进行加工改性配方设计,使其分解温度高于熔融温度,保证PVC树脂在加工中可熔融流动而不分解。PVC的加工配方设计:一为降低熔融温度,办法为加入增塑剂;二为提高分解温度,办法为加入热稳定剂。此外,对于PVC硬制品,还需加入加工助剂以改善熔体流变特性;对软硬各类制品,还需加入润滑剂以改善流动性和表面性能。......
2023-06-26

其主要目的是未经交联的热固性树脂强度十分低,制成制品后应用范围受到限制。所以说,热固性树脂的加工过程实质为树脂发生交联反应,提高制品强度的过程。为使热固性树脂在加工中交联反应得以发生,往往需要在纯热固性树脂中加入交联剂及固化促进剂等。......
2023-06-26

塑料的黏度改性分为两种情况,绝大多数情况需要降低树脂的黏度,以增加流动性,如大尺寸薄壁注塑产品。尤其是在热固性树脂和PPS树脂的加工配方设计中,加入交联剂是必需的,否则其黏度不能适合于塑化加工。目前,剪切增黏材料主要用于人体防穿刺材料、石油增黏剂和阻尼材料等。(二)降低塑料黏度改性增塑剂是PVC最有效的黏度改性剂,在PVC中加入增塑剂以降低加工温度,提高整体流动性。......
2023-06-26

摩阻性塑料复合材料摩擦因数的大小,显示其制动和传动能力的强弱。摩擦因数的正常恢复性是指摩阻性塑料复合材料的摩擦因数在高温、高速、吸湿等情况下发生衰退后,在正常情况下迅速恢复到正常值的性能。不能恢复或恢复不好会使摩阻性塑料复合材料丧失其使用性能。(二)塑料摩阻改性配方组成黏接性树脂的作用为将增强剂和摩擦性能调解剂黏合在一起,赋予复合制品一定的强度,保证其可加工性能。......
2023-06-26

在既定的配方体系和加工工艺中,所加入助剂能充分发挥其预计功效并达到规定指标。在设计配方时,一定要全面考虑,尽可能不影响其他性能。又如在含有大量吸油性填料的填充配方中,油性助剂的加入量要增大,以弥补被吸收部分。如大部分配方要求助剂与树脂均匀分散,对阻隔性配方则希望助剂在树脂中层状分布。如在PVC稳定配方中,能选铅盐类稳定剂就不要选有机锡类稳定剂;在阻燃配方中,能选硼酸锌则不选三氧化二锑或氧化钼。......
2023-06-26

目前防止塑料水解的方法有:添加水解稳定剂、降低树脂的含水量、添加吸水剂等。多碳化二亚胺常温为黄色至棕色片状粉末,与塑料的相容性好。德国莱茵化学工程塑料部推出新一代Hycasyl水解稳定剂系列产品,主要用于PU树脂;另一个品种为活性抗水解剂Stabaxol P,可用于所有包含酯键或通过聚合作用合成的聚合物,如PET、PBT、PU、TPU、TPEE、PA和EVA等。......
2023-06-26

(一)塑料弹性体增韧机理弹性体增韧的机理很多,目前最成熟的为银纹-剪切带理论。要求加入弹性体的粒度要小,分散要均匀。(二)塑料弹性增韧材料可用于塑料增韧的弹性体很多,按不同方法可分为如下几类。属于此类的弹性体有ACR、MBS、MABS及MACR等。属于此类的弹性体有CPE及EVA等。用于增韧剂的CPE含氯量为30%~45%之间,属于弹性体范围。......
2023-06-26
相关推荐