叶片泵设计简单算法的优化措施

2023-06-26 理论教育版权反馈

【摘要】：它是由SIMPLE算法的提出人之一Patanker完成的。将上述两方面的思想结合起来，就构成了SIMPLER算法。在SIMPLER算法中，经过离散后的连续方程式用于建立一个压力的离散方程，而不像在SIMPLE算法中用来建立压力修正方程。总体而言，SIMPLER的计算效率要高于SIMPLE算法。它也是SIMPLE的改进算法之一，是由Van Doormal和Raithby提出的。

SIMPLE算法自问世以来，在被广泛应用的同时，也以不同方式不断地得到改进和发展，其中最著名的几种算法包括SIMPLER、SIMPLEC和PISO算法。本节介绍这三种算法，并作简要的对比。

1.SIMPLER算法

SIMPLER是英文SIMPLE Revised的缩写，顾名思义是SIMPLE算法的改进版。它是由SIMPLE算法的提出人之一Patanker完成的。

我们知道，在SIMPLE算法中，为了确定动量离散方程的系数，一开始就假定了一个速度分布，同时又独立地假定了一个压力分布，两者之间一般是不协调的，从而影响了迭代计算的收敛速度。实际上，不必在初始时刻单独假定一个压力场，因为与假定的速度场相协调的压力场是可以通过动量方程求出的。另外，在SIMPLE算法中对压力修正值p′采用了欠松弛处理，而松弛因子是比较难确定的，因此，速度场的改进与压力场的改进不能同步进行，最终影响收敛速度。于是，Patanker便提出了这样的想法：p'只用修正速度，压力场的改进则另谋更合适的方法。将上述两方面的思想结合起来，就构成了SIMPLER算法。

在SIMPLER算法中，经过离散后的连续方程式（1.2-46）用于建立一个压力的离散方程，而不像在SIMPLE算法中用来建立压力修正方程。从而可直接得到压力，而不需要修正。但是，速度仍需要通过SIMPLE算法中的修正方程即式（1.2-25）和式（1.2-26）来修正。

将离散后的动量方程式（1.2-41）和式（1.2-47）重新改写后，有

在SIMPLER算法中，定义伪速度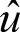与如下：

这样，式（1.2-49）与式（1.2-50）可写为

以上两式中的系数d，仍沿用前面SIMPLE算法所给出的计算公式。同样可写出u_i+1，j与v_i，j+1的表达式。然后，将u_i，j、v_i，j、u_i+1，j与v_i，j+1的表达式代入离散后的连续方程式（1.2-36），有

整理后，得到离散后的压力方程：

式中

需注意到，式（1.2-56）中的系数与压力修正方程式（1.2-37）中的系数是一样的，差别仅在于源项b。这里的源项b是用伪速度来计算的。因此，离散后的动量方程式（1.2-18）和式（1.2-19），可借助上面得到的压力场来直接求解。这样，可求出速度分量u^*和v^*。

在SIMPLER算法中，初始的压力场与速度场是协调的，且由SIMPLER算法算出的压力场不必作欠松弛处理，迭代计算时比较容易得到收敛解。但在SIMPLER的每一层迭代中，要比SIMPLE算法多解一个关于压力的方程组，一个迭代步内的计算量较大。总体而言，SIMPLER的计算效率要高于SIMPLE算法。

2.SIMPLEC算法

SIMPLEC是英文SIMPLE Consistent的缩写，指协调一致的SIMPLE算法。它也是SIMPLE的改进算法之一，是由Van Doormal和Raithby提出的。

由前述可知，在SIMPLE算法中，为求解方便，略去了速度修正方程中的∑a_nbu′_n_b项，从而把速度的修正完全归结为由于压差项的直接作用。这一做法虽然并不影响收敛解的值，但加重了修正值p'的计算量，使得整个速度场迭代收敛效率降低。实际上，当我们在略去∑a_nbu′_nb时，出现一个“不协调一致”的问题。为了能略去a_nbu'_nb而同时又能使方程基本协调，然后在u'_i，j方程式（1.2-25）的等号两端同时减去∑a_nbu′_i_，j有

可以预期，u'_i，j与其邻点的修正值u'_nb具有相同的数量级，因而略去∑a_nb（u′_n_b-u′_i_，j）所产生的影响远比在式（1.2-25）中不计∑a_nbu′_n_b所产生的影响要小得多，于是有

u′_i_，j=d_i，j（p′_i_-1，j-p′_i_，j）（1.2-59）

式中

类似地，有

v′_i_，j=d_i，j（p′_i_，j-1-p′_i_，j）（1.2-61）

式中

将式（1.2-61）和式（1.2-62）代入SIMPLE算法中的式（1.2-30）和式（1.2-31），得到修正后的速度计算式：

式（1.2-63）和式（1.2-64）在形式上与式（1.2-30）和式（1.2-31）一致，只是其中的系数项d的计算公式不同，现在需要按式（1.2-60）和式（1.2-62）进行计算。

这就是SIMPLEC算法。SIMPLEC算法与SIMPLE算法的计算步骤相同，只是速度修正方程中的系数项d的计算公式有所区别。

由于SIMPLEC算法没有像SIMPLE算法那样将∑a_nbu′_n_b项忽略，因此，得到的压力修正值p'一般是比较合适的，因此，在SIMPLEC算法中可不再对p'进行欠松弛处理。但据数值试验，适当选取一个稍小于1的a_p对p'进行欠松弛处理，在一定情况下对加快迭代过程中解的收敛是有益的。

3.PISO算法

PISO是Pressure Implicit with Splitting of Operators的首字母缩写，意为压力的隐式算子分裂算法。PISO算法是Issa于1986年提出的，起初是针对非稳态可压流动的无迭代计算所建立的一种压力速度计算程序，后来在稳态问题的迭代计算中也较广泛地使用了该算法。

PISO算法与SIMPLE、SIMPLEC算法的不同之处在于：SIMPLE和SIMPLEC算法是两步算法，即一步预测和一步修正；而PISO算法增加了一个修正步，包含一个预测步和两个修正步，在完成了第一步修正得到（u，v，p）后寻求二次改进值，目的是使它们更好地同时满足动量方程和连续方程。PISO算法由于使用了预测—修正—再修正三步，从而可加快单个迭代步中的收敛速度。现将三个步骤介绍如下。

（1）预测步

使用与SIMPLE算法相同的方法，利用猜测的压力场p^*，求解动量离散方程式（1.2-18）与方程式（1.2-19），得到速度分量u^*与v^*。

（2）第一步修正

所得到的速度场（u^*，v^*）一般不满足连续方程，除非压力场p^*是准确的。现引入对SIMPLE的第一个修正步，该修正步给出一个速度场（u^**，v^**），使其满足连续方程。此处的修正公式与SIMPLE算法中的式（1.2-27）和式（1.2-28）完全一致，只不过考虑到在PISO算法还有第二个修正步，因此，使用不同的记法：

这组公式用于定义修正后的速度u^**与v^**：

就像在SIMPLE算法中一样，将式（1.2-68）与式（1.2-69）代入连续方程式（1.2-36），产生与式（1.2-37）具有相同系数和源项的压力修正方程。求解该方程，产生第一个压力修正值p'。一旦压力修正值已知，可通过式（1.2-68）与式（1.2-69）获得速度分量u^**与v^**。

（3）第二步修正

为了强化SIMPLE算法的计算，PISO要进行第二步的修正。u^**和v^**的动量离散方程是

注意这两式实际就是式（1.2-18）和式（1.2-19）。为引用方便，给出新的记号。

再次求解动量方程，可以得到两次修正的速度场（u^***，v^***）：

注意修正步中的求和项是用速度分量u^**和v^**来计算的。

现在，从式（1.2-72）中减去式（1.2-70），从式（1.2-73）中减去式（1.2-71），有

以上两式中，记号p''是压力的二次修正值。有了该记号，p^***可表示为

p^***=p^**+p′′ （1.2-76）

将u^***和v^***的表达式（1.2-72）和式（1.2-73）代入连续方程式（1.2-36），得到二次压力修正方程：

式中，a_i，j=a_i+1，j+a_i-1，j+a_i，j+1+a_i，j-1。读者可参考建立方程式（1.2-37）同样的过程，写出各系数如下：

下面对源项b'为何是式（1.2-78e）的形式作一简要分析和解释。

对比建立方程式（1.2-57）的过程，可以看出式（1.2-78e）中的各项，是因在u^***和v^***的表达式（1.2-74）和式（1.2-75）中存在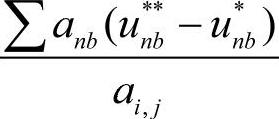和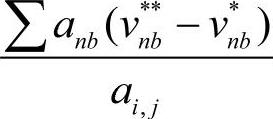项所导致的，而在u和v的表达式（1.2-30）和式（1.2-31）中没有这样的项。因此，式（1.2-37）不存在类似式（1.2-78e）中的各项。但式（1.2-37）存在另外一个源项，即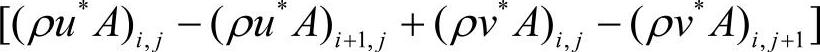，这是因速度u和v的表达式（1.2-74）和式（1.2-75）中的u^*与v^*项所导致的。按此推断，在式（1.2-78e）中也应该存在类似表达式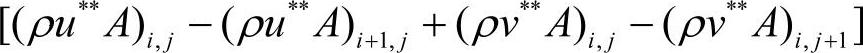。但是，由于u^**和v^**满足连续方程，因此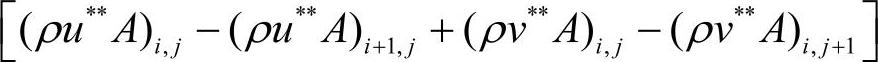为0。

现在，求解方程式（1.2-77），就可得到二次压力修正值p"。这样，通过下式就可得到二次修正的压力场：

p^***=p^**+p′′=p^*+p′+p′′ （1.2-79）

最后，求解方程式（1.2-74）与式（1.2-75），得到二次修正的速度场。

在瞬态问题的非迭代计算中，压力场p^***与速度场（u^***，v^***）一般认为是准确的。由于PISO算法要两次求解压力修正方程，因此，它需要额外的存储空间来计算二次压力修正方程中的源项。尽管该方法涉及较多的计算，但对比发现，它的计算速度很快，因此整体求解效率较高。对于瞬态问题，PISO算法有明显的优势；而对于稳态问题，选择SIMPLE或SIMPLEC算法会更合适。

4.SIMPLE系列算法的比较

SIMPLE算法是该系列算法的基础，目前在各种CFD软件中均提供这种算法。SIMPLE的各种改进算法，主要是提高了计算的收敛性，从而可缩短计算时间。

在SIMPLE算法中，压力修正值p'能够很好地满足速度修正的要求，但对压力修正不是十分理想。改进后的SIMPLER算法只用压力修正值p'来修正速度，另外构建一个更加有效的压力方程来产生“正确”的压力场。由于在推导SIMPLER算法的离散化压力方程时，没有任何项被忽略，因此所得到的压力场与速度场相适应。在SIMPLER算法中，正确的速度场将导致正确的压力场，而在SIMPLE算法中则不是这样。所以SIMPLER算法是在很高的效率下正确计算压力场的，这一点在求解动量方程时有明显优势。虽然SIMPLER算法的计算量比SIMPLE算法略高，但其收敛速度较快从而减少了计算时间。

SIMPLEC算法和PISO算法总体上与SIMPLER算法具有同样的计算效率，相互之间很难区分谁高谁低，对于不同类型的问题每种算法都有自己的优势。一般来讲，动量方程与标量方程（如温度方程）如果不是耦合在一起的，则PISO算法在收敛性方面显得很健壮，且效率较高。而在动量方程与标量方程耦合非常密切时，SIMPLEC和SIMPLER算法的效果可能更好些。

叶片泵设计简单算法的优化措施

相关推荐