叶片泵设计交错网格离散法：一种高效的数值计算方法

2023-06-26 理论教育版权反馈

【摘要】：从CFD历史发展的角度，基于交错网格的离散方法也是算法发展过程中的一个重要的基础。图1.2-1 交错网格的基本控制体积a）主控制体积 b）u控制体积 c）v控制体积图1.2-1中所示的均匀网格是向后错位的，因为u的速度uI，J的i位置到标量节点（I，J）的距离是-1/2δxu；同样，v速度vI，J的j位置到标量节点（I，J）的距离是-1/2δyv。

1.交错网格

在应用上述流程进行求解的时候，人们发现当压力呈棋盘状分布时该方法得到的计算结果存在严重的错误，也就是说压力和速度不能同时采用同一套网格布置，这就是采用交错网格的最初目的。因此，在早期的CFD软件中很多采用了交错网格的方法。从CFD历史发展的角度，基于交错网格的离散方法也是算法发展过程中的一个重要的基础。

所谓交错网格，就是将标量（如压力p、温度T和密度ρ等）在正常的网格节点上存储和计算，而将各速度分量分别在各坐标方向上错位半个网格后存储和计算，这样，错位后的网格中心将位于原控制体积的边界面处。所以，对于二维问题，就存在三套不同的网格系统，分别用于存储p、u和v；而对于三维问题，将用到四套网格系统，分别用于存储压力和三个速度分量。

二维流动计算的交错网格系统如图1.2-1所示，主控制体积为求解压力p的控制体积，称为标量控制体积或p控制体积，控制体积的节点P称为主节点或标量节点（见图1.2-1a）。速度u在主控制体积的东、西界面e和w上定义和存储，速度v在主控制体积的南、北界面s和n上定义和存储。u和v各自的控制体积则是分别以速度所在位置（界面e和界面n）为中心的，分别称为u控制体积和v控制体积，如图1.2-1b和图1.2-1c所示。可以看到，u控制体积和v控制体积是与主控制体积不一致的，u控制体积与主控制体积在x方向上有半个网格步长的错位，而v控制体积与主控制体积则在y方向上有半个步长的错位。

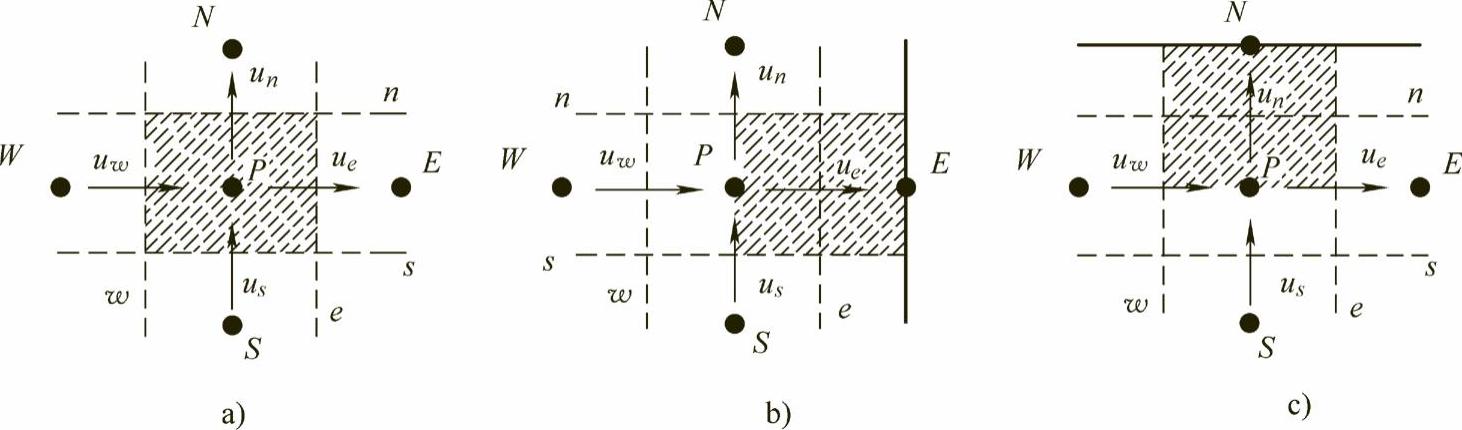
图1.2-1 交错网格的基本控制体积

a）主控制体积 b）u控制体积 c）v控制体积

图1.2-1中所示的均匀网格是向后错位的，因为u的速度u_I，J的i位置到标量节点（I，J）的距离是-1/2δx_u；同样，v速度v_I，J的j位置到标量节点（I，J）的距离是-1/2δy_v。当然，也可以选用向后两个错位的速度网格。

2.离散过程

采用了交错网格后，所得到的离散方程组仍然保持了一般的离散方程形式，但需注意，对于每个变量所选择的控制体积是不同的，如图1.2-2所示，在处理上要特别注意。取u方向的动量方程，其离散形式如下。

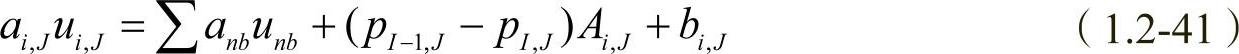
式中，A_i，J是u控制体积的东界面或西界面的面积，在二维问题中实际上是∆y，即

A_i，J=∆y=y_j+1-y_j （1.2-42）

式（1.2-41）中的b为u动量方程的源项部分（不包括压力在内）。对于稳态问题，有

b_i，J=S_uC∆V_u （1.2-43）

式（1.2-43）中的S_uC是对源项S_u线性化分解的结果，若S_u不随速度u而变化，则有S_uC≥S_u，S_uP=0。式（1.2-43）中的∆V_u是u控制体积的体积。式（1.2-41）中的压力梯度项已经按差分的方式进行了离散，差分使用了u控制体积边界上的两个节点的压力差。

在求和记号∑a_nbu_nb中所包含的E、W、N和S四个邻点是（i-1，J），（i+1，J），（i，J+1）和（i，J+1），它们的位置及主速度在图1.2-3中标出，图中阴影部分是u控制体积。图1.2-3中的u控制体积与图1.2-2中是一致的，这可从节点的编号看出，但是，图1.2-3中u控制体积的中心也用P来标记，其界面点也用e、w、n和s来标记，这里的标记与图1.2-2中的同名标记及系数a是由式（1.2-44）给定的。

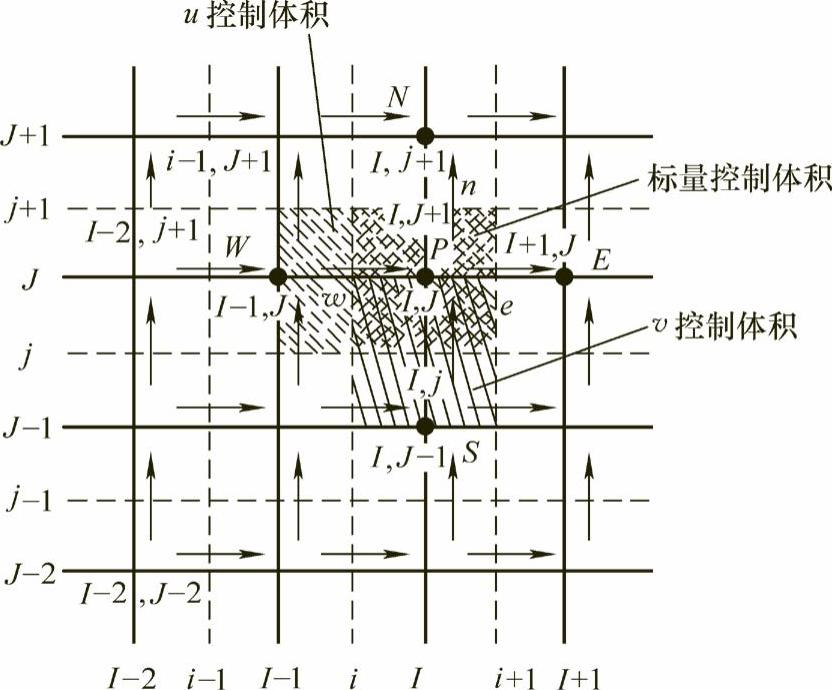
图1.2-2 交错网格

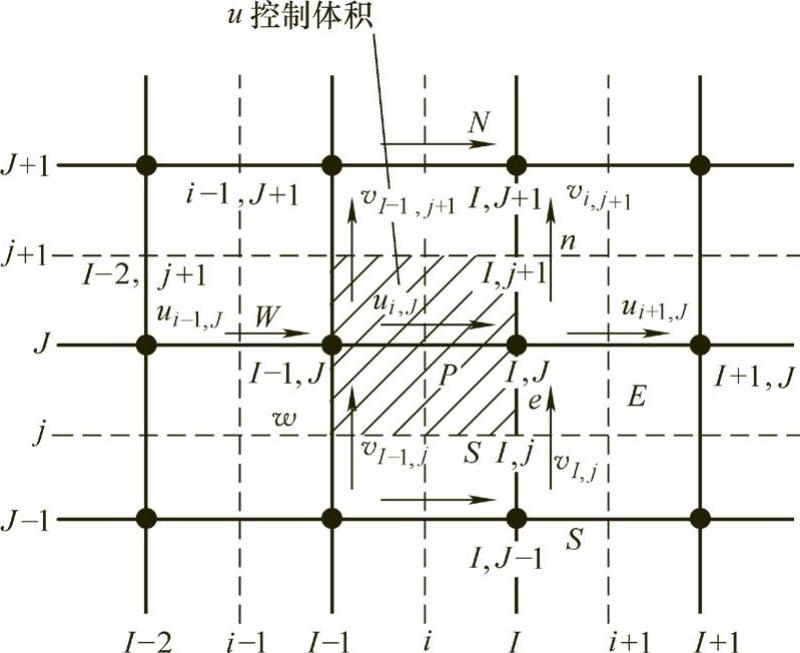
图1.2-3 u控制体积及其邻点的速度分量

系数a_nb取决于所采用的离散格式，在计算式中含有u控制体积界面上的对流质量流量F与扩散传导性D，在采用新编号系统下的计算公式为

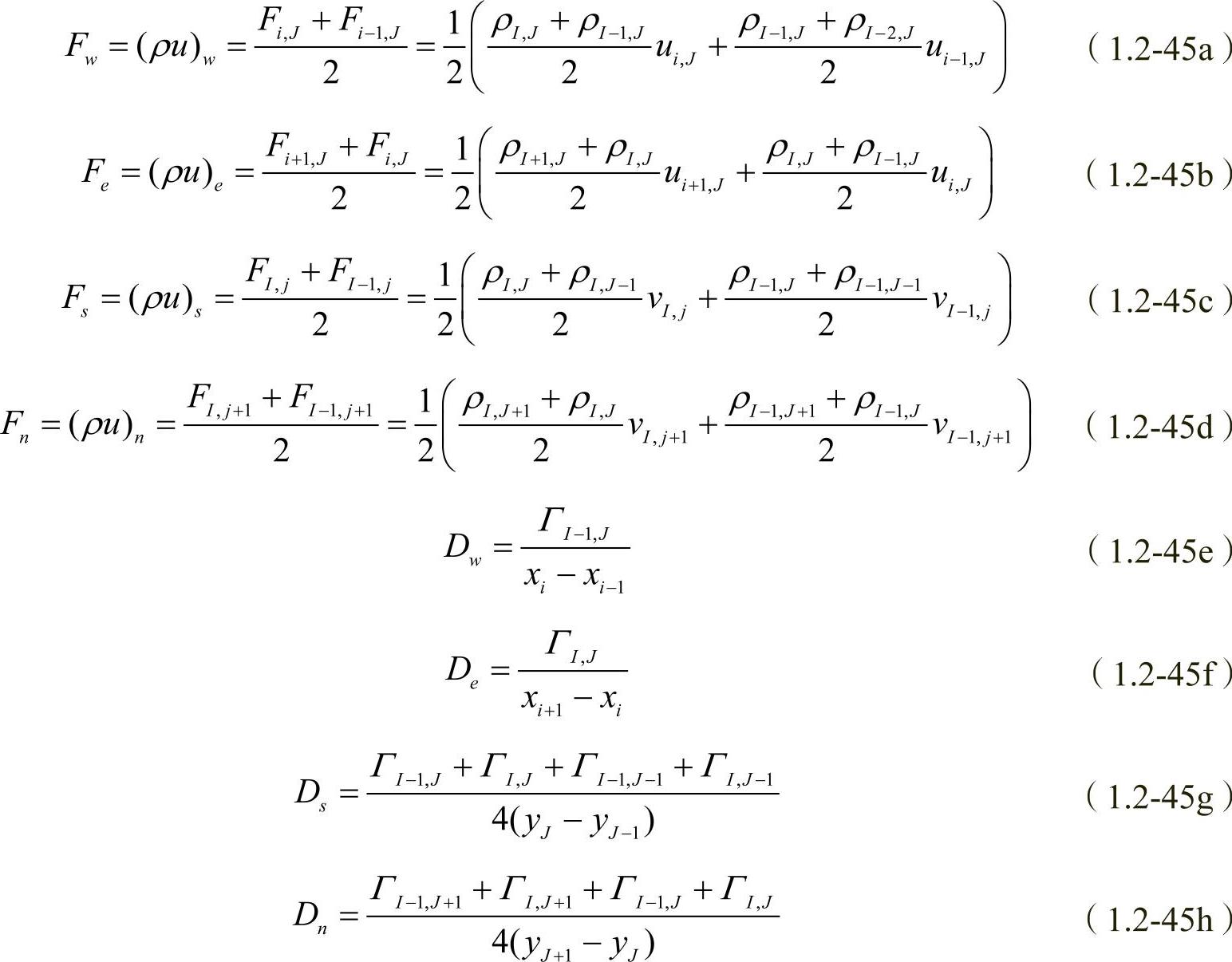
采用交错网格对动量方程离散时，涉及不同类别的控制体积，不同的物理量分别在各自相应的控制体积的节点上定义和存储。例如，密度是在标量控制体积的节点上存储的，如图1.2-3中的标量节点（I，J）；而速度分量却是在错位后的速度控制体积的节点上存储的，如图1.2-3中的速度节点（i，J）。这样就会出现这种情况：在速度节点处不存在密度值，而在标量节点处找不到速度值，当在某个确定位置处的某个复合物理量（见式（1.2-45）中的流通量F）同时需要该处的密度及速度时，要么找不到该处的密度，要么找不到该处的速度。为此，需要在计算过程中通过插值来解决。式（1.2-45）表明，标量（密度）及速度分量在u控制体积的界面上是不存在的，这时，根据周边的最近邻点的信息，使用二点或四点平均的办法来处理。

在每次迭代过程中，用于估计上述各表达式的速度分量u和速度分量v是上一次迭代后的数值（在首次迭代时是初始猜测值）。需要特殊说明的是，这些“猜测的”速度值u和v也用于计算方程式（1.2-41）中的系数a，但是，它们与式（1.2-41）中的待求u_i，J和u_nb是完全不同的。

还需要说明的是，式（1.2-45）中的线性插值是基于均匀网格的，若网格是不均匀的，应该将式（1.2-45）中的系数2和4等改为相应的网格长度或宽度值的组合。例如，对于不均匀网格上的F_w，按式（1.2-46）计算：

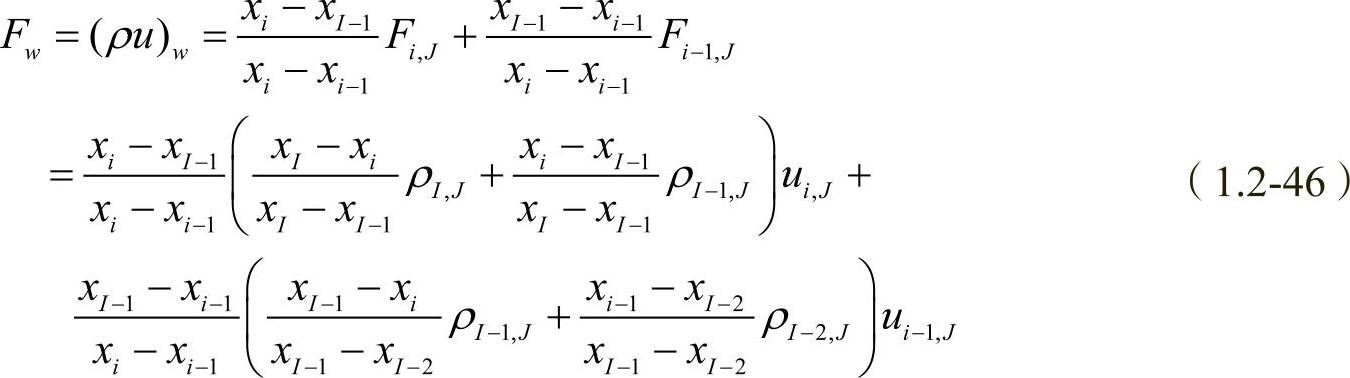
按上述同样的方式，可以写出在新的编号系统中，对于在位置（I，j）处的关于速度v_I，j的离散动量方程：

建立式（1.2-47）所使用的v控制体积表示在图1.2-4中。

在求和记号∑a_nbu_nb中所包含的4个邻点及其主速度也在图1.2-4中标出。在系数a_I，j和a_nb中，同样包含在v控制体积界面上的对流质量流量F与扩散传导性D，计算公式如下：

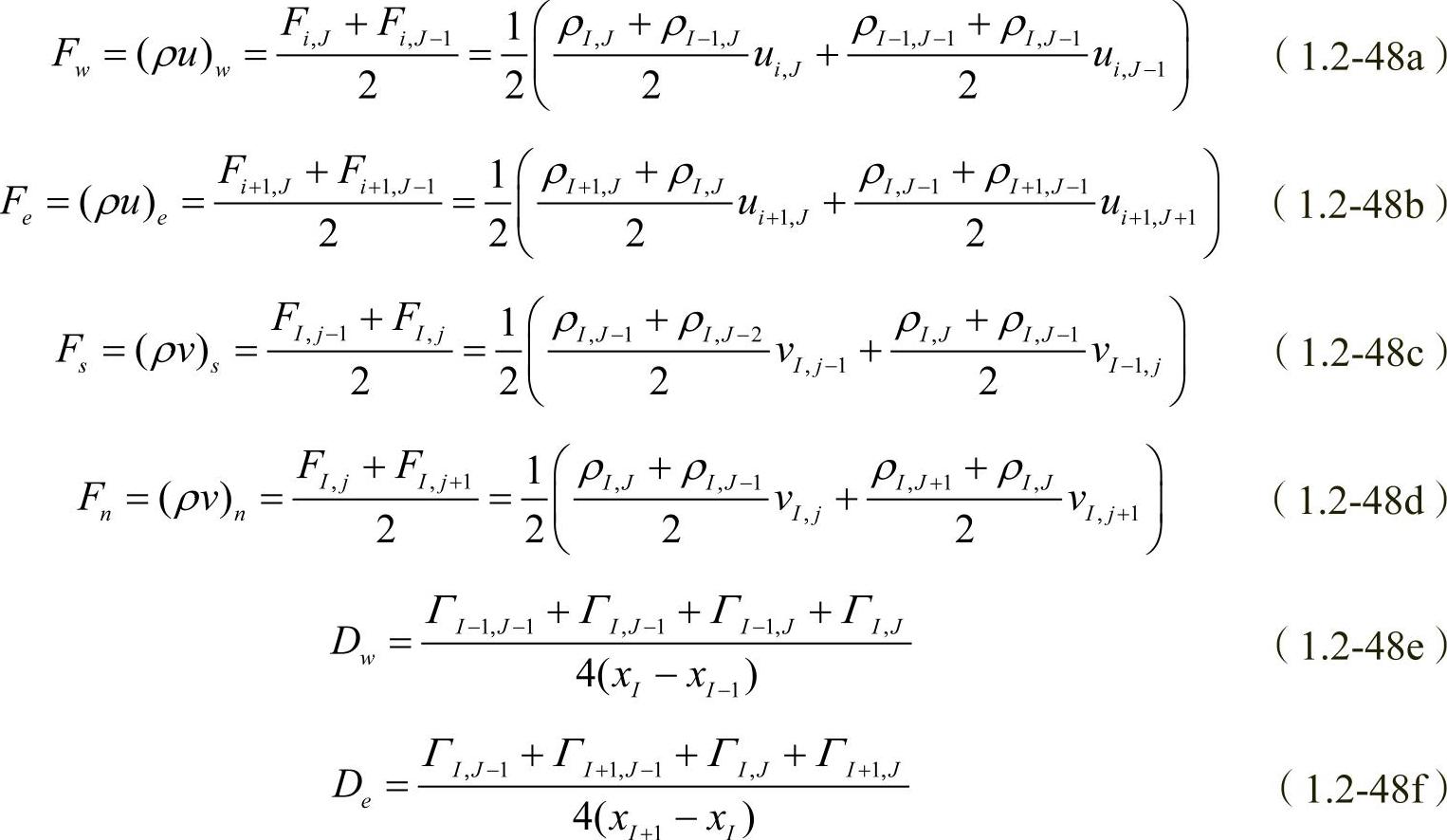
同样，在每个迭代层次上，用于估计上述各表达式的速度分量u和速度分量v均取上一次迭代后的数值（在首次迭代时是初始猜测值）。

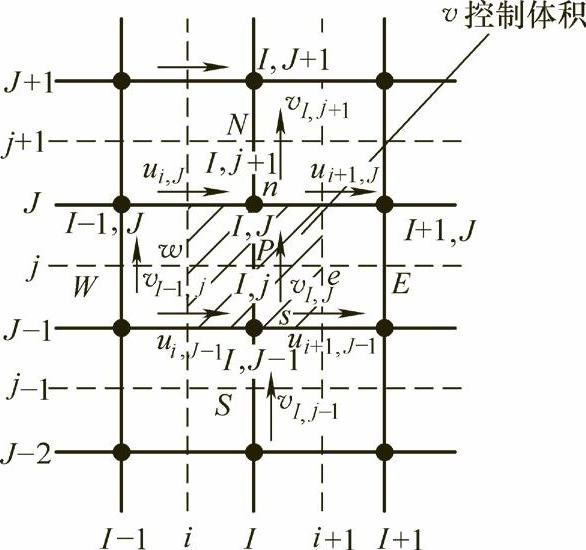
图1.2-4 v控制体积及其邻点的速度分量

给定一个压力场p，便可针对每个u控制体积和v控制体积写出式（1.2-41）和式（1.2-47）所示的动量方程的离散方程，并可以从中求解出速度场。如果压力场是正确的，所得到的速度场将满足连续方程。

叶片泵设计交错网格离散法：一种高效的数值计算方法

相关推荐