引入通用变量φ，将偏微分方程组式～为通用形式，并利用高斯定理在控制体积中离散，最终得到如下方程形式：式中：Гφ为通用扩散系数；Sφ表示源项。对时变项采用一阶差分格式离散，扩散通量采用超松弛校正方法计算，界面处梯度（▽φ）f由线性插值得到。于是单元面处通量可以表示为：式中：F f＝f；（φf）H为高阶部分，可以表示为：最终的方程离散形式如下：式中：；上标n为前一时间步长；下标P为当前控制体积。......
2023-06-26
叶片泵设计数值通用对流扩散方程的有限体积离散化
【摘要】：回代入原通量密度式得其中Fe=，令aE=∣DeA∣，有Je=p-aEE 类似可得Jw=aWW-p 对南北方向类似地有Jn=p-aNN Js=aSS-p 将以上四项回代入原式得aPP=aEE+aWW+aNN+aSS+b 对界面上函数及其导数采取特定的构造格式，即确定了系数A和B的具体形式，就可以获得最终的离散表达式。
利用有限体积法对上式进行离散
将源项线性化为：S=SC+SPϕP
重新整理上式得
令式（1.2-4）中Fe=（ρu）e∆y；Fw=（ρu）w∆y；Fn=（ρv）n∆x；Fs=（ρv）s∆x；
；
；
；
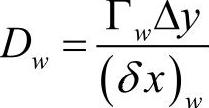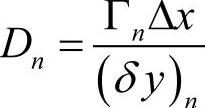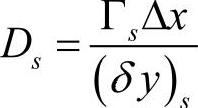；令P∆=F/D，表征对流与扩散作用的相对大小。
为获得通用的离散格式，从原通用式中提取出东西方向的通量密度
再除以D得
对式（1.2-6）取统一格式
这样，F、D与离散格式联系起来，只要选取恰当的格式，即确定了系数B和A的具体内容，就可以得到统一的离散方程。
回代入原通量密度式得
其中Fe=（DeP∆e），令aE=∣DeA（P∆e）∣，有
Je=（aE+Fe）ϕp-aEϕE （1.2-9）
类似可得
Jw=aWϕW-（aw-Fw）ϕp （1.2-10）
对南北方向类似地有
Jn=（aN+Fn）ϕp-aNϕN （1.2-11）
Js=aSϕS-（aS-Fs）ϕp （1.2-12）将以上四项回代入原式得
aPϕP=aEϕE+aWϕW+aNϕN+aSϕS+b （1.2-13）
对界面上函数及其导数采取特定的构造格式，即确定了系数A和B的具体形式，就可以获得最终的离散表达式。例如，由aE=∣DeA（P∆e）∣可以求得aE，同样可以获得aW、aN和aS。
上述方法同样适用于泵流动基本方程。对于流动方程，需将压力从源项中分离出，得到
Ai，J为东侧或西侧的面积，AI，j为南侧或北侧的面积。下标nb表示边界面，（i，j）和（I，J）为单元节点编号。
有关叶片泵设计数值模拟基础与应用的文章
- 详细阅读
-
叶片泵设计交错网格离散法：一种高效的数值计算详细阅读
从CFD历史发展的角度，基于交错网格的离散方法也是算法发展过程中的一个重要的基础。图1.2-1 交错网格的基本控制体积a）主控制体积 b）u控制体积 c）v控制体积图1.2-1中所示的均匀网格是向后错位的，因为u的速度uI，J的i位置到标量节点（I，J）的距离是-1/2δxu；同样，v速度vI，J的j位置到标量节点（I，J）的距离是-1/2δyv。......
2023-06-26
-
叶片泵设计数值数值计算方法概述详细阅读
用有限体积法导出的离散方程可以保证具有守恒特性，而且离散方程系数的物理意义明确，是目前流动与传热问题数值计算中应用最广泛的一种方法。有限体积法是目前流体流动和传热问题求解中最有效的数值计算方法，已得到广泛应用。......
2023-06-26
-
方程的离散求解方法详细阅读
图5-107控制体积法节点布局示意图5.5.3.2泥沙方程离散和求解悬移质输运方程离散和求解。悬沙输运方程和水流模型中的k、ε方程形式基本相同，只是在悬移质输运方程中多了一个下沉项，试算表明将下沉项作为源项比作为对流项更有利于求解的稳定。模型采用修正的QUICK 格式来离散悬沙输运方程的对流项，求解离散方程也采用ADI方法，相对于高阶格式所产生的离散方程的多余附加离散项采用显式离散，不存在求解困难。推移质输运方程的离散和求解。......
2023-06-22
-
变密度地下水溶质运移的数值方程及离散化处理详细阅读
考虑水头、密度与浓度三者相互影响的可溶混咸淡水中溶质运移问题，需要由两个偏微分方程描述，一是考虑密度随浓度不断变化的液体流动，二是溶质运移。可用一般的描述溶质运移的对流-弥散方程描述海水入侵模型中盐分的运移。地下水溶质运移方程的离散格式。在溶质运移方程空间离散化时，为克服对流项占优时引起的过量或者数值弥散的情况，在对流扩散方程中的对流项乘以一个适当的权因子，称为上游加权法。......
2023-06-25
-
叶片泵设计数值网格划分工具详细阅读
常用的网格划分工具有ICEM CFD、GridPro、Gridgen等。6）ICEM CFD系统还提供丰富的网格检查工具，便于用户对网格质量进行检查和修改。Gridgen曾是美国工程师和科学家采用的主流网格划分工具。......
2023-06-26
-
数值方程算法与验证详细阅读
Stone对全隐式差分方程提出了新的迭代解法——强隐式迭代解法，简称SIP方法。由于这种迭代方法利用解方程组对全部格点同时加以改进，迭代效率非常高，已经十分接近直接解法，因而也就更加有效。Trescott等所做的比较研究表明：对于复杂的实际问题，SIP方法明显优于其他的迭代方法。表5-3-1ADI算法时间为500天时浓度场计算结果表5-3-2SIP算法时间为500天时浓度场计算结果图5-3-6SIP算法实例验证图算例2作者对三维SIP算法也进行了编程验证，作为......
2023-06-25
-
浅水流动和物质输移扩散的数值模型优化详细阅读
但需要注意的是，连续方程式和运动方程式是相互耦合的。连续方程和运动方程的离散方程中，当采用线性化方法处理时，系数可由当前时刻的流场计算得到。第②、③步组成PISO循环，直至校正流速与预测流速之间的误差小于给定阈值。在PISO循环结束后，调用紊流模型和水质模型进行模拟，然后转入下一时间步的计算。......
2023-06-26
相关推荐