将出现的“Copy of Block 1”项改名为“Block2”。图5-54 添加计算域图5-55 分割计算域表面图5-56 设置好的计算域图5-57 重命名Block Face 4图5-58 输入新名称图5-59 取消边界层划分4.体网格的生成和检查在划分体网格前，选择[Continua]＞[Mesh 1]＞[Models]＞[Trimmer]项属性栏中的“Run Optimi-zer”项，体网格划分完成后进行网格质量的优化操作，如图5-60所示。......
2023-10-17
贴体网格生成方法及应用
【摘要】：本节介绍贴体网格生成方法。由于在数值求解方程组时，需要对计算域进行网格划分。图1.1-1 代数法插值方向示意图对于微分方法，拉普拉斯方程代表边值问题，可用来映像生成网格容易地导出其反函数为式中，，，。求解上述方程，即可获得网格数据。图1.1-2 单个叶轮通道内流和绕翼型外流网格
本节介绍贴体网格生成方法。
由于在数值求解方程组时，需要对计算域进行网格划分。对任意边界可以有两种网格生成方法：代数法和微分法。对于代数法，边界上的已知节点可以表示为
xb=xb（ξ，0），yb=yb（ξ，0） （1.1-1）
xt=xt（ξ，1），yt=yt（ξ，1） （1.1-2）
式中，x和h是边界点，采用连续插值方法，图1-1-1中内部节点坐标（x，y）可由边界点（x，h）插值获得
x（ξ，η）=xb（ξ）f1（η）+xt（ξ）f2（η） （1.1-3）
y（ξ，η）=yb（ξ）f1（η）+yt（ξ）f2（η） （1.1-4）
式中，f1（η）=1-η，f2（η）=η，根据不同的边界特征，可以选择从x或者h方向插值，从而获得理想的网格，如图1.1-1所示。
图1.1-1 代数法插值方向示意图
对于微分方法，拉普拉斯（Laplace）方程代表边值问题，可用来映像生成网格
容易地导出其反函数为
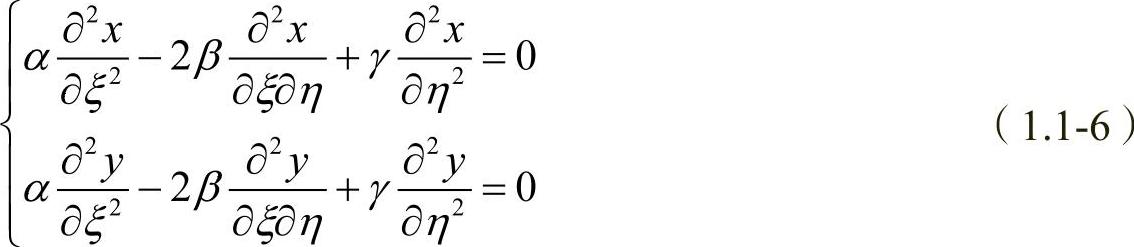
式中，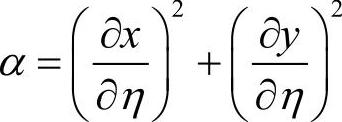
，
，
。
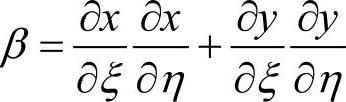求解上述方程，即可获得网格数据。根据边界特点，两种方法交互使用可以获得满意的网格，图1.1-2所示为单个叶轮通道内流和绕翼型外流的计算网格。
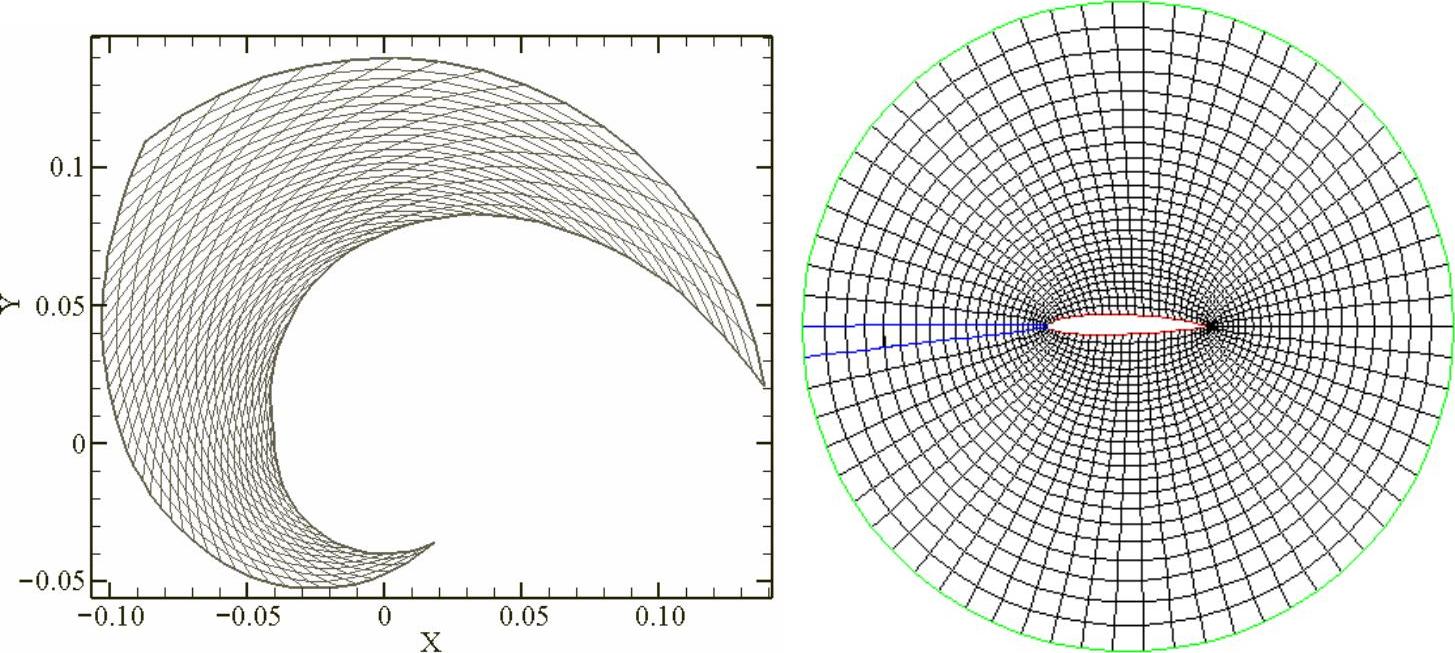
图1.1-2 单个叶轮通道内流和绕翼型外流网格
有关叶片泵设计数值模拟基础与应用的文章
- 详细阅读
-
网格划分方法与应用实例详细阅读
单击Mesh模块图标，进入网格划分模块，相应的工具条中显示出网格处理的快捷命令图标。设置Average Mesh Size为10，单位为mm。单击Apply按钮，生成一维梁单元，总计69个梁单元。单击Save按钮，保存文件。......
2023-10-27
-
多面体网格的优点及组合光顺成果详细阅读
图2-10 多面体网格的优点多面体模型对网格数量的依赖性比四面体小，只需四面体网格数的1/4即可保证计算精度，同时收敛速度、趋势更好于四面体网格。将两部分网格组合和光顺后，即成为图2-11所示的网格。......
2023-10-17
-
多面体的体积计算方法及应用详细阅读
2.已知一个正三棱柱的底面边长为3，高为4，求这个正三棱柱的体积.3.已知正四棱锥的底面边长为4，高为3.求这个正四棱锥的体积.4.旋转体的体积圆柱与棱柱的体积计算方法类似，都等于它的底面积S和高h的乘积，即V圆柱=Sh圆锥的体积也是同底等高的圆柱体积的，即其中，S是底面面积；h是圆锥的高.例4 有一堆相同规格的六角螺母毛坯，共重5.8kg.已知螺母的底面六边形边长是12mm，高是10mm，内孔直径是10mm，问约有毛坯多少个？......
2023-11-22
-
构建生成树的方法及步骤详细阅读
在介绍具体的生成树构建算法之前，首先作如下定义：ID。为了简便起见，省略根与成员之间的通信过程。第三次迭代时，子树1中的节点1向节点6发出连接请求，成功后节点6加入子树，至此所有节点已全部连接，生成树建立完毕。......
2023-07-02
- 详细阅读
-
STAR-CCM+流场计算：面网格生成和检查详细阅读
图5-31 建立Seed Point图5-32 包面网格数量4.重构操作由于重构操作只能针对一套网格进行操作，故需删除掉import网格。图5-33 删除import网格图5-34 确认删除图5-35 重构网格数量5.面网格检查和修复重构操作可以提升网格质量，但是不能保证所有的网格质量均较优。面网格检查采用图5-37中的标准。图5-36 质量较差的网格数量图5-37 面网格检查的标准点击“OK”按钮，出现图5-38所示的对话框。......
2023-10-17
-
生成收集物的方法及实践详细阅读
在Scripts文件夹内右键Create→C# Script，重命名CollectableSpawner，创建收集物生成器的逻辑脚本。图9-64聚光灯特效消失效果选中Hierarchy中的Collectable游戏对象，单击Inspector中的Apply按钮，应用之前的修改。图9-65应用修改然后，右键Collectable选择Delete删除游戏对象。图9-66将Collectable预制件指定到Collectable Prefab选项运行游戏，查看收集器生成器实际的创建收集物的效果，再控制维京人角色去拾取收集物，查看是否会在不同位置生成新的收集物。图9-67查看是否会在不同位置生成新的收集物......
2023-10-17
相关推荐