上式中系数矩阵的各分块子阵分别为经过派克变换后的磁链方程为这就是变换到d、q、0坐标系统的磁链方程。式中的Ld和Lq分别是定子的等效绕组dd和qq的电感系数，称为直轴同步电感和交轴同步电感。在目前采用的变换矩阵情况下，磁链方程中互感系数不可互易问题，只要将各量改为标么值并适当选取基准值即可克服。则最终得到的磁链方程为习惯上常将d、q、0系统中的电势方程和磁链方程合称为同步电机的基本方程，亦称派克方程。......
2023-06-15
机器人运动学中的T6和关节坐标系求解
【摘要】：用式（8-5）的T6可以表示手部的位置和方向，这样，六连杆机器人在它的活动范围内可以任意定位和定向。这样，变换T6可用下列矩阵表示：图8-7机器人手部机器人机构运动方程建立之后，如何根据已知（给定）的T6来求各关节坐标系的解，是机器人控制中更为重要的问题。
机器人机构由一系列关节连接起来的连杆所组成。把关节坐标系固连在机器人的每一个连杆上，可以用齐次变换来描述这些坐标系之间的相对位置和方向。
描述一个连杆相对于相邻连杆之间关系的齐次变换矩阵记为A矩阵。一个A矩阵是描述连杆机构坐标系之间相对平移和旋转的齐次变换。A1描述第1个连杆相对于参考坐标系的位姿，A2描述第2个连杆相对于第1个连杆坐标系的位姿。从而得到第2个连杆相对于参考坐标系的位姿可用下述矩阵表示：
类似地，A3描述第3个连杆相对于第2个连杆的位姿，则第3个连杆相对参考坐标系的位姿为
A1，A2，A3矩阵之积称为T3矩阵。以此类推，若有一个六连杆机器人，则有
一个六连杆机器人有6个自由度（每一连杆有一个自由度）。机器人最后一个构件（手部）有3个自由度用来确定其位置，3个自由度确定其方向。用式（8-5）的T6可以表示手部的位置和方向，这样，六连杆机器人在它的活动范围内可以任意定位和定向。图8-7所示为机器人手部，O0 X0 Y0 Z0为绝对坐标系，用3个单位向量n，o和a描述机器人的姿态。n表示法向矢量，其分量为T6坐标系的OX轴对绝对坐标系的3个方向余弦；o表示端面矢量，其分量为T6坐标系的OY轴对绝对坐标系的3个方向余弦；a表示逼近矢量，其分量为T6坐标系的OZ轴对绝对坐标系的3个方向余弦，表示手部执行器向被抓物运动的方向；p表示T6坐标系的原点在绝对坐标系中的位置矢量。这样，变换T6可用下列矩阵表示：
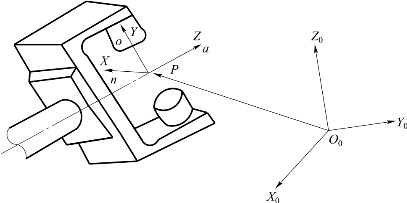
图8-7 机器人手部
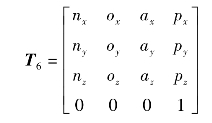
机器人机构运动方程建立之后，如何根据已知（给定）的T6来求各关节坐标系的解，是机器人控制中更为重要的问题。因此，这里要介绍机器人机构运动学方程的各种方法（Euler变换解、RPY变换解和SPH变换解等）。
有关工业机器人基础的文章
- 详细阅读
-
运动学与局部坐标系入门详细阅读
正的“应变”被定义为εii=Δu·ei不对下标进行求和式中，Δu是PSI单元两边之间的相对位移，Δu=uf-up；ei是局部坐标，下标i指三个局部坐标方向；二维单元只存在面内应变分量ε11、ε22，三维单元存在所有三个应变分量ε11、ε22和ε33。局部坐标系用三个正交方向e1、e2、e3来定义。在大位移分析中，局部坐标系随着所在管道的刚体运动而发生旋转。在小变形分析中，局部系统由PSI单元的初始几何构型来定义，并且在分析过程中保持不变。......
2023-06-24
-
机构运动分析及运动学方程求解详细阅读
10-1 如图10-19 所示机构中，椭圆规尺长AB=40 cm，曲柄长OC=20 cm，且AC=CB。如曲柄以匀角速度ω=πrad/s 绕O 轴转动，且已知AM=10 cm，求尺上M 点的运动方程和轨迹方程；t=0 和t=0.5 s 时的M 点的速度和加速度。图10-19题10-1图图10-20题10-2图10-3 如图10-21 所示，列车沿半径为R=800 m 的圆弧轨道做匀加速运动。图10-21题10-3图10-4 荡木用两条等长的钢索平行吊起，如图10-22 所示。......
2023-06-19
-
机器人关节伺服驱动及运动实现技巧详细阅读
机器人关节伺服驱动单元包括交流伺服电动机和交流伺服驱动器，如图5-5-7所示。在速度控制形式中，要求对交流伺服电动机在各种运行状态下的速度加以控制，以满足负载的工作要求，保证在定位时不产生振荡，保证焊接过程中焊接速度的稳定性。......
2023-06-26
-
运动关节的类型和特性详细阅读
表4.4不同类型的运动关节及其工作空间所有运动学由于其设计，也由于其加工区域几何结构，表现出不同的特定运动特性。图4.53不同类型的笛卡儿轴系统配置图4.54所示为塑料部件自动装置系统中的笛卡儿搬运系统。与完全标准的运动关节相比，这个市场在统计上更难表现出来。图4.57同一家制造商提供的不同关节臂运动关节当连接多个轴时，很明显，串行轴的精度，即连续连接的轴，对整个系统有重大影响。......
2023-06-15
-
坐标系统和计算网格详解详细阅读
5.5.4.3自适应计算网格生成河床及河岸的冲淤与其附近区域的水沙运动有十分密切关系，要求河道演变数学模型对河床及河岸附近流场和含沙场有较高的分辨率，采用固定网格会造成边岸有效网格呈现出阶梯状分布而降低河床和边岸附近的计算精度。......
2023-06-22
- 详细阅读
-
建筑施工中的坐标系统详细阅读
在进行工程总平面图设计时，为了便于计算和使用，建筑物的平面位置一般采用施工坐标系的坐标来表示。施工坐标系就是以建筑物的主轴线或平行于主轴线的直线为坐标轴而建立起来的坐标系统。为了计算放样数据的方便，施工控制网的坐标系统一般应与总平面图的施工坐标系统一致。施工坐标系统与测图坐标系统是有区别的。如图3-1 所示，x—O—y为测图坐标系，x′—O′—y′为施工坐标系。......
2023-06-29
相关推荐