机器人位姿表示优化方法

2023-06-26 理论教育版权反馈

【摘要】：在研究机器人的运动过程中，将涉及组成这一系统的各连杆之间，以及系统与对象之间的相互关系。展开上述旋转矩阵就得到欧拉角所表示的旋转矩阵。

机器人的机构可以看成一个由一系列关节连接起来的连杆所组成的多刚体系统。在研究机器人的运动过程中，将涉及组成这一系统的各连杆之间，以及系统与对象之间的相互关系。

1.直角坐标表示

1）刚体位姿表示

对于一个刚体，若给定了其上某一点的位置和该刚体在空间的姿态，则这个刚体在空间完全定位。

如图8-3所示，设O′为刚体上任意一点，OXYZ为参考坐标系，O′点在O系中的坐标可用一个列向量表示为

R0＝［x0y0z0］T

上式表示的即刚体上点O′在O系中的位置。若在刚体上建立一个坐标系O′X′Y′Z′，则刚体的方向可以由O′系坐标轴的方向表示，令n，o，a分别代表X′，Y′，Z′坐标轴方向的单位矢量，每个单位矢量在O系上的分量为O′系各坐标轴投影在O系上的方向余弦，于是刚体在参考坐标系内的方向可用由n，o，a三个矢量组合起来的三阶矩阵R来表示，即

R＝［n　o　a］

此矩阵为一旋转矩阵。

2）旋转矩阵的一般形式

刚体的运动可分解为旋转和平移，而运动的描述可以用上述O系和O′系的关系来表达，因此首先研究反映刚体定点旋转的坐标系变换矩阵——旋转矩阵，这是研究机器人运动姿态的基础。

设有两个共原点的坐标系OXAYA ZA和OXB YB ZB，如图8-4所示，｛B｝系可认为是｛A｝系绕定点O旋转而成的。若空间有一点P，该点在｛A｝系内的坐标为［xAyAzA］T，在｛B｝系内的坐标为［xByBzB］T，若以｛A｝系为参考坐标系，根据投影关系，P点从｛B｝系变换到｛A｝系的坐标变换关系为

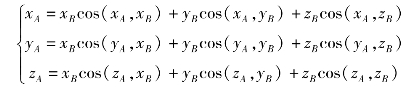
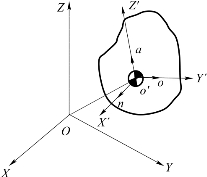
pagenumber_ebook=322,pagenumber_book=312

图8-3　刚体位置和方向

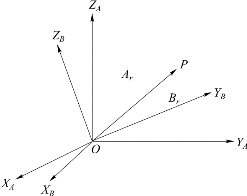
pagenumber_ebook=322,pagenumber_book=312

图8-4　坐标系的旋转

这一关系可以用矩阵表达为

式中

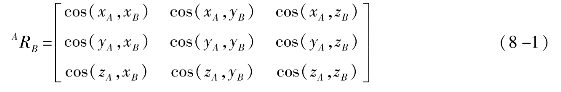
pagenumber_ebook=323,pagenumber_book=313

2.欧拉角表示

所谓欧拉角是对绕不同坐标轴旋转的转角规定的一个序列，由于欧拉角的不同取法，旋转矩阵有不同的表达式。它们均可描述刚体相对于固定参考系的姿态。

如图8-5所示，｛B｝系对｛A｝系的姿态可以认为是通过绕ZA轴旋转φ角，然后绕新的Y1轴旋转θ角，最后绕新的Z2（ZB）轴旋转ψ角而得，因此用三个欧拉角φ，θ，ψ表示的旋转矩阵为

此式右边表示三次连续旋转的旋转矩阵。反之，若右边三个矩阵从右向左连乘，表示各次旋转均绕参考系｛A｝的有关轴进行，即首先绕XA轴旋转ψ角，再绕YA轴旋转θ角，最后再绕ZA轴旋转φ角，如此可同样得到｛B｝系对｛A｝系的姿态。

可见多个旋转矩阵连乘时，次序不同则含义不同，右乘的次序说明连续绕新的坐标轴旋转，而左乘的次序则表明绕固定参考系坐标轴依次旋转。展开上述旋转矩阵就得到欧拉角所表示的旋转矩阵。

另一种表示旋转的欧拉角称为侧滚（roll）、俯仰（pitch）、偏航（yaw），主要用于航空工程中分析飞行器的运动，如图8-6所示。这三个角是导航专业中常用的，｛B｝系开始时与｛A｝系重合，侧滚是绕ZA轴旋转φ角，俯仰是绕YA轴旋转θ角，偏航是绕XA轴旋转ψ角，规定旋转次序为先绕XA轴，再绕YA轴，最后绕ZA轴，则三次旋转矩阵为

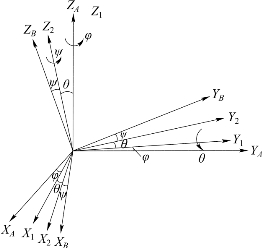
pagenumber_ebook=323,pagenumber_book=313

图8-5　欧拉角旋转变换

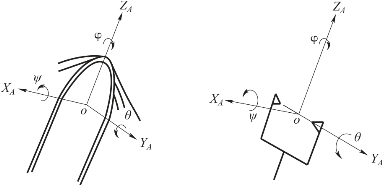
pagenumber_ebook=323,pagenumber_book=313

图8-6　RPY旋转变换

pagenumber_ebook=324,pagenumber_book=314

机器人位姿表示优化方法

相关推荐