图6-23 高速火焰喷涂的水冷炉壁管能源工业热喷涂技术最典型的应用是大中型火力发电厂锅炉水冷炉壁、过热气管、再热器管和省煤气器管的表面防护。图6-24 高速火焰喷涂排粉风机叶轮耐磨涂层3.在核能工业中的应用热喷涂涂层在核能工业中有着重要的用途。该技术成功地解决了原子能反应堆一次回路钴60放射性污染问题，已经在核工业中得到成功应用。......
2025-09-29
实现创新的冲突矩阵应用技巧
【摘要】：冲突矩阵是一个40行40列的矩阵，其中第一行或第一列为按顺序排列的39个通用工程参数序号，见表2-1。矩阵中的行所代表的工程参数是希望改善的一方，列所代表的工程参数为冲突可能引起恶化的一方。表2－1冲突矩阵表2.利用冲突矩阵实现创新的步骤定义待设计系统的名称。在冲突矩阵中由冲突双方确定相应的矩阵元素。找到、评价并完善概念设计及后续的设计。
1.冲突矩阵
经过多年的研究、分析和比较，Altshuller提出了冲突矩阵。该矩阵将描述技术冲突的39个通用工程参数与40条发明原理建立了对应关系，很好地解决了设计过程中选择发明原理的难题。
冲突矩阵是一个40行40列的矩阵，其中第一行或第一列为按顺序排列的39个通用工程参数序号，见表2-1。除了第一行和第一列外，其余39行39列形成一个矩阵，矩阵中数字表示40条发明原理中推荐采用的原理序号。矩阵中的行所代表的工程参数是希望改善的一方，列所代表的工程参数为冲突可能引起恶化的一方。
表2－1 冲突矩阵表
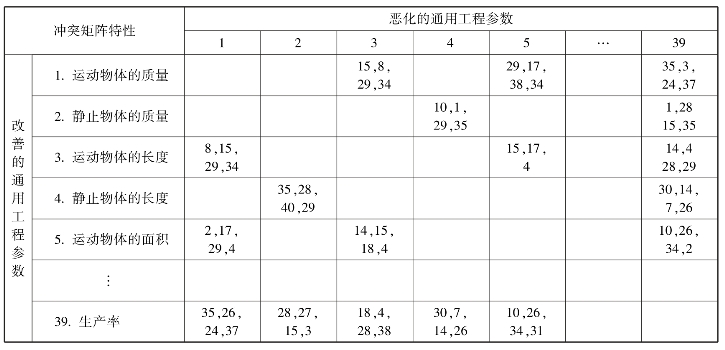
2.利用冲突矩阵实现创新的步骤
（1）定义待设计系统的名称。
（2）确定待设计系统的主要功能。
（3）列出待设计系统的关键子系统、各种辅助功能。(https://www.chuimin.cn)
（4）对待设计系统的操作进行描述。
（5）确定待设计系统应改善的特性、应该消除的特性。
（6）将涉及的参数要按标准的39个工程参数重新描述。
（7）对技术冲突进行描述：如果某一工程参数要得到改善，将导致哪些参数恶化。
（8）对技术冲突进行另一种描述：假如降低参数恶化的程度，要改善参数将被削弱，或另一恶化参数将被加强。
（9）在冲突矩阵中由冲突双方确定相应的矩阵元素。
（10）由上述元素确定可用发明原理。
（11）将所确定的原理应用于设计者的问题。
（12）找到、评价并完善概念设计及后续的设计。
相关文章
- 详细阅读
-
坐标变换指令：实现精准定位的技巧详细阅读
极坐标编程可通过指令G16生效、指令G15撤销。图4.1-4 极坐标编程图4.1-5 镜像加工CNC的镜像加工，一般可以通过如下三种方式选择：1）利用CNC的M指令和PMC程序设计，使对应的坐标轴进入镜像加工。2）镜像加工生效时，指令G02/G03的圆弧插补方向、指令G41/G42的半径补偿方向、指令G68/G69的坐标旋转方向均将被互换。图4.1-8 圆弧插补的比例缩放图4.1-9 坐标旋转4.坐标旋转对于图4.1-9所示的某些围绕中心旋转得到的特殊轮廓加工，可使用坐标旋转功能简化编程。......
2025-09-29
-
实现动画效果的方法与技巧详细阅读
WinCC flexible有非常强大的动画功能，几乎可以对每一个画面设置动画功能。下面我们通过一个简单的例子演示动画功能的实现方法。新建用于控制小车移动的Short型变量tag1。在画面一中，通过简单对象“矩形”和“圆”画出一个小车的示意图。图7-12 组合的属性对话框在画面中再生成一个IO域，用来显示变量tag1的值。这样画面的组态就完成了。图7-13 IO域的外观动画设置......
2025-09-29
-
智能技术在果蔬包装中的创新应用详细阅读
但是，对于活性包装和智能包装这两大类包装系统目前还没有统一和明确的定义。图5-1果蔬的智能包装示意与在大多数科技领域中一样，纳米技术有望在活性和智能包装方面发挥重要作用。相关立法和成本也可能对智能包装的实际商业应用有较大影响。运输过程中机械性损伤是造成番茄品质下降的主要原因。活性包装和智能包装可能是这类产品重要的应用领域，有助于提高产品的保质期，监测产品的质量和安全性。......
2025-09-29
- 详细阅读
-
印制电池：碳-锌制造技术的创新应用详细阅读
BlueSpark公司基于碳-锌制造的，厚度为500μm的印制电池工作电压为1.5V，可以提供超过1mA的峰值电流。锂离子技术目前能够提供最佳的能量密度，并且正在主导着移动电源市场。该项目的目标是通过只有使用印制技术才能实现的方法，在设备上直接印制一个完整的锂离子电池。......
2025-09-29
-
专业能力素质达成矩阵设计与应用详细阅读
课程体系建立后，需要对各门课程的能力素质达成情况进行考查。将课程i的j目标的达成度记为Ti，j，则该课程对专业能力素质培养的总达成度为所有课程对第j项能力素质目标的总达成度为式中，K为开设课程的数量。专业能力素质达成度Q表示为或表示为上述两式具有不同的含义。专业开设的课程和能力素质目标共同构成了专业能力素质达成矩阵，即表3-1所示为其表格形式。......
2025-09-29
- 详细阅读
相关推荐