电波传播特性分析

2023-06-26 理论教育版权反馈

【摘要】：图10.2电波的反射直射波TR 的行程与反射波TPR 的行程差为Δr=r2-r1假设d h1，h2则所以设地面反射波的反射系数为ρ。图10.3电波传播的刃形阻挡图10.4路径余隙造成的阻挡效应如图10.5所示，满足的所有点Q 的集合叫第n 菲涅尔区。图10.5电波传播的菲涅尔区第n菲涅尔区边界上的某个点P 到T、R 连线的距离Fn叫第n 菲涅尔区半径。

1.电波的自由空间传播

所谓自由空间是指理想的电磁波传播环境。自由空间传播损耗的实质是能量因电波扩散而损失，其基本特点是接收电平与距离的平方成反比，与频率的平方成反比。

图10.1中T 为发射天线端，R 为接收天线端，T 和R 相距d（单位：km）。若发送端的发射功率为Pt，采用无方向性天线时距离d 处的球面面积为4πd 2，因此在接收天线的位置上，每单位面积上的功率为。如果接收端用的也是无方向性接收天线，根据天线理论，此天线的有效面积是。因此接收端功率为

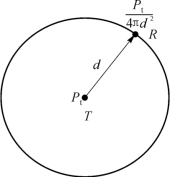
pagenumber_ebook=288,pagenumber_book=275

图10.1　自由空间传播

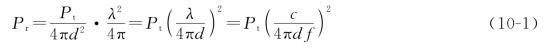
pagenumber_ebook=289,pagenumber_book=276

路径损耗为

其中，f（单位：GHz）为信号的频率，c为光速，λ为信号波长。自由空间损耗写成分贝值为

2.电波传播的几何模型

电波传播的几何模型是分析电波传播特性的基本方法，几何模型多用在传播径数不多的情况，如数字微波信道、移动卫星信道等，其分析是基于电波的直线传播特性及电波的反射、绕射、折射。

（1）电波的反射

电波的反射如图10.2所示。

pagenumber_ebook=289,pagenumber_book=276

图10.2　电波的反射

直射波TR 的行程与反射波TPR 的行程差为

Δr=r2-r1

假设d ≫h1，h2则

所以

设地面反射波的反射系数为ρ。反射波与直射波之间存在着相位差，其中行程差引起的相位差为，另外反射将引起π相移。接收到的合成电场的强度为

Et是发送的电场强度。α（r1）是距离r1引起的幅度损耗是距离r2引起的幅度损耗。因为r1≈r2≈d，所以

于是

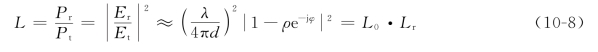
pagenumber_ebook=290,pagenumber_book=277

其中，反映距离因素造成的衰减（自由空间损耗），反映反射因素附加的衰减。当行程差远远小于波长（如天线较低、距离d 很大或者频率低）时

考虑两个极端：ρ=0时，为自由空间情形，接收信号的衰减同距离的平方成正比；反射最强时ρ=1，，信号衰减同距离的4次方成正比，同时与天线高度的平方成反比。ρ=1时的模型也叫“平面大地模型”。一般来说，传播损耗与距离的n次方成正比，即L ∝d n ，n通常是界于2～4之间的一个实数，叫传播损耗指数。

平面大地模型表示为分贝值为

（2）电波的阻挡与绕射

如图10.3所示，当T 和R 之间出现刃形障碍物时，它有可能对电波产生阻挡作用。阻挡引起的损耗与余隙的大小有关，路径余隙为障碍物定点至TR 连线的垂直距离。根据电磁波绕射行为，如果余隙（F1为第一菲涅尔区半径）时，阻挡引起的损耗正好是0 dB，也即路径损耗正好是自由空间损耗，所以h0叫自由空间余隙。若余隙大于h0，路径损耗随hc的增加略有波动，最终稳定在自由空间损耗上。若余隙小于h0，那么随着hc的减小路径损耗急剧增加。图10.4所示为路径余隙与阻挡损耗之间的关系。

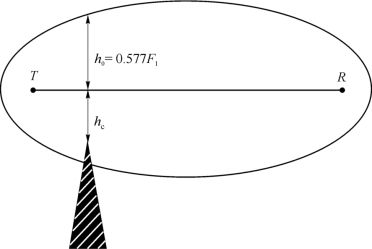
pagenumber_ebook=290,pagenumber_book=277

图10.3　电波传播的刃形阻挡

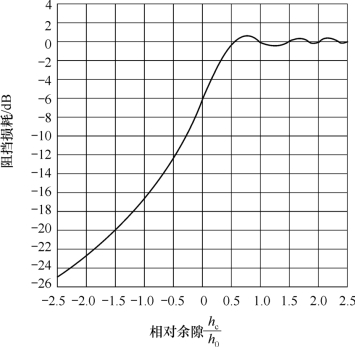
pagenumber_ebook=290,pagenumber_book=277

图10.4　路径余隙造成的阻挡效应

如图10.5所示，满足（n 为整数）的所有点Q 的集合叫第n 菲涅尔区。菲涅尔区的形状是一个椭球体。

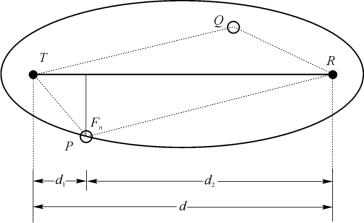
pagenumber_ebook=291,pagenumber_book=278

图10.5　电波传播的菲涅尔区

第n菲涅尔区边界上的某个点P 到T、R 连线的距离Fn叫第n 菲涅尔区半径。当P 处于图中的正中处时，Fn达到最大值Fnmax，叫第n菲涅尔区的最大半径。

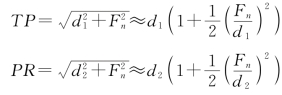
pagenumber_ebook=291,pagenumber_book=278

因为在边界上满足，所以有

（3）大气折射与等效地球半径

大气密度的不均匀导致电波弯曲。从电波的角度看，似乎是地球的曲率发生了变化。以电波为直线时看到的“等效地球半径”为Re=KR0，系数叫“等效地球半径系数”，K 的典型值为。由于大气折射的因素，通常情况下，最大视距会更大一些。

（4）电波传播的路径损耗预测

在实际环境中，电波的传播模型很复杂，研究者们提出了若干经验模型来预测传播损耗，典型的有Okumura模型、Hata模型和Lee模型等。利用这些模型可以估算移动通信系统中无线电波在城市、郊区、农村的路径损耗。

这里主要介绍Hata模型。Hata模型是一种被广泛使用的传播模型，适用于宏蜂窝（小区半径大于1 km）系统的路径损耗预测，根据应用频率不同，Hata模型分为两类。

1）Okumura-Hata模型

适用频率范围为150～1 500 MHz，主要用于900 MHz频段，该模型以市区传播损耗为标准，并根据具体地形做不同的修正。市区模型的经验公式如下：

式（10-12）中，f 是系统工作频率，单位为MHz；hte是基站天线高度，单位为m，有效天线高度为30～200 m 之间；hre是移动台天线高度，单位为m，移动台有效天线高度为1～10 m 之间；d 是发射机与接收机之间的距离，大于1 km；a（hre）是移动天线修正因子，单位为d B，其数值取决于环境。

对于中小城市

a(hre)=(1.1lg fc-0.7)hre-(1.56lg fc-0.8)

对于大城市

a(hre)=3.2(lg 11.75hre)2-4.79 fc≥300 MHz

a(hre)=8.29(lg 1.54hre)2-1.1 fc＜300 MHz

对于郊区，该模型修正为

但是应该看到，上述模型只是一个经验公式，具体的应用还必须通过实际测量来确定，包括不同环境下的修正因子。

2）COST-231 Hata模型

由于式（10-12）的适用频率范围不适合于PCS（1 900 MHz）频段，EURO-COST 组成的COST-231工作委员会提出了COST-231 Hata模型，该模型使用频率范围为1 500～2 000 MHz，基站半径范围1～20 km。

式（10-14）中，CM为大城市中心校正因子，市中心的CM=3 dB，在中等城市和郊区的CM=0。

3.电波的多径传播和衰落

除了路径损耗外，电波在传播中，可能受到长期慢衰落和短期快衰落的影响，如图10.6所示。

pagenumber_ebook=292,pagenumber_book=279

图10.6　电波传播的长期衰落与短期衰落示意图

（1）电波传播的长期慢衰落

长期慢衰落是由传播路径上的固定障碍物（如建筑物、山丘、树林等）的阴影引起的，因此也称为阴影衰落或大尺度衰落。阴影引起的信号衰落是缓慢的，且衰落速率与工作频率无关，只与周围地形、地物的分布、高度和物体的移动速度有关。

长期衰落一般表示为电波传播距离的平均损耗（dB）加一个正态对数分量，其表达式为

其中，Ls是距离因素造成的电波损耗；Xσ是满足正态分布的随机变量，其均值为0，方差为σ2，移动通信环境中σ2 的典型值为8～10 dB。

（2）电波传播的短期快衰落

由于电波具有反射、折射、绕射的特性，因此接收端接收到的电波信号可能是从发送端发送的电波经过反射、折射、绕射的信号的叠加，即接收信号是发送信号经过多种传播途径的叠加信号。此外，反射、折射、绕射物体的位置可能随时间变化，则接收到的多径信号也可能随时间变化，当电波频率较高时，微小的距离变化导致多径叠加信号强度的快速变化，即接收端接收到的信号具有快速时变特性，这种特性称为短期快衰落或小尺度衰落。无线通信中的电波传播经常受到这种多径时变的影响。

考察信道对发送信号的影响，发送信号一般可以表示成

假设存在多条传播路径，且与每条路径有关的是时变的传播时延和衰减因子，则接收到的带通信号为

式（10-17）中，αn（t）是第n条传播路径的时变衰减因子，τn（t）是第n条传播路径的时变传播时延，sl（t）是发送信号的等效低通信号。可以看出，接收信号的等效低通信号为

而等效低通信道可用如下的时变冲激响应表示

对于某些信道，把接收信号看成由连续多径分量组成的更合适，其等效低通信道为

c(τ;t)=α(τ;t)e-j2πf cτ

此时的接收信号为

1）信道的时变性

发送信号经过无线信道时，受时变因素的影响，如式（10-19）中所示，各传播路径的衰减幅度、传播时延随时间变化，这种变化因素可由周围反射物、折射物、绕射物的移动或其他因素引起。如此，发送信号在前一时刻经受的衰落与下一时刻经受的衰落可能不同，即信道条件随时间变化，造成了时变性。

描述信道时变快慢特性采用信道的相干时间td或多普勒频移fd。当发送信号的码元时间Ts与多普勒频移fd的乘积远小于1，即fdTs≪1时，在每个码元时间内，信道的时变因素可以忽略，称此时发送信号经历慢衰落；当发送信号的码元时间Ts与多普勒频移fd的乘积与1可比时，此时每个码元时间内，信号的时变因素不可以忽略，发送信号经历快衰落。通常，信道的时变性与信号的发送速率相比慢得多，因此实际系统中相对于一个码元时间内往往可以看成是信道时不变的。

多普勒频移是根据电波传播的多普勒效应来计算的。多普勒效应是为纪念Christian Doppler而命名的，他于1842年首先提出了这一理论。他认为声波频率在声源移向观察者时会变高，而在声源远离观察者时会变低。一个常被使用的例子是火车，当火车接近观察者时，其汽鸣声会比平常更刺耳。观测者可以在火车经过时听出刺耳声的变化。同样的情况还有警车的警报声和赛车的发动机声。

把声波视为有规律间隔发射的脉冲，可以想象若你每走一步，便发射了一个脉冲，那么在你之前的每一个脉冲都比你站立不动时更接近你，而在你后面的声源则比原来不动时远了一步，即在你之前的脉冲频率比平常变高，而在你之后的脉冲频率比平常变低了。

多普勒效应不仅仅适用于声波，它也适用于所有类型的波，包括无线电和光波等。当移动体在x 轴上以速度v 移动时，引起多普勒（Doppler）频率漂移。用一个平面波表示稳定扩散事件，假定x-y 平面是平面场，如图10.7所示，此时，多普勒效应引起的多普勒频移可表示为

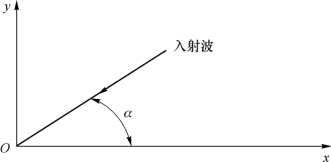
pagenumber_ebook=294,pagenumber_book=281

图10.7　入射波和移动方向

式（10-21）中，v为移动速度，λ为波长，α为入射波与移动台移动方向之间的夹角，为最大多普勒频移。

2）信道的多径特性

现在来观察一个两径的信道的例子。例如，α0=α1=1，τ0（t）=0，τ1（t）=1μs，fc=1 MHz，则由式（10-19）可以得到等效低通信道为

c(τ;t)=δ(τ)+δ(τ-τ1)

其傅氏变换为

C(f;t)=1+e-j2πfτ1=2cos(πfτ1)e-jπfτ1

图10.8所示为上述两径信道的幅频响应。

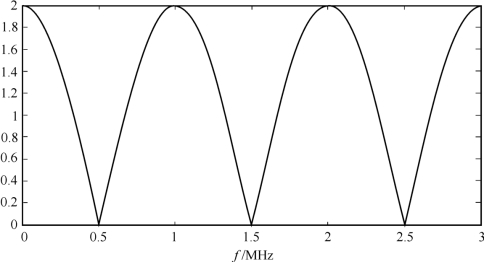
pagenumber_ebook=294,pagenumber_book=281

图10.8　两径信道的幅频响应示意图

从图10.8中可以看到，当发送信号的频带宽度大于0.5 MHz时，信号经过信道时会引起严重的频率选择性衰落，即信号的某些频率分量被严重衰减，某些分量被放大。这种频率选择性衰落对宽带信号传输十分不利，如果没有采取措施进行补偿，则接收到的信号具有严重的失真。

多径传输导致信道对输入信号具有频率选择性，表征信道的这种特征经常用信道的多径时延扩展τm这个参数来描述。当发送信号的带宽B 与多径时延扩展τm的乘积远小于1，即Bτm≪1时，信号的带宽相对于多径的选择性带宽而言很小，通常称此时信号经历平衰落；当发送信号的带宽B 与多径时延扩展τm的乘积与1可比时，发送信号的带宽与多径的选择性带宽具有可比性，通常称此时信号经历频率选择性衰落。

例如，地面微波中继通信信道可以等效成一个两径模型，其中一径是直射路径分量（LOS），另外一径来自周围地形的反射。1979年，Rummler开发出一种基于信道测量的两径模型，该测量是在6 GHz频带的典型LOS链路上进行的，测量得到的信道转移函数可以建模为

式（10-22）中，α为总衰减参数，其分布可用对数正态分布来描述；β为由多径分量引起的形状参数，其分布具有（1-β）2.3的形式；f0为衰落最小的频率；τ0为直射路径与反射路径的时延差，其典型值为6.3 ns。

对于β＞0.5，-20lgα的均值为25 dB，标准偏差为5 dB；对于较小的β值，-20lgα的均值为15 dB，标准偏差为5 dB。

3）信道衰落的分布

由式（10-19）所示，信道的等效包络基本反映了接收信号的包络，即接收信号的起伏特性。当多径数很大，且每径的衰减和时延随机时，根据大数定理，信道可以等效成一个复高斯的随机过程，此时由于复高斯的幅度呈瑞利分布（Rayleigh），通常称为瑞利衰落信道；当多径结构中具有明显的直射路径或有明显的强径时，信道可以等效成一个正弦波加复高斯的随机过程，此时信道的幅度为莱斯分布，称为莱斯（Rice）衰落信道；另外一种表征通过多径信道传输的信号起伏的统计特性的分布是Nakagami分布。

4）中断率和衰落余量

通信系统的误码率是信噪比的函数，在衰落信道中信噪比是时变的，因此瞬时误码率也是时变的。当信噪比低于某个限值r0时，信道将处于不能满足要求的状态，称为“中断”。中断出现的时间比率叫作中断率（Outage Rate），或者叫瞬断率。通常的计算方式是

Pout=Pr(SNR＜r0)

其中，Pr（A）表示事件A 发生的概率。假设接收功率为Pmin时恰好Pe=1×10-3，则中断率为概率

Pout=Pr(P＜Pmin)

这里P 是接收信道功率。由于衰落的原因，P 是随机变量。

为了保证中断率低于一定的指标，平时的接收电平应该比最少需要的接收功率留出有些余量。留的余量越多，中断率就越小。

电波传播特性分析

相关推荐