连接功能的数学描述：深入探讨

2025-09-29 理论教育版权反馈

【摘要】：通常交换网络内部的通道被称为“连接”，建立内部通道就是建立连接，拆除内部通道就是拆除连接。下面分别从连接集合和连接函数出发来讨论。连接函数实际上也反映了入线编号构成的数组和出线编号构成的数组之间对应的置换关系或排列关系。所以连接函数也被称为置换函数或排列函数。图4.15连接函数δ=x1x0x2的图形表示

交换的基本功能是在任意的入线和出线之间建立连接，或者说是将入线上的信息分发到出线上去，当然，按照不同交换方式的要求，可以是物理连接，也可以是虚连接。在交换系统中完成这一基本功能的部件就是交换网络（Switching Network），或称为互连网络（Interconnection Network），也可称为交换机构（Switching Fabric）。因此交换网络是任何交换系统的核心，连接功能是通信交换系统最基本的功能之一。

不管交换网络内部结构如何，总可以把它看作一个黑箱，对外的特性只有一组入线和一组出线，入线为信息输入端，出线为信息输出端，如图4.14所示。其中，入线可用0～M-1或1～M 的编号来表示，出线可用0～N-1或1～N 的编号来表示。若入线数与出线数相等且均为N，则为N×N 的对称交换网络。

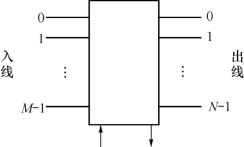
pagenumber_ebook=83,pagenumber_book=70

图4.14　M×N 的交换网络

当有信号到达交换网络的某条入线进行交换时，可以根据出线地址在交换网络内部建立通道，使需交换的信息流从入线沿着已建立的通道流向出线完成交换。通常交换网络内部的通道被称为“连接”，建立内部通道就是建立连接，拆除内部通道就是拆除连接。因此，连接特性是交换网络的基本特性，反映交换网络提供入线到出线的通道的能力。那么，如何描述交换网络的连接特性呢？下面分别从连接集合和连接函数出发来讨论。

1.用连接集合描述交换网络的连接特性

首先，可以把一个交换网络的一组入线和一组出线各看作一个集合，称为入线集合和出线集合，并记为

入线集合：T={0，1，2，…，M-1}

出线集合：R={0，1，2，…，N-1}

定义 t∈T，即t是T 的一个元；r∈Rt，Rt∈R，即Rt是R 的一个子集；r是Rt的一个元，则集合

为一个连接。其中，t为连接的起点，r∈Rt为连接的终点，即交换网络的一个连接就是入线集合T 中的一个元t与出线集合R 中的一个子集Rt组成的集合。

·若r∈Rt，Rt中只含有一个元，则称该连接为一点到另一点（简称点到点）连接；

·若r∈Rt，Rt中含有多个元，则称连接为一点到多点连接。

若一个交换网络可以提供点到多点连接，但Rt≠R，则称其具有同发功能，也可称为多播（Multicast）或组播功能，即从交换网络的一条入线输入的信息可以交换到多条出线上输出；若此时Rt=R，则称该交换网络具有广播（Broadcast）功能，即从交换网络的一条入线输入的信息可以在全部出线上输出。例如，普通的电话通信只需要点到点连接，而像会议电视、有线电视等则需要同发和广播功能。在ATM 交换中，由于点对多点宽带通信业务的需要，多播是一项重要而复杂的功能，不同的ATM 交换系统可采用不同的多播方法。

一个具有一组入线和一组出线的交换网络，上述定义的连接可以同时有多个，这就构成了交换网络的连接集合(https://www.chuimin.cn)

其中，起点集为

TC={t;t∈ci,ci⊂C}

终点集为

RC={r;r∈Rt,Rt⊂ci,ci⊂C}

特别值得注意的是，这里所说的连接和连接集合应该是对应于某一时刻的。一个正在工作的交换网络，某一时刻处于某种连接集合C，不同时刻的连接是可变的，连接集合也是可变的。一个交换网络可能提供的连接集合的数目越多，它的连接能力就越强。

当某一时刻，一个交换网络正处于连接集合C，若一条入线t∈TC，则称该入线t处于占用状态，否则处于空闲状态；同理，若一条出线r∈RC，则称该出线r处于占用状态，否则处于空闲状态。

2.用连接函数描述交换网络的连接特性

下面来讨论用连接函数描述交换网络的连接特性。

每一个交换网络都可用一组连接函数来表示，一个连接函数对应一种连接。连接函数表示相互连接的入线编号和出线编号之间的一一对应关系，即存在连接函数f ，在它的作用下，入线x 与出线f（x）相连接，0≤x≤M-1，0≤f（x）≤N-1。连接函数实际上也反映了入线编号构成的数组和出线编号构成的数组之间对应的置换关系或排列关系。所以连接函数也被称为置换函数或排列函数。另外，从集合角度来讲，一个连接函数反映了入线集合和出线集合的一种映射关系。

用x 表示入线编号变量，用f（x）表示连接函数。通常x 用若干位二进制形式来表示，写成xn-1xn-2…x1x0，如x=6可表示为x2x1x0=110，则连接函数对应地表示为f（xn-1xn-2…x1x0）。例如，某一连接函数表示为

则δ（000）=000，δ（001）=010，δ（010）=100，…，δ（111）=111；即入线0与出线0相连接，入线1与出线2相连接，入线2与出线4相连接……如图4.15所示。

pagenumber_ebook=84,pagenumber_book=71

图4.15　连接函数δ（x2x1x0）=x1x0x2的图形表示

连接功能的数学描述：深入探讨

相关推荐