总体变形分析按隧道的初期支护变形分级标准与可接受准则对兰渝线变形达到Ⅰ级的隧道进行分类梳理。统计分析表明,当最大主应力与隧道轴线呈大夹角时,大变形出现的频率为100%。统计分析表明,软岩大变形发生频率为64.3%,软岩夹中硬岩为30.3%,因此岩层强度是产生大变形的主要因素。兰渝线大变形隧道的统计结果表明,薄层岩体大变形出现频率为82.1%,中厚层为17.9%,厚层及以上一般不会出现大变形。表3.4各因素对围岩变形的影响程度统计分析续表......
2023-09-21
1.剪切的概念和实用计算
(1)剪切的概念与实例
工程上一些连接构件,如常用的销(见图3-39)、螺栓(见图3-40)、平键等都是主要发生剪切变形的构件,称为剪切构件。这类构件的受力和变形情况,可概括为如图3-41 所示的简图,其受力特点是:作用于构件两侧面上横向外力的合力,大小相等、方向相反,作用线相距很近。在这样外力的作用下,其变形特点是:两力间的横截面发生相对错动。这种变形形式称为剪切,发生相对错动的截面称为剪切面。

图3-39 销钉连接
(a)销钉连接工作简图;(b)销钉的受力情况;(c)销钉截面的剪力
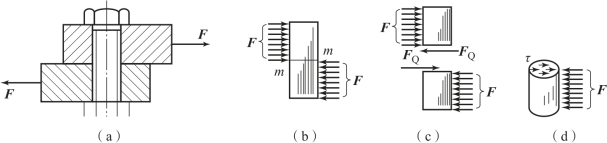
图3-40 螺栓连接
(a)螺栓连接工作简图;(b)螺栓的受力情况;(c)螺栓截面的剪力;(d)螺栓截面的应力
(2)剪切的实用计算
为了对构件进行剪切强度计算,必须先计算剪切面上的内力。现以图3-40(a)所示的螺栓为例进行分析。当两块钢板受拉时,螺栓的受力如图3-40(b)所示。若力F 过大,螺栓可能沿剪切面m-m 被剪断。为了求得剪切面上的内力,运用截面法将螺栓沿剪切面假想截开,如图3-40(c)所示,并取其中一部分研究。由于任一部分均保持平衡,故在剪切面内必然有与外力F 大小相等、方向相反的内力存在,这个内力称为剪力,它是剪切面上分布内力的合力。由平衡方程式ΣF=0,得FQ=F。
剪力在剪切面上分布的情况是比较复杂的,工程上通常采用以实验、经验为基础的实用计算法。在实用计算中,假定剪力在剪切面上均匀分布。前面轴向拉伸和压缩一节中,曾用正应力σ 表示单位面积上垂直于截面的内力;同样,对剪切构件,也可以用单位面积上平行截面的内力来衡量内力的聚集程度,称为切应力,以 表示,其单位与正应力一样。按假定算出的平均切应力称为名义切应力,一般简称为切应力,切应力在剪切面上的分布如图3-40(d)所示。所以剪切构件的切应力可按下式计算,即
表示,其单位与正应力一样。按假定算出的平均切应力称为名义切应力,一般简称为切应力,切应力在剪切面上的分布如图3-40(d)所示。所以剪切构件的切应力可按下式计算,即
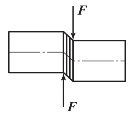
图3-41 剪切变形示意图
![]()
式中,A 为剪切面面积(m2),FQ 为剪切面剪力(N)。
为了保证螺栓安全可靠工作,要求其工作时的切应力不得超过某一许用值。因此螺栓的剪切强度条件为
![]()
式中,[ ]为材料许用切应力(Pa)。
]为材料许用切应力(Pa)。
式(3-23)虽然是以螺栓为例得出的,但也适用于其他剪切构件。
试验表明,一般情况下,材料的许用切应力[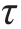 ]和许用拉应力[σ]有以下关系:
]和许用拉应力[σ]有以下关系:
塑性材料:[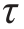 ]=(0.6~0.8)[σ];
]=(0.6~0.8)[σ];
脆性材料:[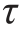 ]=(0.8~1.0)[σ]。
]=(0.8~1.0)[σ]。
运用强度条件,可以进行强度校核、设计截面面积和确定许可载荷等3 种强度问题的计算。
2.挤压的概念和实用计算
(1)挤压的概念与实例
构件在受到剪切作用的同时,往往还伴随着挤压作用。例如,图3-40(a)中的下层钢板,由于与螺栓圆柱面的相互压紧,在接触面上产生较大的压力,致使接触处的局部区域产生塑性变形,如图3-42 所示,这种现象称为挤压。此外,连接件的接触表面上也有类似现象。可见,连接件除了可能以剪切的形式遭到破坏外,也可能因挤压而被破坏。工程机械上常用的平键,经常发生挤压破坏。构件上产生挤压变形的接触面称为挤压面,挤压面上的压力称为挤压力,用Fj 表示。一般情况下,挤压面垂直于挤压力的作用线。
(2)挤压的实用计算
由挤压而引起的应力称为挤压应力,用σj 表示。挤压应力与直杆压缩中的压应力不同,压应力遍及整个受压杆件的内部,在横截面上是均匀分布的,而挤压应力则只限于接触面附近的区域,在接触面上的分布也比较复杂。像剪切的实用计算一样,挤压在工程上也采用实用计算方法,即假定在挤压面上应力是均匀分布的,如果以Fj 表示挤压面上的作用力,Aj 表示挤压面面积,则
![]()
于是,建立挤压强度条件为
![]()
式中,[σj]为材料的许用挤压应力,其数值由试验确定,可从有关设计手册中查到,一般可取:
塑性材料:[σj]=(1.5~2.5)[σ];
脆性材料:[σj]=(0.9~1.5)[σ]。
关于挤压面面积Aj 的计算,要根据接触面的具体情况而定。对于螺栓、铆钉等连接件,挤压时接触面为半圆柱面,如图3-43(a)所示。但在计算挤压应力时,挤压面积采用实际接触面在垂直于挤压力方向的平面上的投影面积,如图3-43(c)所示的ABCD 面积。这是因为从理论分析得知,在半圆柱挤压面上,挤压应力分布如图3-43(b)所示,最大挤压应力在半圆柱圆弧的中点处,其值与按正投影面积计算结果相近。对于键连接,其接触面是平面,故挤压面的计算面积就是接触面的面积。

图3-42 挤压变形
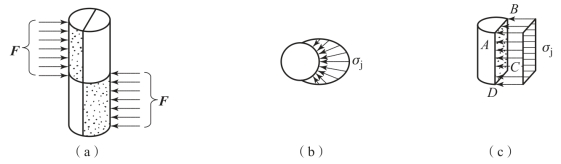
图3-43 圆柱零件挤压图面积的确定
(a)半圆柱面受挤压力作用;(b)圆柱面挤压应力的分布;(c)圆柱零件的挤压面积
【例3-12】 铸铁带轮用平键与轴连接,如图3-44(a)所示。传递的力偶矩T=350 N·m,轴的直径d=40 mm,平键尺寸b×h=12 mm×8 mm,初步确定键长l=35 mm,键的材料为45 钢,许用切应力 [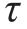 ]=60 MPa,许用挤压应力 [σj]=100 MPa。铸铁的许用挤压应力[σj]=80 MPa。试校核键连接的强度。
]=60 MPa,许用挤压应力 [σj]=100 MPa。铸铁的许用挤压应力[σj]=80 MPa。试校核键连接的强度。
解:以轴(包括平键)为研究对象,其受力图如图3-44(b)所示,根据平衡条件可得

1)校核键的剪切强度。平键的受力情况如图3-44(c)所示,此时剪切面上的剪力为
![]()
![]()
剪切面面积为
所以,平键的工作切应力为
![]()
满足剪切强度条件。
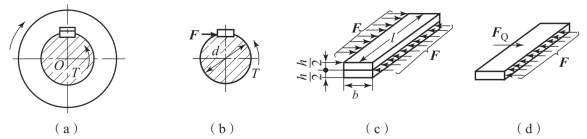
图3-44 平键的受力分析
2)校核挤压强度。由于铸铁的许用挤压应力小,所以取铸铁的许用挤压应力作为核算的依据。
带轮挤压面上的挤压力为
![]()
带轮的挤压面面积与键的挤压面面积相同,设带轮与键的接触高度为h/2,则挤压面面积为
![]()
故带轮的挤压应力为
![]()
不满足挤压强度条件。现需根据挤压强度条件重新确定键的长度。根据式(3-25)有
![]()
即hl/2≥Fj/ [σj],得键的长度
![]()
最后确定键的长度为55 mm。
有关机械基础的文章

总体变形分析按隧道的初期支护变形分级标准与可接受准则对兰渝线变形达到Ⅰ级的隧道进行分类梳理。统计分析表明,当最大主应力与隧道轴线呈大夹角时,大变形出现的频率为100%。统计分析表明,软岩大变形发生频率为64.3%,软岩夹中硬岩为30.3%,因此岩层强度是产生大变形的主要因素。兰渝线大变形隧道的统计结果表明,薄层岩体大变形出现频率为82.1%,中厚层为17.9%,厚层及以上一般不会出现大变形。表3.4各因素对围岩变形的影响程度统计分析续表......
2023-09-21

它对切削力、切削热和积屑瘤的形成与消失及刀具的磨损有着直接的影响。切削脆性材料时,被切层一般经过弹性变形、挤裂和切离三个阶段形成切屑。图3-3切削塑性金属材料的四个阶段弹性变形;塑性变形(滑移);挤裂;切离图3-4切削脆性金属材料的三个阶段弹性变形;挤裂;切离在切削过程中,由于工件材料的塑性和塑性变形(滑移)的程度不同,将会产生不同形状的切屑,见表3-1。......
2023-07-01

为控制围岩变形,保证支护的稳定,项目研究团队研究提出了适合大跨段的多重锁固支护施工技术。1)技术特点强挤压围岩隧道多重锁固支护施工的技术关键点为:排架式结构技术、压浆剂快速锚固锚索技术、锚索预留低预应力柔性张拉技术、三层支护技术。图6.10大跨多重锁固支护示意图图6.11排架式结构支护示意图具体实施步骤如下:①先进行多台阶分部开挖。......
2023-09-21

表1.1列出了国内外典型的挤压性围岩隧道。由此可见,高地应力软岩地质环境引起的挤压大变形破坏是一种严重的工程地质灾害。目前,对围岩挤压性大变形问题的研究,主要依靠归纳、总结及工程类比等方法,其中的主要问题集中在软岩的定义和分类、大变形的定义、机制和分级等几个方面。何满潮等将围岩大变形的判据分为定性方法和定量方法,并给出了日本学者对日本国内挤压性围岩特点及大变形判别研究方面的统计性结果。......
2023-09-21

1)技术特点新城子隧道双联拱段中隔墙厚度太薄,为确保中隔墙的稳定性,采用“背靠背”施工方法。图6.31“背靠背”施工正洞支护①先行右线施工,开挖采用三台阶机械开挖法,开挖完成后及时进行初期支护,采用电镐,将中隔墙一侧提前预埋的中下台阶接头凿出。图6.34位“背靠背”中下台阶钢拱架预埋施工照片。图6.32对拉锚杆与钢架连接示意图图6.33牛腿处的钢架连接示意图图6.34“背靠背”中下台阶钢拱架预埋施工......
2023-09-21

Maya中把关节简化成关节球,通过关节球的旋转使模型发生变形。两个关节之间的部分称为骨骼。Maya中,权重是指变形器、约束对被控制物体影响强度的数值。模块设置图7.6图7.7 IK控制可直接在骨骼末端捕捉到点的位置。Maya的工作原理是把数据及其操作封装为节点,通过这些节点链接,实现数据的流入流出,最终得到计算结果。Maya就是通过节点这种信息流进行运算、管理的。......
2023-11-21

薄层炭质板岩层厚1~5 cm,软弱破碎,无法钻芯取样,只能通过岩体原位测试来研究岩体的力学特性与变形特性。图2.22岩体抗剪试验图2.23岩体抗剪试验-ε曲线从图2.23来看,5个试件的-ε曲线基本呈抛物线形,说明岩体的抗剪断破坏形式基本以塑性破坏为主。表2.6是围岩体抗剪(断)试验正应力与剪应力的关系表,表2.7是围岩体抗剪(断)强度试验的成果汇总表。......
2023-09-21

隧道开挖后出现严重的大变形,变形速率快,变形量大。监测资料显示围岩随着变形持续时间加长,表现出明显的流变效应。支护参数与开挖工法经过多次调整,效果有限,仍无法全面控制围岩变形。②考虑围岩的蠕变特性,视围岩为黏弹塑性体,研究围岩位移、应力及塑性区随时间的变化规律。计算过程中通过布设测点监测位移及应力场随时间发展的变化规律。岩体力学参数采用现场原位测试的结果,蠕变参数采用第4章反演分析得到的结果。......
2023-09-21
相关推荐