把单位面积上内力的大小称为应力,并以此作为衡量受力程度的尺度。截面上的应力可以进行分解,其中垂直于截面的应力为正应力,用字母σ 表示;平行于截面的应力称为切应力,用字母τ 表示。图4-12截面上的应力横截面正应力在国际单位制中,应力的单位是牛/米2,又称帕斯卡,简称帕。为此对杆进行拉伸或压缩实验,观察其变形。求此时斜杆AB 横截面上的正应力。......
2023-06-19
1.杆件轴向拉伸与压缩的概念
在工程实际中,许多构件承受拉力和压力的作用。图3-30 所示为一简易吊车,忽略自重,AB,BC 两杆均为二力杆;BC 杆在通过轴线的拉力的作用下,沿杆轴线发生拉伸变形;而AB 杆则在通过轴线的压力的作用下,沿杆轴线发生压缩变形。再如液压传动中的活塞杆,在油压和工作阻力的作用下受拉,如图3-31 所示。此外,拉床的拉刀在拉削工件时,都承受拉伸;千斤顶的螺杆在顶重物时,则承受压缩。
这些受拉或受压的杆件的结构形式虽各有差异,加载方式也并不相同,但若把杆件形状和受力情况进行简化,都可以画成图3-32 所示的计算简图。这类杆件的受力特点是:杆件承受外力的作用线与杆件轴线重合;变形特点是:杆件沿轴线方向伸长或缩短。这种变形形式称为轴向拉伸或压缩。
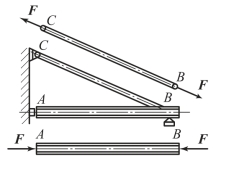
图3-30 简易吊车
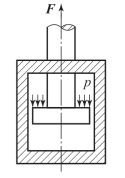
图3-31 液压传动中的活塞
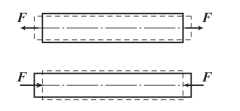
图3-32 拉、压杆力学简图
2.杆件轴向拉伸与压缩的内力和应力
(1)内力
构件工作时承受的载荷、自重和约束力,都称为构件上的外力。构件在外力作用下产生变形,即构件内部材料微粒之间的相对位置发生了改变,则它们相互之间的作用力发生了改变。这种由外力作用而引起的构件内部的相互作用力,称为内力。
构件横截面上的内力随外力和变形的增加而增大,但内力的增大是有限度的,若超过某一限度,构件就不能正常工作,甚至被破坏。为了保证构件在外力作用下安全、可靠工作,必须弄清内力的分布规律,因此对各种基本变形的研究都是首先从内力分析着手的。
(2)截面法
将杆件假想地切开以显示内力,并由平衡条件建立内力与外力的关系或由外力确定内力的方法,称为截面法,它是分析杆件内力的一般方法。其过程可归纳为4 个步骤:
1)截在需求内力的截面处,假想地将杆件截成两部分。
2)任取一段(一般取受力情况较简单的部分)为研究对象。
3)在截面上用内力代替截掉部分对该段的作用。
4)对所研究的部分建立平衡方程,求出截面上的未知内力。
(3)轴力与轴力图
1)轴与轴力图的概念。
如图3-33(a)所示,两端受轴向拉力F 的杆件,为了求任一横截面1-1 上的内力,可采用截面法,即假想用与杆件轴线垂直的平面在1-1 截面处将杆件截开;取左段为研究对象,用分布内力的合力FN 来替代右段对左段的作用,如图3-33(b)所示,建立平衡方程,可得
![]()
若取杆件右端来研究,如图3-33(c)所示,则其结果相同。
由于外力F 的作用线沿着杆的轴线,内力FN 的作用线也通过杆的轴线,故在轴向拉伸或压缩时,杆件的内力称为轴力。显然,轴力可以是拉力,也可以是压力。为了便于区别,规定拉力以正号表示,压力以负号表示。
实际问题中,杆件所受外力可能很复杂,这时直杆各横截面上的轴力将不相同,如FN 将是横截面位置坐标x 的函数,即
![]()
用平行于杆件轴线的x 坐标表示各横截面的位置,以垂直于杆轴线的FN 坐标表示对应横截面上的轴力,这样画出的函数图形称为轴力图。
【例3-9】 等截面直杆AD 受力如图3-34(a)所示。已知F1=16 kN,F2=10 kN,F3=20 kN,试画出直杆AD 的轴力图。
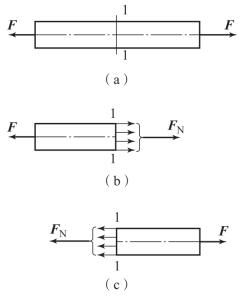
图3-33 截面法求轴力
(a)拉伸杆件;(b)左段分析;(c)右段分析
解:1)计算支反力。
设杆的支反力为FD,由整体受力图建立平衡方程得
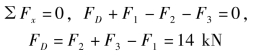
画出直杆AD 的受力图,如图3-34(b)所示。
2)分段计算轴力。
由于在横截面B 和C 处作用有外力,故应将杆分为AB、BC 和CD 3 段,逐段计算轴力。利用截面法,在AB 段的任一截面1-1 处将杆截开,并选择右段为研究对象,其受力情况如图3-34(c)所示。由平衡方程
![]()
得AB 段的轴力为
![]()
对于BC 段,仍用截面法,在任一截面2-2处将杆截开,并选择右段研究其平衡,如图3-34(d)所示,BC 段的轴力为
![]()
为了计算BC 段的轴力,同样也可选择截开后的左段为研究对象,如图3-34(e)所示,由该段的平衡条件得
![]()
对于CD 段,在任一截面3-3 处将杆截开,显然取左段为研究对象计算较简单,如图3-34(f)所示。由该段的平衡条件得
![]()
所得FN3为负值,说明FN3 的实际方向与所假设的方向相反,即应为压力。
3)画轴力图。根据所求得的轴力值画出轴力图,如图3-34(g)所示。由轴力图可以看出,轴力的最大值为16 kN,发生在AB 段内。
(3)轴力图的快速画法
轴力图也可根据轴力、轴力图随外力的变化规律快速作图。
1)轴力、轴力图随外力的变化规律。
①在没有外力作用处,轴力是常数,轴力图是水平线。
②在有外力作用处,轴力图有突变,突变量等于外力。
2)轴力图的画法。
①先求出约束反力,约束反力与外力同等看待,画出杆件的受力图,如图3-34(b)所示。
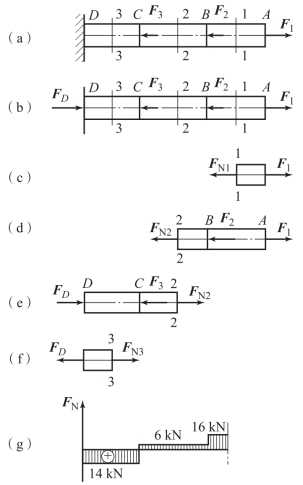
图3-34 杆的轴力分析
②以构件左端为原点,x 轴表示为构件轴线,垂直于杆轴线的表示轴力FN。
③假设向左的外力产生正的轴力(轴力图在该处垂直向上突变,突变量等于外力),向右的外力产生负的轴力(轴力图在该处垂直向下突变,突变量等于外力)。
④根据轴力、轴力图的变化规律画出轴力图,如图3-34(g)所示。
(4)杆件拉(压)杆横截面上的应力
1)应力的概念。确定了轴力后,单凭轴力并不能判断杆件的强度是否足够。杆件的强度不仅与轴力的大小有关,而且还与横截面积的大小有关,即取决于内力在横截面上分布的密集程度。内力在横截面上的密集度称为应力。如果内力在截面上均匀分布,则应力就是单位面积上的内力。其中,垂直于截面的应力称为正应力,以σ 表示;平行于截面的应力称为切应力(剪应力),以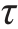 表示。应力的单位为帕斯卡,符号为Pa(1 Pa=1 N/m2),由于此单位较小,故常采用兆帕(MPa)或吉帕(GPa)(1 MPa=106 Pa,1 GPa=109 Pa)。
表示。应力的单位为帕斯卡,符号为Pa(1 Pa=1 N/m2),由于此单位较小,故常采用兆帕(MPa)或吉帕(GPa)(1 MPa=106 Pa,1 GPa=109 Pa)。
2)拉(压)杆横截面上的应力。为了求得横截面上任意一点的应力,必须了解内力在横截面上的分布规律,为此可通过实验来分析研究。取一等直杆,在杆上画上与杆轴线平行的纵向线和与它垂直的横线,如图3-35(a)所示。
在两端施加一对轴向拉力F 之后,可以发现所有纵向线的伸长都相等,而横向线仍保持为直线,并与纵向线垂直,如图3-35(b)所示。据此现象可设想,杆件由无数纵向纤维所组成,且每根纵向纤维都受到同样的拉伸。假设在变形过程中,横截面始终保持为平面(即平面假设),根据材料的均匀连续性假设可推知,横截面上各点处纵向纤维的变形相同,受力也相同,即内力在横截面上是均匀分布的,且与横截面垂直,如图3-35(c)所示。

图3-35 拉伸应力
设杆件横截面的面积为A,轴力为FN,则根据上述假设可知,横截面上各点处的正应力均为
![]()
式中,FN 为横截面的轴力(N);A 为横截面积(mm2)。
3.杆线轴向拉伸和压缩的强度计算
(1)极限应力、许用应力、安全系数
试验表明,塑性材料的应力达到屈服强度σs(σ0.2)后,产生显著的塑性变形,影响构件的正常工作;当脆性材料的应力达到抗拉强度或抗压强度时,发生脆性断裂破坏。构件工作时,发生显著的塑性变形或断裂都是不允许的,通常将发生显著的塑性变形或断裂时的应力称为材料的极限应力,用σu 表示。对于塑性材料,取σu=σs(σu=σ0.2);对于脆性材料,取σu=σb。
考虑到载荷估计的准确程度、应力计算方法的精确程度、材料的均匀程度以及构件的重要性等因素,为了保证构件安全、可靠地工作,应使它的最大工作应力小于材料的极限应力,使构件留有适当的强度储备。一般把极限应力除以安全系数n(n >1)后的值作为设计时应力的最大允许值,称为许用应力,用[σ]表示,即
![]()
正确地选择安全系数关系到构件的安全与经济这一对矛盾的问题,过大的安全系数会浪费材料,过小的安全系数则又可能使构件不能安全工作。各种不同工作条件下构件安全系数n 的选取,可从有关工作手册中查找。一般对于塑性材料,取n=1.3~2.0;对于脆性材料,取n=2.0~3.5。
(2)拉(压)杆的强度条件
为了保证轴向拉(压)杆在载荷作用下安全工作,必须使杆内的最大工作应力σmax不超过材料的许用应力[σ],即
![]()
式中,FNmax和A 分别为危险截面上的轴力及其横截面积。
利用强度条件,可以解决下列3 种强度计算问题:
1)校核强度。已知杆件的尺寸、所受载荷和材料的许用应力,根据强度条件,校核杆件是否满足强度条件。
2)设计截面尺寸。已知杆件所承受的载荷及材料的许用应力,根据强度条件可以确定杆件所需横截面积A。例如,对于等截面拉(压)杆,其所需横截面积为
![]()
3)确定许可载荷。已知杆件的横截面尺寸及材料的许用应力,根据强度条件可以确定杆件所能承受的最大轴力,其值为
![]()
【例3-10】 简易悬臂吊车如图3-36 所示,AB 为圆截面钢杆,横截面积A1=600 mm2,许用拉应力[σ+]=160 MPa;BC 为圆截面木杆,横截面积A2=10 ×103 mm2,许用压应力为[σ-]=7 MPa。若起吊量FG=45 kN,问此结构是否安全?最大起吊量是多少?
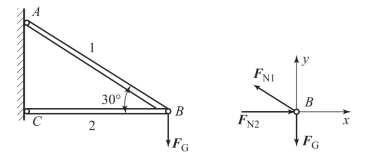
图3-36 悬臂吊车
解:1)求两杆的轴力。分析节点B 的平衡,有
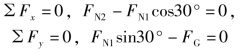
由上式可解得

2)校核强度。根据轴向拉(压)强度条件,AB、BC 杆的最大应力为
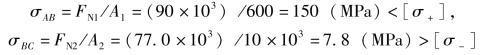
可见,BC 杆的最大工作应力超过了材料的许用应力,所以此结构不安全。
由上面计算可知,若起吊量FG=45 kN,则此结构危险,那么现在要问最大起吊量为多少? 这就需要确定许可载荷。
根据钢杆AB 的强度要求,有
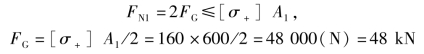
根据木杆BC 的强度要求,有
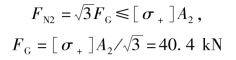
可见,吊车的最大起吊量,即许用载荷为FG=40.4 kN。
4.胡克定律、轴向拉伸和压缩的变形计算
(1)纵向线应变和横向线应变
杆件在轴向拉伸或压缩时,沿轴线方向伸长或缩短,与此同时,横向尺寸还会缩小或增大。前者称为纵向变形,后者称为横向变形。如图3-37 所示,设杆原长为l,横向尺寸为d,承受轴向拉力F,变形后的长度为l1,横向尺寸为d1,则杆的纵向绝对变形为
![]()
杆的横向绝对变形为
![]()
为了消除杆件原尺寸对变形大小的影响,用单位长度内杆的变形,即线应变来衡量杆件的变形程度。与上述两种绝对变形相对应的纵向线应变为
![]()
横向线应变为
![]()
(2)轴纵向变形的规律
轴向拉伸和压缩时,应力和应变之间存在着一定的关系,这一关系可通过试验测定。试验表明,当杆内的轴力FN 不超过某一限度时,杆的绝对变形Δl 与轴力FN 及杆长l 成正比,与杆的横截面积A 成反比,即
![]()
式(3-20)所表示的关系,称为胡克定律。式(3-20)中,E 称为弹性模量,其值随材料而异,可由试验测定,单位为GPa。材料的E 值越大,应变就越小,故它是衡量材料抵抗弹性变形能力的一个指标。
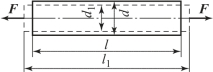
图3-37 拉杆的变形
利用ε=Δl/l 和σ=FN/A,式(3-20)可改写为
![]()
式(3-21)为胡克定律的另一表达形式。
【例3-11】 图3-38(a)所示为阶梯杆。已知横截面积AAB=ABC=500 mm2,ACD=300 mm2,弹性模量E=200 GPa,试求整个杆的变形量。
解:1)作轴力图。求出约束反力,FNA=-20 kN,画出杆AB 的受力图,如图3-38(b)所示。
2)用轴力图的快速画法画出杆AB 的轴力图,如图3-38(c)所示。
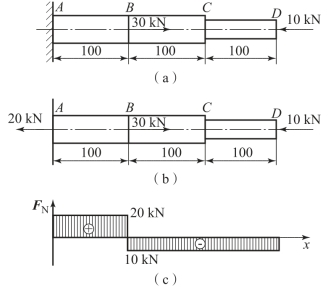
图3-38 阶梯直杆
3)计算各段杆的变形量,则
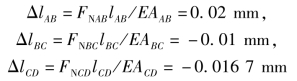
4)计算杆的总变形量。杆的总变形量等于各段变形量之和,即
![]()
计算结果为负,说明杆的总变形为压缩变形。
有关机械基础的文章

把单位面积上内力的大小称为应力,并以此作为衡量受力程度的尺度。截面上的应力可以进行分解,其中垂直于截面的应力为正应力,用字母σ 表示;平行于截面的应力称为切应力,用字母τ 表示。图4-12截面上的应力横截面正应力在国际单位制中,应力的单位是牛/米2,又称帕斯卡,简称帕。为此对杆进行拉伸或压缩实验,观察其变形。求此时斜杆AB 横截面上的正应力。......
2023-06-19

图4-9截面的内力3.轴力与轴力图轴力的概念。为保证无论取左段还是右段作研究对象所求得的同一个横截面上轴力的正负号相同,对轴力的正负号规定如下:轴力的方向与所在横截面的外法线方向一致时,轴力为正;反之为负。用截面法在AB、BC 两段,逐次计算轴力。图4-11直杆的轴力与轴力图......
2023-06-19

如果杆件除了在通过其轴线的纵向平面内受到垂直于轴线的荷载以外,还受到轴向拉(压)力,这时杆将发生拉伸(压缩)和弯曲组合变形。例如,如图8-3所示的烟囱,在自重作用下引起轴向压缩,在风力作用下引起弯曲,因此它是轴向压缩与弯曲的组合变形。这里首先推导(公论)扭弯组合变形的强度计算方法,计算原理和拉伸或压缩与弯曲的组合变形基本相似,本章就不作介绍。......
2023-06-16

如图2.1所示的结构上作用荷载F,AB杆为钢杆,其横截面直径d=20mm;BC杆为木杆,其横截面为边长a=100mm的正方形。由于AB杆和BC杆的材料不同,其许用应力也不相同,故需要分别校核其强度。图2.1例题2.1图图2.2计算各杆轴力。取结点B进行分析,建立坐标系,其受力图如图2.2所示。如图2.3所示,AB是刚性杆,在B端受力偶Me作用,已知CD杆的截面积A=500mm2,E=200GPa,[σ]=160MPa,l=1m。图2.3例题2.2图图2.4确定最大荷载Me。CD杆的变形考虑变形后的几何关系,可知......
2023-06-20

反之,在轴向压力作用下,将引起轴向的缩短和横向的增大。因此,必须研究杆件的变形。与上述两种绝对变形相对应的纵向线应变为横向线应变线应变表示的是杆件的相对变形。即式(4-5)称为虎克定律。常数E 称为材料的弹性模量,其值随材料而异,可由试验测定。试求整个杆的变形量。......
2023-06-19

图0-5图0-6等截面杆;变截面杆2.杆件变形的基本形式杆件受外力作用后,其几何形状和尺寸一般都要发生改变,这种改变量称为变形。杆件在不同形式的外力作用下,将发生不同形式的变形。总的来说,杆件变形的基本形式有以下四种:轴向拉伸或压缩[图0-7、]。图0-8所示为微小正六面体。上述微小正六面体的各边缩小为无穷小时,通常称为单元体。......
2023-08-26

8-1 如图8-15 所示,各杆的AB、BC、CD(或BD)各段横截面上有哪些内力?图8-16题8-2图8-3 如图8-17 所示,斜梁AB 的横截面为正方形,边长为a=100 mm,F=3 kN,试计算其横截面上最大的拉应力和最大的压应力。图8-17题8-3图8-4 开口链环由直径d=12 mm 的圆钢弯制而成,其形状如图8-18 所示。图8-19题8-5图图8-20题8-6图8-7 如图8-21 所示的支架,已知载荷F=45 kN,作用在C 处,支架材料的许用应力[σ]=160 MPa,试选择横梁AC 的工字钢型号。......
2023-06-19

由式(5-1)可知,拉(压)杆的工作应力,为了保证构件能安全正常地工作,则杆内最大的工作应力不得超过材料的许用应力。即式(5-8)称为拉(压)杆的强度条件。在轴向拉(压)杆中,产生最大正应力的截面称为危险截面。应用强度条件式(5-8)可以解决轴向拉(压)杆强度计算的三类问题。如,表示杆件的强度是满足要求的,否则不满足强度条件。......
2023-06-16
相关推荐