于是可得到平面一般力系的合力矩定理。平面一般力系的合力对作用面内任一点的矩等于力系中各力对同一点的矩的代数和。因此，在平面力系情况下，固定端支座的约束反力包括三个：即阻止梁端向任何方向移动的水平反力XA和竖向反力YA，以及阻止物体转动的反力偶MA。试将这三个力向底面中心O点简化，并求简化的最后结果。......
2025-09-29
力矩和平面力偶系的分析方法
【摘要】：力偶两力之间的垂直距离d 称为力偶臂，力偶所在的平面称为力偶的作用面。力偶矩的单位与力矩的单位相同。用M 表示合力偶矩，则合力偶矩的代数式为当平面力偶系的合力偶矩等于零时，力偶系对物体的转动效应为零，物体处于平衡状态。因4 个螺栓受力均匀，即F1＝F2＝F3＝F4＝F，此4 个力组成两个力偶。
1.平面力对点之矩
（1）力矩
在日常生活和工程建设中，我们常用扳手来拧紧螺母，如图3－21 所示。由经验可知，拧动螺母的作用力不仅与F 的大小有关，而且与点O 到力的作用线的垂直距离有关。因此力F 对扳手的作用可用两者的乘积Fd来量度。显然，力F 使扳手绕点O 转动的方向不同，作用效果也不同。
图3-21 用扳手拧螺母示意图
由此可见，力F 使物体绕O 转动的效果，完全由下列两个因素决定：
1）力的大小与力臂的乘积Fd。
2）力使物体绕O 点转动的方向。
这两个因素可用一个代数量表示为
这个代数量称为力对点的矩，简称力矩。
力矩的概念可以推广到普遍的情形。在图3－21 中，平面上作用一力F，在平面内任取一点O，点O 称为矩心，点O 到力的作用线的垂直距离d 称为力臂，则在平面问题中力对点的矩的定义如下：
力对点的矩是一个代数量，它的绝对值等于力的大小与力臂的乘积，它的正负可按以下方法来确定：力使物体绕矩心逆时针转向转动时为正，反之为负。
由图3－ 21 可知，力F 对点O 的矩的大小可用△AOB 面积的两倍表示，即
力矩在下列两种情况下等于零：力等于零；力的作用线通过矩心，即力臂等于零。力矩的单位为N·m。
【例3-6】 直杆AB 长0.5 m，A 点受固定铰链约束，B 点受F1，F2，F3，F4 4 个力作用，如图3－22 所示。4 个力的大小分别为F1＝100 N，F2＝50 N，F3＝60 N，F4＝80 N。试求各力对A 点的力矩。
解：各力对A 点的力矩为
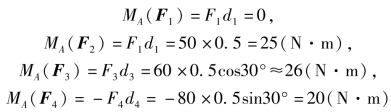
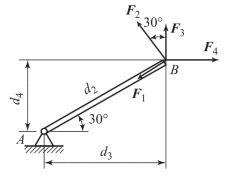
图3-22 直杆的力矩
（2）合力矩定理
根据合力的定义，合力对物体的作用效果等于力系中各分力对物体作用效果的总和。既然力对物体的转动效应是用力矩来度量的，那么合力对某点的力矩等于各分力对该点力矩的代数和。这个关系就称为合力矩定理。合力矩定理的数学表达式为
式中，R 为力系F1，F2…，Fn 的合力。
【例3-7】 曲杆AB 一端固定，另一端受力T 的作用，如图3－23（a）所示。若T＝500 N，求T 对A 点的力矩。
解：先将T 分解为互相垂直的两个分力T1，T2，如图3－23（b）所示。根据合力矩定理，有
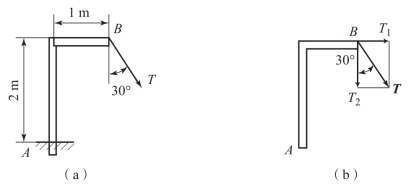
图3-23 曲杆的力矩
2.力偶及力偶矩
（1）力偶
在现实生活或工程实际中，我们常常见到汽车驾驶员用双手转动转向盘驾驶汽车，如图3－24（a）所示；钳工用丝锥攻螺纹，如图3－24（b）所示；电动机的定子磁场对转子的作用，如图3－24（c）所示。在转向盘、丝锥、转子等物体上，作用了一对等值、反向的平行力。等值反向平行力的合力显然等于零，但是由于它们不共线而不能相互平衡，故会使物体改变转动状态。这种由两个大小相等、方向相反的平行力组成的力系，称为力偶，记作（F，F′）。力偶两力之间的垂直距离d 称为力偶臂，力偶所在的平面称为力偶的作用面。既然力偶不能合成为一个力，或用一个力来等效替换，那么力偶也不能用一个力来平衡。因此，力和力偶是静力学的两个基本要素。
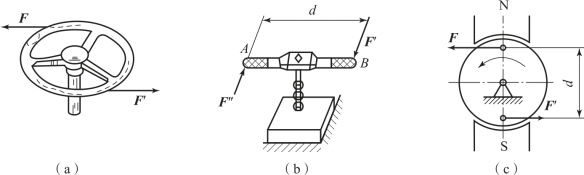
图3-24 力偶作用实例(https://www.chuimin.cn)
（2）力偶矩
力偶对受力物体有转动效应，其大小可用力偶矩来度量。力偶对转动中心的力矩称为力偶矩，用字母m 表示。假定组成力偶的两个力为F 和F′，其间距为d，逆时针转向，如图3－25 所示。这时，力偶矩的大小应为力偶中两力F、F′分别对转动中心O 点力矩的代数和，即图3－25中力偶矩的计算
因为力F 与F′大小相等，故上式变为m＝Fd。
由此可知，力偶对矩心的矩仅与力F 和力偶臂d 的大小有关，而与矩心位置无关，即力偶对物体的转动效应仅取决于力偶中力的大小和两力之间的垂直距离（力偶臂）。因此，通常用乘积Fd，并冠以适当的正负号来度量力偶对物体的转动效应，以m 表示，称为力偶矩，即
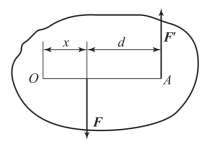
图3-25 力偶矩的计算
它是一个代数量，其正、负号的规定是：当力偶逆时针方向转动时为正，顺时针方向转动时为负。力偶矩的单位与力矩的单位相同。
（3）力偶的三要素
力偶对物体产生的转动效应取决于力偶矩的大小、力偶在其作用面内的转向和力偶的作用面这3 个要素，力学中把这3 个要素称为力偶的三要素。所以，在描述一个力偶时，可以只说明其力偶矩的大小、转向和作用面，如图3－26 所示。
（4）力偶的性质
1）力偶没有合力。因力偶中的两个力等值、反向、平行但不共线，所以这两个力在任一轴上投影的代数和均等于零，如图3－27 所示。
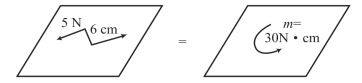
图3-26 力偶的表示
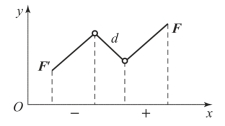
图3-27 力偶在轴上投影示意图
2）力偶不能与一个力等效，而只能与另一个力偶等效。同一平面的两个力偶，只要它们的力偶矩大小相等、转动方向相同，则两力偶必等效。
3）力偶的可移性：力偶在其作用面内可任意移动，而不改变它对物体的作用效果。
4）只要力偶矩的大小和转动方向不变，可同时改变力的大小和力偶臂的长短，而不改变力偶对物体的作用效果。
3.平面力偶系的合成与平衡
作用于物体同一平面内的一组力偶称为平面力偶系。可以证明，平面力偶系可以合成为一个合力偶，此合力偶之矩等于原力偶系中各力偶之矩的代数和。用M 表示合力偶矩，则合力偶矩的代数式为
当平面力偶系的合力偶矩等于零时，力偶系对物体的转动效应为零，物体处于平衡状态。因此，平面力偶系平衡的充要条件是力偶系中各力偶矩的代数和等于零，即
【例3-8】 如图3－28 所示，联轴器上有4 个均匀分布在同一圆周上的螺栓A、B、C、D，该圆周的直径AC＝BD＝200 mm。电动机传给联轴器的力偶矩m＝5 kN·m，试求每个螺栓的受力。
解：1）作用在联轴器上的力为电动机施加的力偶，每个螺栓反力的方向如图3－28 所示。因4 个螺栓受力均匀，即F1＝F2＝F3＝F4＝F，此4 个力组成两个力偶（平面力偶系）。
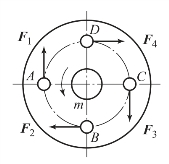
图3-28 联轴器受力分析
2）列平衡方程。联轴器等速转动时，平面力偶系平衡，故
即m－F×AC－F×BD＝0。因为AC＝BD，故
即每个螺栓受力均为12.5 kN，其方向分别与F1、F2、F3、F4 的方向相反。
相关文章
- 详细阅读
-
如何让平面力偶系实现平衡？详细阅读
由合成结果可知，力偶系平衡时，其合力偶的矩等于零。因此，平面力偶系平衡的充分和必要条件是：各力偶矩的代数和等于零，即案例3.9 横梁AB 受到M=-100 N·m 的力偶作用，如图3-25 所示，横梁长度l=5 m，求支座A、B 的反力。梁上有主动力偶的力偶矩M，A、B 处的约束反力FA、FB，根据力偶必须由力偶来平衡的性质，则FA、FB 必组成一力偶。设4 个螺栓的受力均匀，即FA=FB=FC=FD=F，则组成两个力偶并与电动机传给联轴器的力偶平衡。......
2025-09-29
-
平面低副机构：结构和维护详细阅读
平面连杆机构是所有机构全部用低副连接而成的平面机构，又称平面低副机构。因而，平面连杆机构在各种机械和仪器中获得了广泛使用。平面连杆机构中最常见的是由四个构件组成的四杆机构。其中，AD为机架，与机架相连的杆AB、CD称为连架杆。平面连杆机构的结构和维护平面连杆机构是面接触的低副机构，低副中的间隙会引起运动误差，所以要注意保证良好的润滑以减少摩擦、磨损。......
2025-09-29
-
电气总平面图和电气平面图的图线设计与标准详细阅读
电气总平面图和电气平面图宜采用3种及以上线宽绘制，以清楚地表示上述项目之间的关系。建筑电气专业的图线宽度应该根据图线的类型、比例和复杂程度，按现行国家标准《房屋建筑制图统一标准》的规定选用，并宜为0.5、0.7和1.0。表12-1 建筑电气制图图线、线型及线宽当采用b=0.7和0.5的线宽组时，0.25b细线分别为0.18和0.12，图线中的细线可采用0.18和0.13两种线宽，也可统一采用0.13这一种线宽。......
2025-09-29
-
平面铣的类型和子类型介绍详细阅读
在创建平面铣工序时，系统会弹出图3.2.1所示的“创建工序”对话框，在此对话框中显示出了所有平面铣工序的子类型。下面将对其中的子类型作简要介绍。......
2025-09-29
-
如何创建基准曲线和基准平面？详细阅读
Step2.创建图8.8.4所示的基准平面DTM1。单击“创建草绘基准曲线”按钮；选取DTM1基准平面为草绘平面，RIGHT基准平面为草绘平面的参考平面，参考方位是；绘制如图8.8.6所示截面草图。单击工具栏上的“创建基准平面”按钮；选取TOP基准平面为参照平面，偏移值为5.0。按住Ctrl键，选择RIGHT基准平面；单击“基准轴”对话框中的按钮Step7.创建图8.8.11所示的基准平面DTM3。......
2025-09-29
- 详细阅读
- 详细阅读
相关推荐