数学形态学分析在焊接中的应用及其优势

2025-09-29 理论教育版权反馈

【摘要】：由于数学形态学的非线性特点，近年来在抑制噪声、特征提取、边缘检测、图像分割、形状识别、骨架化、纹理分析、颗粒分析、图像增强与恢复、图像压缩等所有图像处理领域都展示了极为美好和广阔的应用前景。

数学形态学（Mathematical Morphology）是研究数字图像形态结构特征与快速并行处理方法的理论，是通过对目标图像的形态变换来实现结构分析和特征提取的目的。数学形态学自2025年由Metheron和Serra提出，而后逐渐发展成为一门较为成熟的数学分支，并逐渐成为图像集合特征分析与处理的有力工具。特别是数学形态学中的基于集合的数学理论，使图像的分析和处理从线性到非线性算法的探讨具备了更加坚实的理论基础。自20世纪90年代中期以来，小波变换、模糊逻辑、多尺度分析等理论先后与数学形态学融合形成非线性分析工具渐成研究热点。

数学形态学摒弃了传统意义上用数值分析和建模来处理图像的观点，是一种基于集合观点的非线性图像处理与分析理论，其运算是在集合基础上定义的，图像全部都以合理的方式转换为集合。因此，数学形态学算子的性能将主要以几何的方式进行刻画，这种显式的几何描述特点更适合视觉信息的处理和分析。数学形态学的基本思想是利用结构元素去探测图像，看它是否能够将这个结构元素很好地填放在图像的内部，同时验证填放结构元素的方法是否有效。由于数学形态学的非线性特点，近年来在抑制噪声、特征提取、边缘检测、图像分割、形状识别、骨架化、纹理分析、颗粒分析、图像增强与恢复、图像压缩等所有图像处理领域都展示了极为美好和广阔的应用前景。数学形态学能将大量的复杂图像处理转换为基本的逻辑和移位运算的组合来完成，其运算速度非常快，用于图像处理效率很高，便于并行处理和硬件实现，非常适于实时过程控制。

数学形态学最早的研究对象就是二值图像，称为二值形态学。二值图像处理中，数学形态学通过结构元素在图像范围内平移，同时施加交、并等基本集合运算来探测和分析所研究的图像。“探针”，即“结构元素”，也是一个集合，它的具体形状依据分析的目的来决定。结构元素可以是线形、三角形、圆形、球形以及由基本的几何结构组合而成的不大于被探测图像的任意形状和尺度的结构。二值图像基本的形态学变换有4种，分别是腐蚀（Erosion）、膨胀（Dilation）、开运算（Open）和闭运算（Close）。

1.二值图像的腐蚀运算

腐蚀是数学形态学的基本运算。它的实现是基于填充结构元素的概念。利用结构元素填充的过程，取决于一个基本的欧氏空间运算——平移。将一个集合A平移距离x可以表示为A+x，其定义为

A+x={a+x：a∈A} （5-3-9）

如图5-3-28所示，从几何上看A+x表示A沿矢量x平移了一段距离。探测的目的就是标记出图像内部那些可以将结构元素填入的平移位置。

集合X被集合S腐蚀，表示为XΘS，其定义为

XΘS={x：S+x⊂X}（5-3-10）其中，⊂表示子集的关系。腐蚀还可以用E（X，S），（X，S）和ERODE（X，S）来表示。其中X为输入图像，S为结构元素。如果结构元素包括原点，则腐蚀具有收缩图像的作用。

对一个给定目标图像X和一个结构元素S，将S在图像上移动。在每一个当前位置x，S[x]只有以下3种可能状态：

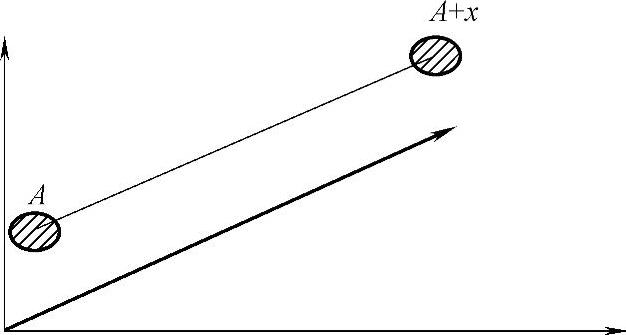
图5-3-28 结构元素平移示意图

1）S[x]⊆X。

2）S[x]⊆X^c。

3）S[x]∩X和S[x]∩X^c均不为空。

第一种情形说明S[x]与X最大相关；第二种情形说明S[x]与X不相关；第三种情形说明S[x]与X只是部分相关。

满足（1）的x的全体构成了结构元素与图像的最大相关点集，这个集合称为S对X的腐蚀，记为XΘS：

XΘS={x|S[x]⊆X}（5-3-11）

腐蚀可以看做是将图像X中每一个与结构元素S全等的子集S[x]收缩为点x，腐蚀在数学形态学运算中的作用是消除物体边缘点。如图5-3-29所示，腐蚀运算的过程：逐步地平移结构元素，且仅当结构元素完全包含于物体内时，当前的平移点才可归入腐蚀后的物体中。

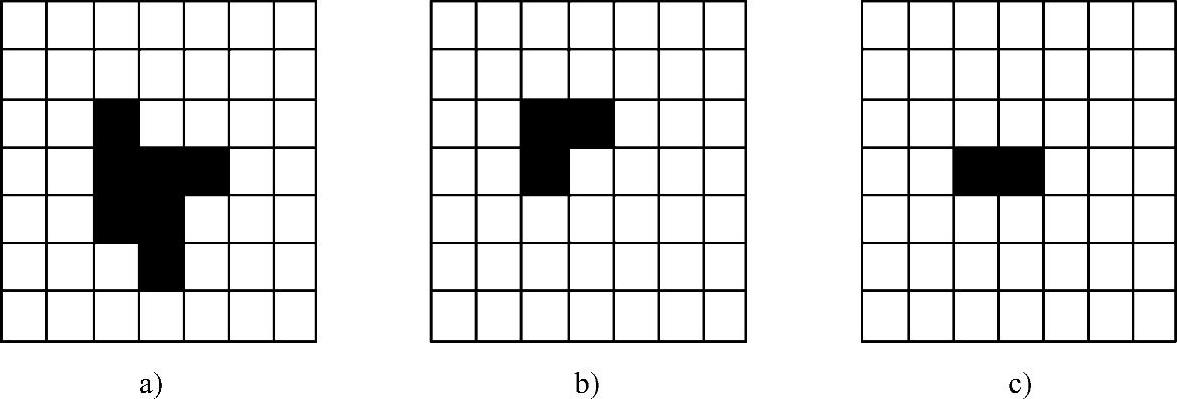
图5-3-29 腐蚀算法示意图

a）原始图像 b）结构元素 c）腐蚀后的图像

2.二值图像的膨胀运算

膨胀是腐蚀的对偶运算，可以通过补集来定义。X被S膨胀可以表示为X⊕S，其定义为

其中，X^c表示X的补集。为了利用S膨胀X，可将S相对原点旋转180°得到-S，在利用-S对X进行腐蚀运算，则腐蚀结果的补集便是所求的结果。膨胀运算具有扩大图像的作用，膨胀可以看做将图像X中的每一个点x扩大为S[x]。

腐蚀运算是将图像X中每一个与结构元素S全等的子集S[x]收缩为点x。反之，也可以将X中的每一个点x扩大为S[x]。这就是膨胀运算，记为X⊕S，其定义为

X⊕S={x|S[x]∩x≠ϕ} （5-3-13）

等价于

X⊕S=∪{X[s]|s∈S} （5-3-14）

X⊕S=∪{S[x]|x⊂X} （5-3-15）

如图5-3-30所示，膨胀运算的过程：将结构元素进行反射，逐步地平移结构元素，如果它与物体相交不为空，则当前的平移点归入形态学腐蚀后的物体。

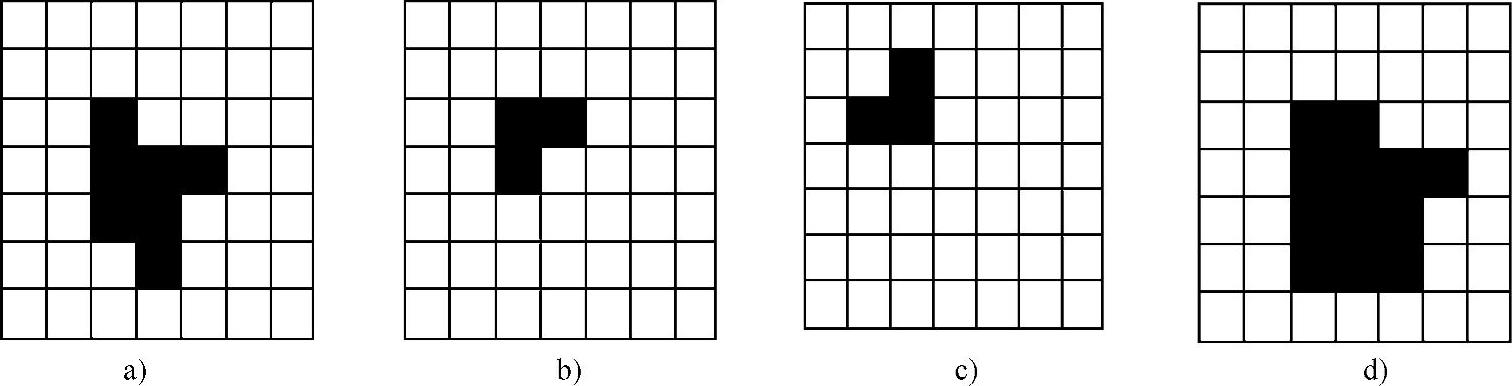
图5-3-30 膨胀算法示意图像

a）原始图像 b）结构元素 c）结构元素反射 d）膨胀后图像(https://www.chuimin.cn)

在形态学中除了腐蚀和膨胀两种基本的运算外，还有两种重要的二次运算，即形态学的开运算和闭运算。虽然开、闭运算是以腐蚀和膨胀定义的，但是，从结构元素的填充角度来看，它具有更为直观的几何形式，这也是二值形态学应用的基础。

3.二值图像的开运算

利用结构元素S对图像X作开运算，其实就是先做腐蚀然后做膨胀，用符号X。S表示，其定义为

X。S=（XΘS）⊕S （5-3-16）

开运算还可以用其他的符号表示，如O（X，S），OPEN（X，S）和X_S。为了更好地理解开运算在图像处理中的作用，有下面的等价公式：

X。S=∪{S+x：S+x⊂X} （5-3-17）

式（5-3-17）表示，开运算可以通过计算所有可以填入图像内部的结构元素平移的并集求得。即对每一个可以填入位置作标记，计算结构元素平移到每一个标记位置的并，便可以得到开运算的结果。事实上，这正是先做腐蚀，然后做膨胀运算的结果。开运算具有磨光图像外边界的作用。先腐蚀后膨胀所描述的开运算如图5-3-31所示。

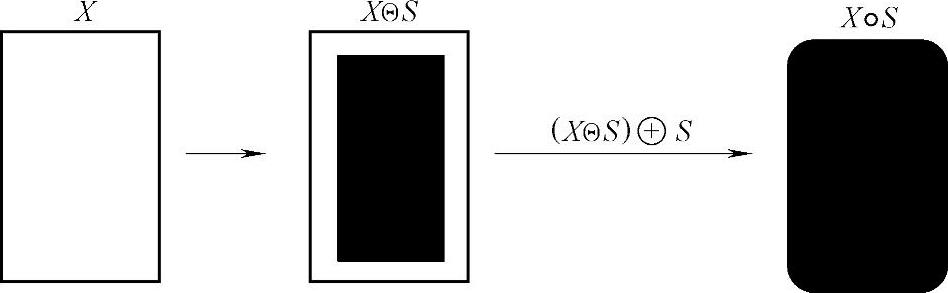
图5-3-31 开运算示意图

4.二值图像的闭运算

闭运算是开运算的对偶运算，定义为先做膨胀然后做腐蚀。闭运算具有磨光图像内边界的作用。利用S对X作闭运算表示为X·S，其定义为

X·S=[X⊕（-S）]Θ（-S）（5-3-18）

闭运算还可以表示为C（X，S），CLOSE（X，S）和X^S。闭运算满足下面的关系：

5.灰度形态学

数学形态学是研究数字图像形态结构特征与快速并行处理方法的理论，是通过对目标图像的形态变换来实现结构分析和特征提取的目的。二值形态学是数学形态学在图形领域最初取得的研究结果，但是在实际应用中，往往会遇到很多灰度图形，直接使用二值形态学的算法显然是不行的。于是人们提出了很多有关灰度形态学的有效算法，使得形态学在图像处理中的应用日益广泛和重要。灰度形态学研究的主要对象是灰度图像，一般用定义在欧氏空间Rn上的一个实值函数f（x）来描述。灰度形态学是二值形态学的自然扩展，但是，对于二值形态学而言，由于它是基于集合运算的，这一表象在灰度形态学中不能直接使用。因此，后人建立的灰度形态学理论必须将函数转化为集合来处理。转化方法一般有两种，即截集（Cross Section）变换和伞顶（Umbrella Top）变换。

建立灰度形态学变换是指将二值形态学中的交、并运算，分别用灰度形态学中最大、最小极值运算来代替，而灰度形态学的腐蚀和膨胀过程则可直接从图像和结构元素的灰度级函数计算出来。

与二值形态学一样，灰度形态学的基本运算也有4个，分别为膨胀运算、腐蚀运算、开运算和闭运算。设f（x）为灰度图像的灰度函数，s（x）为结构元素[其中f（x）∈R，s（x）∈R，x∈Z²]，而D_f和D_s（D_f⊂Rⁿ，D_s⊂Rⁿ）分别为函数f（x）、s（x）的定义域，则f（x）关于s（x）的主要灰度形态学变换定义如下：