分形理论在焊接中的应用探析

2023-06-26 理论教育版权反馈

【摘要】：分形理论的诞生才不过20多年，但它对多种科学产生了巨大的影响。分形理论长期以来一直被认为是对病态的、奇形怪状的、不规则的等一大类自然现象提供一种极其简洁的数学描述方法。目前，分形理论已被广泛应用于自然科学与社会科学的众多领域，在图像处理方面已经被应用于图像边缘检测、图像编码、图像压缩等领域。因此，采用分形这种非线性的图像处理算法对焊接图像进行预处理。

1975年B.B.Mandelbrot在巴黎出版了法文著作《Les obiects fractals：forme，basard et dimen-sion》，标志着分形理论的正式诞生。1977年B.B.Mandelbrot在美国出版了其英文著作《Fractals：Form，Chance，and Dimension》。同年，他又出版了《The fractal Geometry of Nature》。这三本书并没有引起社会上太多人的关注，直到1982年，随着《The fractal Geometry of Nature》第二版的问世，在美国乃至欧洲，迅速形成了“分形热”。分形理论的诞生才不过20多年，但它对多种科学产生了巨大的影响。

分形理论长期以来一直被认为是对病态的、奇形怪状的、不规则的等一大类自然现象提供一种极其简洁的数学描述方法。分形理论作为近十几年来发展起来的一门新的数学理论，其研究对象是不规则但又具有统计自相似性的图形。目前，分形理论已被广泛应用于自然科学与社会科学的众多领域，在图像处理方面已经被应用于图像边缘检测、图像编码、图像压缩等领域。

焊接图像处理的关键是滤波和边缘检测，常用的图像处理算法如微分算子、曲面拟合法等都是基于线性理论的，而采用线性理论的近似方法处理实际的非线性过程很容易丢失或模糊图像的细节部分。而且线性图像处理算法是基于数值分析和卷积运算，其抗干扰性和实时性不好，若要大幅度地提高图像处理速度它们就显得有点力不从心。因此，采用分形这种非线性的图像处理算法对焊接图像进行预处理。

目前对分形的相对完整的描述为：分形是对没有特征长度但具有某种意义下的自相似的形体和结构的总称。

分形可以分为规则分形和不规则分形。在分形名词使用之前，一些数学家就提出过不少复杂和不光滑的集合，如Cantor集、Koth曲线、Sierpinski垫片、地毯和海绵等。这些都属于规则的分形图形，它们具有严格的自相似性；而自然界的许多事物所具有的不光滑性和复杂性往往是随机的，如蜿蜒曲折的海岸线、变幻无穷的布朗运动等，这类曲线的自相似性是近似的或统计意义上的，这种自相似性只存在于标度不变区域（用于测量的尺子的标度变化时，被测的图形不会发生变化），超出标度不变区域，自相似性不复存在，这类曲线为不规则分形。

通常所说的维数指的是拓扑维数。拓扑学是研究可以连续变化的图形的学科，而几何学是研究刚性图形的学科。在几何学中圆和正方形是不同的，但在拓扑学中两者是等价的，因为它们可以连续地相互变换，并且都将平面上的点分成图形内、图形外和图形上的3个集合，所以它们具有共性。类似地，一条十分曲折但连续的折线和一条直线是等价的，因为它们可以连续地相互变换，而且两者的拓扑维数都是1。

上述规则分形符合豪斯道夫维数大于拓扑维数的定义。Cantor集是无限多点形成的点集，其总长度趋于0，按照拓扑学的图形可以连续地变形的概念，这个集可以无限地收缩，所以它的拓扑维数为0，而它的豪斯道夫维数为0.631；Koch线的长度趋向无穷大，但面积为零，它可以连续地拉成直线，所以它的拓扑维数为1，而它的豪斯道夫维数为1.269；Sierpinski三角形的面积趋于0，所以它的拓扑维数为1，而它的豪斯道夫维数为1.585。

规则分形的自相似性和标度不变性（无标度区间，简单地说就是自相似性存在的区间）是无限的（测度尺度可以趋于无限小）。不管怎样缩小或者放大标度去观察图形，其组成部分和原来的图形没有区别，也就是说它具有无限的膨胀和收缩相对性。当然，任何分形图形的标度应小于等于整个图形的尺寸，实际可以观察到的分形的最小组成部分也是有限的。

总结以上关于分形维数的特点，可以发现分形维数的D的基本性质：

1）分形维数D的大小反映了轮廓在空间的复杂不规则和充满空间的程度。D越大，细节越丰富；D越小，细节越少。

2）分形维数D与尺度无关。

3）分形维数D是一个相对量。

4）若集合A是欧氏空间的一个光滑（连续可微）的m维曲面，则分形维数D=m。

维数是几何对象的重要特征量，它是几何对象中一个点的位置所需要的独立坐标数目。在分形学里维数可以为分数，通过分形维数可以描述和测量分形的特征。在实际中，常用Richardson定律来估计分形维数：

式中 ε——尺度因子；

A（ε）——尺度ε下的度量特征值；

D——分形维数；

d——拓扑维数；

K——分形系数。

对于理想的均匀二维灰度图像，A（ε）为图像表面积测度，拓扑维数为2，则有A（ε）=Kε^2-D。对于分形维数，人们倾注了许多注意力，并指出分形维数是图像表面不规则程度的一种度量，它反映了图像灰度曲面的粗糙程度。

分形描述的不是几个像素间的灰度关系，而是相对较大区域内的所有像素的平均统计特性。在图像处理中引入分形理论，正是为了引入这种对图像相对宏观描述的方法。广义而言，任何物体表面都可以看做是由某种纹理特征的表面构成，故任何图像都是包含了若干纹理区域的灰度表面，而纹理特征的变化包含了图像的边缘信息。这些不同纹理灰度表面之间灰度起伏变化显著，外在就表现为边缘。Pentland通过对自然景物纹理图像的研究，证明了自然界中大多数物体表面影射成的灰度图像是具有相同分形特征的分形表面。且大多数自然景物的灰度图像是满足各向同性DFBR场模型的。既然图像表面统计特性满足各向同性的分数布朗随机场，而在不同的区域内分形特征参数H值会发生奇异转变，那么利用分形特征参数H值的奇异转变可以用作为图像的边缘检测。

选取一块N×N区域的图像区域，图像区域中某一点像素的灰度强度用F（x，y）表示，因为图像灰度场满足离散分数布朗随机场，因此有

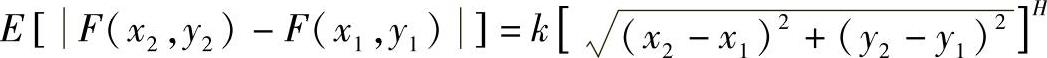
令

则有

等式两边取对数：

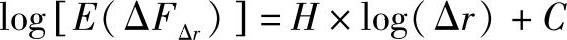
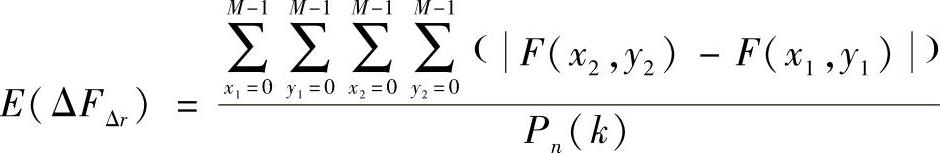
式中 H——分形维特征参数；

ΔF_Δr——图像区域中两像素点灰度值差的绝对值；

Δr——图像区域中所有可能的像素点对之间的距离；

P_n（k）——某一特定Δr距离的所有像素点对的数目；

C——常数。

这样，在图像区域中任意指定一个像素点对的距离，就能够得到一对数据（log[E（ΔF_Δr）]，log（Δr）），通过最小二乘法对图像区域中所有距离对应的数据进行拟合，就能够得到该图像区域中心像素的分形特征参数H。由于DFBR场具有自仿射分形特征，因而一定有0<H<1，而且Hurst指数H（0<H<1）越小，像素的表面越粗糙。但是图像若存在于不同的区域就破坏了DFBR场的一致性，因而会出现H值得奇数即H>1的情况。

由Hurst指数可以得到图像表面的分形维数D=D_T+1-H。其中D_T为图像表面的拓扑维数，由于拍摄到的图片为平面图像，故其拓扑维数为2，因此分形维数D=3-H。

采用3×3的模板，将模板自左到右、自上到下遍历整幅图片就可以得到整个图像中所有像素的分形维数，然后根据H值的奇异转变确定图像的边缘。在计算H参数时，模版不宜太大，如采用5×5的模板边缘检测的结果将遗漏较多的重要细节，一般取3×3的模板即可。

图5-3-27 TIG焊熔池图像边缘提取过程

a）原始图像 b）DFBR检测结果

图5-3-27所示为TIG焊熔池图像边缘提取的整个过程所得到的图片。图5-3-27a为熔池原始图像；图5-3-27b为运用分形中DFBR场理论通过分形特征参数H值的奇异转变提取到的图像边缘，由图可以看出熔池的边缘已经基本提取出来了。由此可见在对原始图像不进行预处理的情况下，分形理论中的DFBR场理论能够很好地提取到图像的边缘。

分形理论在焊接中的应用探析

相关推荐