小波分析理论及其在焊接中的应用

2023-06-26 理论教育版权反馈

【摘要】：小波变换是迄今为止最有效的信号分析方法，它在时频平面上，同时具有很好的时间和频率分辨能力，能够分辨多尺度特征信号的细节部分。小波变换在信号处理、计算机视觉等领域发挥越来越大的作用。小波分析兼具处理空间和频率信息的特点。小波分析在弧焊图像降噪、边缘特征信息提取、视觉跟踪等方面具有重大的潜在优势。

小波变换是法国工程师J.Morlet在1980年前后从事石油地质信号处理时，通过对加窗Fourier变换的改进而使用的分析工具。1984年他与理论物理学家A.Grossmann合作，基于物理直观构造了精确的小波变换反演公式，从而建立了连续小波变换（Continuous Wavelets Transform，CWT）的几何体系。它是基于仿射群（即伸缩/平移）下的不变性。1985年法国数学家Y.Meyer在看过J.Morlet等人的论文后，将小波变换与纯数学领域中的谐波分析联系起来，构造出具有很好的时间-频率局域特性的一维正交小波基。他的学生P.G.Lemarie把这一结果推广到n维的情形。1986年Y.Meyer与从事计算机视觉和图像分析的S.Mallat合作提出多尺度分析的概念，给出了构造小波基的一般方法。参照P.J.Burt和J.Crowley在信号处理中使用金字塔算法，S.Mallat提出了在正交小波基下信号分解的快速算法，即Mallat算法。1988年I.Daubechies证明了具有有限支集正交小波基的存在性，之后“适应基”小波包算法（WPT）、双正交样条小波理论及向量小波分析等理论大量涌现。

小波变换是迄今为止最有效的信号分析方法，它在时频平面上，同时具有很好的时间和频率分辨能力，能够分辨多尺度特征信号的细节部分。配合各种小波分解算法，如Mallat算法等，小波变换可用于图像降噪、特征信息提出、三维图像重建等方面。小波变换在信号处理、计算机视觉等领域发挥越来越大的作用。弧焊图像中含有丰富的空间和频率信息，一般的图像处理方法因缺乏有效的数学工具，有的只利用了统计信息或频率信息，没能充分地运用和处理图像的空间信息和频率信息。小波分析兼具处理空间和频率信息的特点。小波分析在弧焊图像降噪、边缘特征信息提取、视觉跟踪等方面具有重大的潜在优势。

对于含有大量噪声的弧焊图像信号，可用多分辨小波变换分解后所获得的小波系数来刻画，小波系数标明携载信号能量的权重，通过信号能量阈值法可达到降噪目的，其中以D.L.Donoho的软阈值降噪法效果最好。

小波变换的另一重要特性是用小波变换的模极大值表征信号的局部奇异性，由于小波变换有很好的时频定位功能，它不仅能检测出信号的奇异性，还能估计出奇异性大小，因此小波变换特别适于瞬变和突变信号分析。在图像信号中，突变部分如边缘和轮廓，携载重要的特征信息，采用多分辨小波变换的模极大值法可高效准确地进行边缘检测。弧焊图像的边缘特征提取是焊缝位置识别和预测熔池宽度的前提条件，而以往的边缘提取都是在原始图像上进行的，从小波多尺度的观点来看，这种边缘提取只是在一个尺度上进行的，不利于区分图像中的小结构轮廓和大结构边缘。利用小波变换技术进行弧焊图像的边缘提取，就产生了多尺度边缘，它是把原始图像分解，小波矢量的模局部极大值就对应着图像的边缘，在各个尺度上寻找模局部最大值来准确地确定弧焊图像的边缘特征。

利用小波变换的上述功能可对弧焊过程CCD视觉系统所获得的图像信息进行降噪处理、边缘检测，从而提取出焊炬与焊缝位置偏差信息、熔池宽度及形状信息，这些信息可分别用于焊缝自动跟踪和熔深的控制。

小波分析具有以下两个最大的特点：一是自适应性，它能根据分析对象自动调整有关参数；二是数学显微镜性质，它能根据观察的对象自动调焦，以取得最佳效果。实质上小波变换是一组高通、低通、带通滤波器组的组合，其滤波器具有自适应性，即分析检测高频分量时，时间窗口自动变窄、频率窗口增加；分析检测低频特性时，时间窗口自动变宽、频率窗口减少，或者说其滤波特性的品质因数Q恒为一常数，因而小波相当于一个恒Q滤波器。

小波分析是傅氏分析的重大突破，具有广泛的应用价值，有关小波的基本概念如下：设ϕ（t）为允许小波，其离散二进制小波函数族

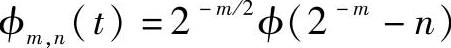
，即有

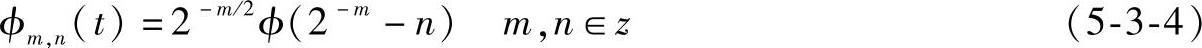
式中，m称为尺度参数，n称为平移参数。并设f（x）=L²（R），其离散小波变换定义为

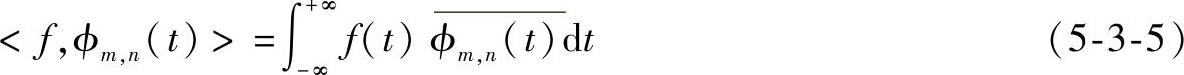
其意义如下：通过选取适应的放大倍数2^-m/2，在一个特定的位置研究一个函数或信号过程，然后平移到另一个位置继续研究。如放大倍数放大，也就是尺度变小，可按小步长移动一个距离，反之亦然。

作为小波变换须满足以下几个基本条件：

1）小波容许条件，即具有k阶消失矩：

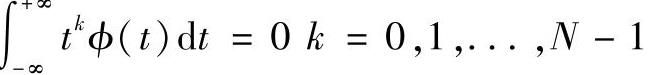
2）小波完全重构条件：

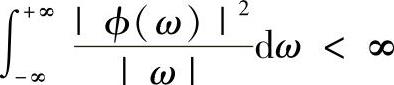
3）稳定性条件：

小波变换的多尺度分析设{V_j}是一给定多尺度分析，φ（t）和ϕ（t）分别是相应的尺度函数和小波函数。记：S₂_jf（t）=f（t）φ_2j（t）；W₂_jf（t）=f（t）ϕ_2j（t），则有

W_2jf（t）=W_2j-1f（t）G_j-1；S_2jf（t）=S_2j-1f（t）H_j-1 （5-3-6）

式（5-3-6）即为小波变换的快速算法[H和G分别是φ（t）和ϕ（t）对应的滤波器]，其结构框图如图5-3-23所示。

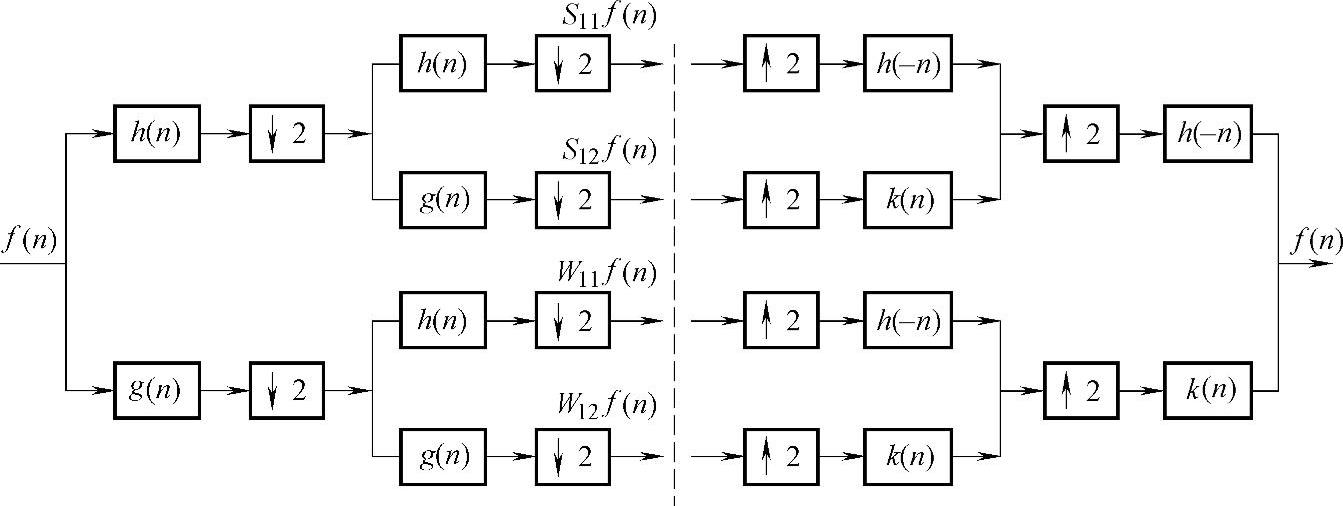
图5-3-23 结构框图

让离散的信号序列f（n）分别通过低通滤波器h（n）和高通滤波器g（n），就把f（n）分解为四个序列S₁₁f（n）、S₁₂f（n）和W₁₁f（n）、W₁₂f（n）。再把S₁₁f（n）、S₁₂f（n）和W₁₁f（n）、W₁₂f（n）通过低通滤波器h（-n）和高通滤波器k（n）从而实现信号的重构f（n）。↑2表示上采样，↓2表示下采样。

这些滤波器组应满足式（5-3-7）：

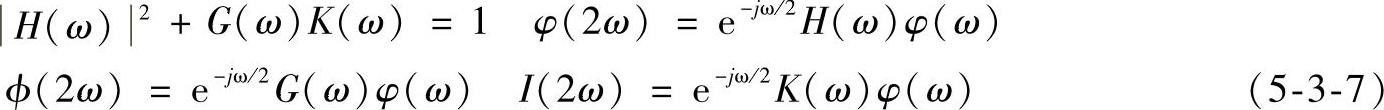
用数学表达式表示的信号处理过程如下：

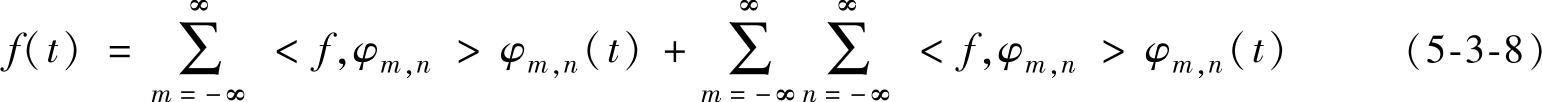
尺度函数φ（t）应满足：∫-∞∞φ（t）dt=1。式（5-3-8）右边的第一部分用于提取满变轮廓和边缘一类的特征；第二部分由小波函数用于在所有尺度上作细化处理。尺度因子m是根据信号性质和所要求的信息内容而事先选定的。Mallat在多尺度分析的基础上，给出了计算＜f，φ_m，n＞和＜f，ϕ_m，n＞的快速算法——Mallat算法。其算法优点是不需要知道φ（t）和φ（t）的解析式，且易于实现。

上述算法推广到二维的情形，在变换的每一层次，图像都被分解为4个1/4大小的图像，每一个都是由原图与一个小波基图像的内积后，再经过在x和y方向都进行2倍的间隔抽样而生成，这一过程就是二维多尺度分析。由于多尺度分析方法是在对图像进行多级分解的基础上进行逐级匹配，并且扩展了传统的视差定义，将两个限制条件：视差连续性和方向一致性融合进视差的定义当中，在视差求取的同时也完成了粗差剔除的过程，因而提高了效率。加上多尺度分解提供了不同尺度下图像的信息，并且变换后的能量大部分集中在低频部分，方便对不同尺度下的小波系数进行分类，有利于提取焊接图像的各种不同类型的边缘。

小波变换具有更为合理的子带多分辨分析与时频分析的框架，而且与滤波器组的构造具有一一对应的关系，这就为设计多滤波器组提供了一种方法。在结合各种不同的实际应用时，人们通常希望小波具有以下3个性质：

1）对称性：从视觉的角度而言，人们对不对称的误差比对对称性的误差更为敏感。

2）正交性：正交性能更好地去除信号的相关性，在提高图像的压缩比和复原图像方面应用比较多。

3）紧支撑；在实际应用中，因为计算上的需要，希望获得有限长滤波器，这就要求小波是紧支撑的。

小波变换为图像的边缘分析提供了新的手段，它把图像信号分解成呈现在不同尺度上的多个分量。尺度S描绘出通过小波变换所提取的图像信号特征。在不同尺度下，离散信号的全面描述取决于在尺度2 j时，对整数j研究下的小波变换的局部极大值。通过增加两个局部极大值点间“尺寸”，可以增加信号的信息分量。小波变换的局部极大值点刻画出了图像信号突变点的位置（图像边缘位置）。通过选择适当的小波函数，可以使小波分解的细节分量真实地反映出图像的局部灰度突变点。

边缘检测是图像处理中基础而又重要的课题。目前已有梯度算子、拉普拉斯算子、Robert算子、Sobel算子、Marr算子等众多方法。1992年，S.Mallat利用三阶中心B样条小波实现了多尺度边缘检测。从时频分析的角度对n阶B样条的性质进行了研究，认为三阶B样条在边缘提取中是渐近最优的。使用三阶中心B样条对图像进行平滑，然后用其一阶和二阶导数进行边缘检测。平滑的效果与所选取的B样条阶数，即与高斯函数的近似程度有关，但平滑函数的尺度不容易改变。Marr提出的边缘检测算子，首先使用高斯函数对原始图像作平滑，经拉普拉斯算子运算、再用提取零交叉点的方法作边缘检测。谢绍辉、吴立德在文献中研究了用作平滑作用的高斯函数中的σ对所提取的边缘及输出信噪比的影响。

计算机视觉通常采用“由粗到细”的搜索识别方法。为了实现快速搜索的目的，在不同的阶段，对所提取边缘细节程度的要求是不同的。为了实现观察距离“调焦”和所检测边缘细节程度选择，取高斯函数的一阶和二阶导数作为小波基，使用Mallat算法实现小波分解。小波分解的级数对应于观察距离“调焦”，改变高斯函数的标准差σ可选择所检测边缘的细节程度。由此实现了具有两个可变参数的多尺度边缘检测。

基于Mallat提出的小波模极大值边缘检测方法和多孔算法，采用B样条构造的小波基进行熔池边缘和焊缝位置检测的具体步骤如下：

1）先对图像f（x，y）进行预处理，得到S_2jf（x，y）。

2）对S₂f_j（x，y）先用行与h^j₀作卷积，再用列与h^j₀作卷积，求得S_2j+1f（x，y）。

3）用S_2j+1f（x，y）的每一行与h^j₁作卷积，求得W^y_2j+1f（x，y）。

4）用S_2j+1f（x，y）的每一列与h^j₁作卷积，求得W^y_2j+1f（x，y）。

5）用八邻域模版扫描图像，求出局部模极大值点swf（x，y）。

6）计算各点幅角，并规格化为图5-3-24所示的8个方向。

图5-3-24 八邻域模板

7）如果沿垂直于模极大值点幅角方向相邻两点的模小于该点，则认为该点是边缘点并标记。

8）设置阈值T=t%×max（swf（x，y）），滤除由于噪声和干扰生成的极值点。

9）对认定的边缘点重新设置灰度值。

10）对剩下的点用轮廓跟踪法连线，并对连线进行细化处理。

11）去除孤立点等。

12）在h^j₀和h^j₁系数间插入2^j-1个零。

13）重复步骤（2）到（12），直到j=J。

关于阈值T的选取问题，由于自适应阈值不仅难于定义，而且计算麻烦，效率很低，所以采用了一种保留t%的像素作为候选边缘像素的方法。使用参数t而不是用一个绝对的阈值，在选择时可以比较灵活，尤其是在边缘强度变化范围未知时，更是如此。

针对MAG焊熔池进行了试验研究。工艺试验条件如下：采用IGBT式逆变电源，焊接电流为120A，电压22V，送丝速度5mm/s，试件为2mm厚的Q235A钢板，采用对接焊缝。图像采集系统配置：PIV CPU，512M内存，Matrox Imaging Adapter，CCD摄像头。通过工艺试验，实时获得熔池图像，对比分析不同阈值和不同尺度对所获得图像边缘检测的影响。

在相同尺度下比较不同阈值的情况，其熔池边缘及焊缝位置检测结果如图5-3-25所示。从图中可见，随着所取阈值的减小，边缘明显粗化，定位精度受到影响，但边缘的连续性得到增强。综合对比阈值t=9.5较为合适。