钎焊时固态母材在液态钎料中的溶解过程是一个多相反应过程，它经历两个阶段。第一阶段是母材与钎料接触的表面层的溶解，这个反应发生在固-液两相界面上。而母材A在钎料B中的极限溶解度越大，则钎料成分达到饱和所需的时间就越短，消耗的母材的量越多，溶解量就越大。当液态钎料被母材溶质原子饱和后，溶解过程停止。......
2023-06-26
液态钎料的毛细填缝过程探析
【摘要】：钎焊时，对液态钎料的要求主要不是沿固态母材表面的自由铺展，而是填满钎缝的全部间隙。拉普拉斯方程为研究钎料的填缝过程提供了理论基础。由于间隙处于水平位置，液态钎料填缝时的附加压力与重力垂直，所以重力不起抵消附加压力的作用。
钎焊时，对液态钎料的要求主要不是沿固态母材表面的自由铺展，而是填满钎缝的全部间隙。通常钎缝间隙很小，如同毛细管，钎料是依靠毛细作用在钎缝间隙内流动的。因此，钎料能否填满钎缝间隙取决于它在母材间隙中的毛细流动特性。拉普拉斯方程是有关流体界面的基本公式，是对许多界面现象作出定量解释的基础。拉普拉斯方程为研究钎料的填缝过程提供了理论基础。
1.液态钎料在垂直平行板中的填充特性
当将两互相平行的金属板垂直插入液态钎料中时，假设平行金属板无限大，钎料量无限多。由于存在毛细作用，如果钎料可以润湿金属板，则液态钎料会自动上升到高于液面的一定高度；若钎料不润湿金属板，则液态钎料将下降到低于液面的一定高度。由于液面弯曲产生附加压力，导致液面上升或下降，因此可用拉普拉斯方程来求解最大上升高度及爬升速度。
（1）最大上升高度 当平行板所构成的间隙为a，弯曲液面的曲率半径为R1→∞，R2=a/2，则a=-2Rcosθ，根据拉普拉斯方程，液面两侧的压力差为
当θ<90°时，cosθ是正的，Δp为负，液面下液相压力小于气相压力，平衡时液面必上升h，以达到
式中 ρ——液体的密度，单位为g/cm3；
g——重力加速度，单位为m/s2。
此时最大爬升高度为
将杨氏方程代入式（3-1-19），可得
由式（3-1-19）和式（3-1-20）可见：当θ<90°时，cosθ>0，即在钎料润湿母材时，h>0，液态钎料沿间隙上升；当θ>90°时，cosθ<0，即钎料不润湿母材，h<0，液态钎料沿间隙下降。因此，钎料填充间隙的好坏取决于它对母材的润湿性。此外，钎料沿间隙上升的高度h与间隙大小a成反比。从上升高度来看，设计钎焊接头时，接头间隙应尽量小些。
（2）爬升速度 由于凹的弯液面对液体产生一个负的压力，液面在任一位置y的上升的驱动力应为负的附加压力与重力产生的压力差，即
根据泊肃叶（Poiseuille）定律可知：不可压缩牛顿流体在圆管中作定常层流时，体积流量正比于比压降和管半径的四次方，反比于流体的粘度，即
流体在圆管断面上的平均速度可表示为
将式（3-1-21）代入式（3-1-23），可得液面在任一爬升高度时的爬升速度为
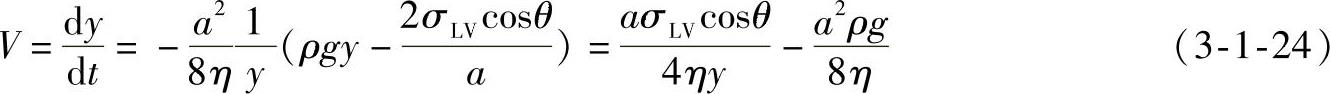
当y很小，a也很小时，式（3-1-24）的第二项可以忽略，于是可简化成
从式（3-1-25）可以看出，钎料润湿性越好，钎料的流动速度越大；液体的粘度越大，流速越小；母材间隙越大，填缝速度越快。其次，钎料的爬升速度和爬升高度成反比，即液体在间隙内刚开始上升时流动快，以后随高度的增加而逐渐变慢。这一性质对钎焊接头设计及钎焊工艺优化有指导意义。
2.液态钎料在水平平行板中的填充特性
液态钎料在水平位置平行间隙中的填缝更接近于实际的钎焊情况。由于间隙处于水平位置，液态钎料填缝时的附加压力与重力垂直，所以重力不起抵消附加压力的作用。
当液态钎料润湿母材时，钎料填缝的附加压力为
根据泊肃叶流速方程，可得水平平行板的填缝速度为
积分后得填缝长度和填缝时间的关系为
从式（3-1-27）和式（3-1-28）可以看出，在考虑钎料润湿母材的条件下，间隙越大、粘度越小，钎料的填充速度越快。在刚开始填充时的流动速度最大，而后呈反比递减。其次，填缝长度和填缝时间呈抛物线规律变化。如果钎料无限多，填缝过程可以一直进行下去。这在实际钎焊过程中是不可能出现的，因为在实际钎焊过程中，母材和熔化的钎料之间有相互作用，致使粘度变化，钎缝中的缺陷也会阻碍钎料的流动。
3.单板垂直插入液态钎料时的润湿特性
单板垂直插入液态钎料试验方法又称为吊片法，是Wil- helmy在1863年首先提出的。该方法被广泛应用于软钎焊润湿性和钎焊性评估（图3-1-5）。当垂直的金属板插入液态钎料槽时，如果液态钎料润湿金属板，则润湿的弯月面在液面上方上升一段距离h，这个弯月面对金属板施加一个向下的、等于弯月面重量的力。正是这个表面弯曲产生的附加压力，引起液面的上升。
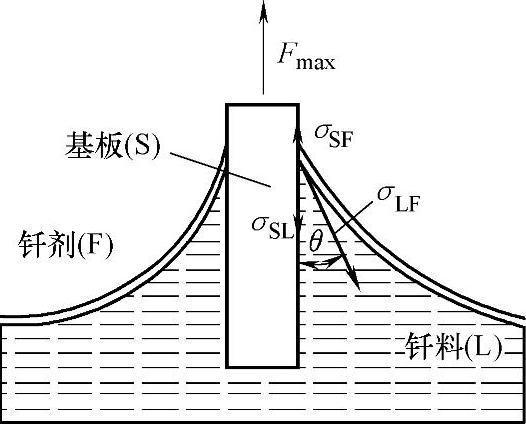
图3-1-5 润湿垂直板的弯液面形状
假设液态钎料无限多，液体体积在试验过程中是不变的，根据Goodrich考虑整个毛细系统的势能为每单位深度的能量积分，可得
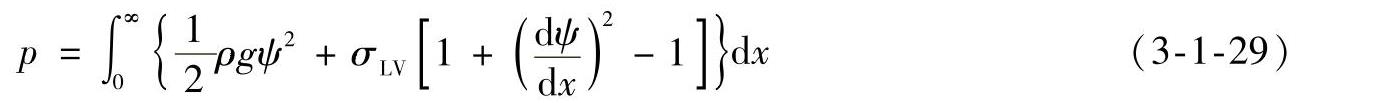
Y=Ψ（x）为弯月面形状函数，联立的Euler-Lagrange方程为
满足式（3-1-30）的弯月面的形状函数为：
因此，满足毛细升高的固-液-气三点线（TPL）到液面的高度为
平衡时的最大润湿力（或弯月面的重量，W）可由式（3-1-33）给出（图3-1-5）：
F=W=σLVLcosθ （3-1-33）
式中 L——铜板浸入液态钎料的周线长度（mm）。
通过测量最大润湿力F和润湿高度h，联立方程（3-1-32）和方程（3-1-33），可以求出系统的表面张力和平衡润湿角如下：
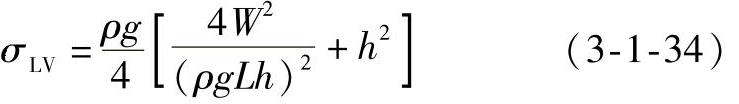
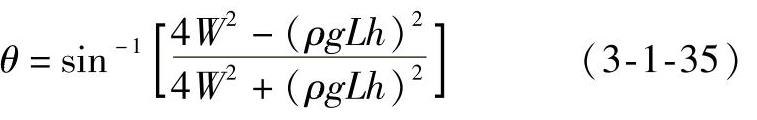
另一方面，通过Wilhelmy法，还可以连续测量润湿力。在金属板刚接触钎料液面的时候，浮力大于润湿力，一旦润湿开始，润湿力快速提拉弯月面到金属板上，直到平衡建立。典型的润湿力—时间曲线如图3-1-6所示。通过润湿力和润湿时间的比较，可以对系统的润湿性及钎焊性进行定性的评估。如果能对爬升高度和润湿角实时检测，则可对系统的润湿动力学进行研究（即随时间变化的三点线的运动轨迹和润湿角的变化规律）。
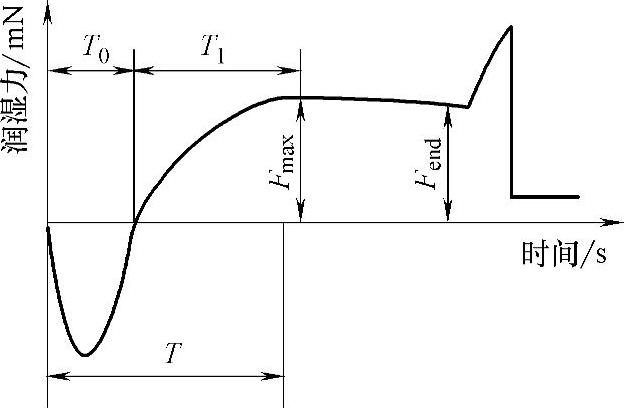
图3-1-6 润湿力随润湿时间变化曲线示意图
有关焊接方法与过程控制基础的文章
- 详细阅读
-
液态钎料润湿固体母材的效果分析详细阅读
由于固体的表面亥姆霍兹自由能、固-液界面亥姆霍兹自由能尚无合适的测定方法，但通过接触角，即可判断一种液体对固体的润湿性。杨氏方程虽然可以对钎焊过程进行近似的描述，杨氏方程也可以从能量和力学的角度在平衡条件下推导，但必须指出的是，在钎焊过程中，液态钎料和固态母材界面会发生相互作用，在这种情况下进行的表面润湿、铺展就更为复杂。4）在液态钎料组元和母材组元之间的化学反应。......
2023-06-26
-
钎料分类和性能简介详细阅读
常用的钎料一般根据熔点分成两类。熔点高于950℃的常称为高温钎料。另一类是软钎料，熔点在450℃以下，应用最广泛的软钎料是锡基钎料，多数软钎料适合的焊接温度为200～400℃，通常把用这类钎料进行的钎焊称为软钎焊。软钎焊接头强度较低，适于受力不大或工作温度较低的焊件，典型的就是电子产业中的应用。......
2023-06-26
-
如何选择镍基钎料？详细阅读
当要求钎焊件在更高温度下工作时可以采用镍基钎料。镍基钎料以镍为基体，并添加了能降低熔点及提高其热强度的元素。因此镍基钎料通常是以粉状、粘带和非晶态箔供应的。镍基钎料钎焊不锈钢时的一个重要特征是钎焊接头性能对接头间隙值极为敏感。镍基钎料适用于炉中钎焊、感应钎焊和电阻钎焊等工艺方法。镍基钎料的化学成分应符合表3-3-22的规定。表3-3-21 镍基钎料的分类、型号和钎焊参考温度表3-3-22 镍基钎料的化学成分......
2023-06-26
-
钎料润湿性影响因素分析详细阅读
由杨氏方程可知，任何使三相表面张力发生变化，从而使接触角θ发生变化（减少）的因素都将影响钎料对母材的润湿性。从物理意义上说，如使σLV减小，意味着液体内部原子对表面原子的吸引力减弱，液体原子容易克服本身受到的引力趋向液体表面，使液体的表面积增大，钎料容易铺展。而σSV增大，说明固体的内部原子对表面原子的吸引力增大，表面原子处于高能态。......
2023-06-26
-
钎料和母材成分分析详细阅读
图3-1-7 Fe-Ag二元合金相图大量研究表明，钎料和母材的成分对润湿性的影响主要表现为钎焊过程中的液态钎料和固态母材是否有相互作用。其规律性可表述为钎料和母材在液态和固态均不相互作用，则它们的润湿性很差；若钎料和母材能相互溶解或形成化合物，则液态钎料能较好地润湿母材。从以上分析可知，对于那些与母材无相互作用因而润湿性差的钎料，通过在钎料中加入能与母材形成共同相的合金元素，可以改善它对母材的润湿性。......
2023-06-26
-
Sn-Pb系钎料的特点及应用详细阅读
Sn-Pb钎料的应用有几千年的历史，是电子封装行业中应用最为成熟的钎料。图3-4-3为Sn-Pb二元合金相图。共晶成分Sn为61.9%、Pb为38.1%，共晶温度为183℃，共晶体由体心正方的β-Sn相和面心立方的α-Pb相组成。这还要从钎焊性能、成本因素等多方面综合考虑，因此一般在电子组装行业，生产实际应用最多的还是把共晶点附近成分的Sn-Pb合金作为钎料。......
2023-06-26
-
银基钎料的分类、型号及成分说明详细阅读
为了避免出现脆性，银铜锡钎料中锡的质量分数一般不高于10%。为了进一步降低银钎料的熔化温度，可在银铜锌合金中加入镉。银基钎料适用于气体火焰钎焊、电阻钎焊、炉中钎焊、感应钎焊和浸渍钎焊等工艺方法，用途较广泛。根据GB 10046—2008《银基钎料》标准规定，银基钎料的分类、型号、成分及熔化温度见表3-3-14。表3-3-14 银钎料的分类、型号、化学成分及熔化温度（续）（续）注：1.单值均为最大值，“余量”表示100%与其余元素质量分数总和的差值。......
2023-06-26
相关推荐